例1：合并有序顺序表

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

  设计实现一个时间复杂度为 O(m + n) 的算法解决此问题.

解：对于这道题来说我们有多种思路，但是在限制了时间复杂度后，三变量就是最好的方法。

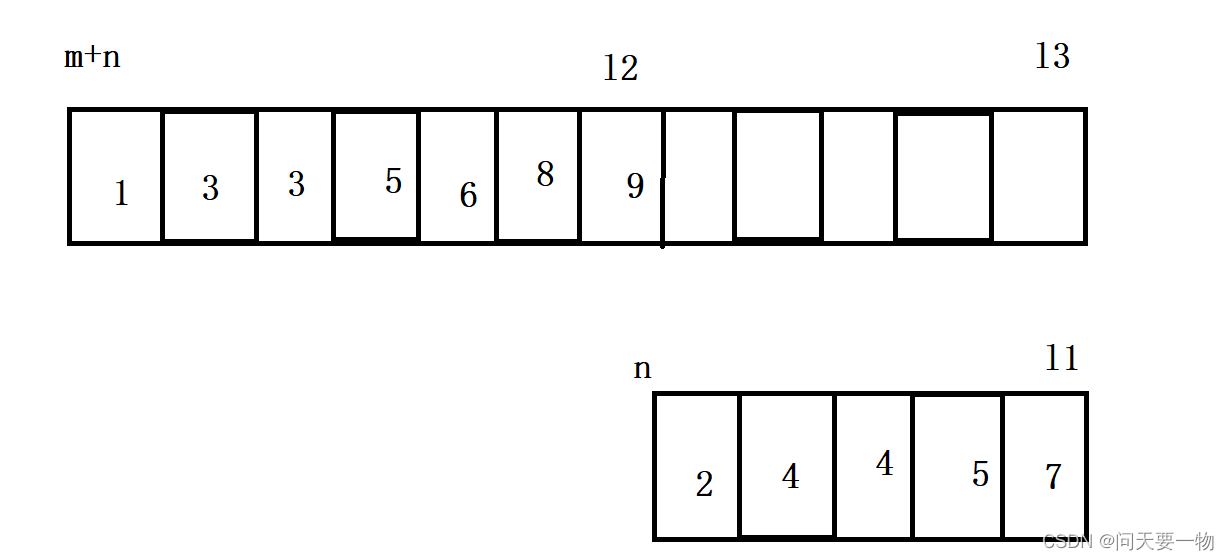
        我们常见三个变量l1、l2、l3，然后对l2和l1数组中的元素进行比较，大的数存储到 l3 中，随后l3和放置数到l3位置的变量都向前一个位置，即-1。当l2或者l1先走到尽头的时候，我们只要把剩余的元素按顺序放到nums1中就完成了合并。代码如下：

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) 
{
    int l1,l2,l3;
    l1 = m-1;
    l2 = n-1;
    l3 = m+n-1;    
    while(l1 >= 0 && l2 >= 0)
    {
        if(nums1[l1] > nums2[l2])
        {
            nums1[l3] = nums1[l1];
            l1--;
            l3--;
        }
        else
        {
            nums1[l3] = nums2[l2];
            l2--;
            l3--;
        }
    }
//注意，因为l1本来就在nums1中，所以不许重新放置，只考虑l2就可以了。
    while(l2 >= 0)
    {
        nums1[l3] = nums2[l2];
        l2--;
        l3--;
    }
}

例2：移除元素

        给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

       说明:

        为什么返回数值是整数，但输出的答案是数组呢?请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

 解：这道题的解题思路比较简单，但是很新颖。我们设置两个整型变量(src、dest)并初始化为0，然后src用来遍历数组，dest是当src遍历到的数组元素不为val值时，赋值给dest并向后一个位置。

这样在遍历结束时，dest的值也正好是返回值。代码如下：

int removeElement(int* nums, int numsSize, int val) 
{
    int src = 0;
    int dest = 0;
    for(int i=0;i<numsSize; i++)
    {
        if(val == nums[i])
        {
            src++;
        }
        else
        {
            nums[dest++] = nums[src++];
        }
    }
    return dest;
}