数据结构与算法---树

news2025/1/9 14:48:44

数据结构可视化网址

  • Structure Visualization: https://www.cs.usfca.edu/~galles/visualization/
  • Totuma: https://www.totuma.cn/
  • Algorithm Visualizer: https://algorithm-visualizer.org/

构建二叉树

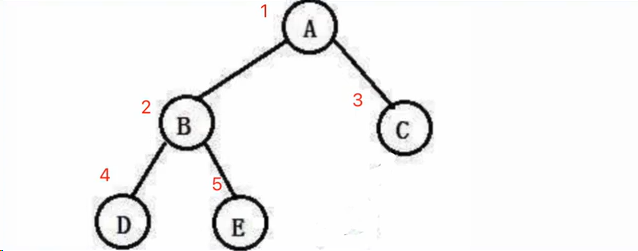
在这里插入图片描述

// C

#include<stdio.h>
#include<stdlib.h>

typedef char T;


typedef struct TreeNode {
	T data;
	struct TreeNode* left;
	struct TreeNode* right;
}Node;


int main()
{
	int spaceSize = sizeof(Node);

	Node* a = (Node*)malloc(spaceSize);
	Node* b = (Node*)malloc(spaceSize);
	Node* c = (Node*)malloc(spaceSize);
	Node* d = (Node*)malloc(spaceSize);
	Node* e = (Node*)malloc(spaceSize);

	a->data = 'A';
	b->data = 'B';
	c->data = 'C';
	d->data = 'D';
	e->data = 'E';

	a->left = b;
	a->right = c;
	b->left = d;
	b->right = e;
	c->left = c->right = NULL;
	d->left = d->right = NULL;
	e->left = e->right = NULL;
	
	free(a);
	free(b);
	free(c);
	free(d);
	free(e);

	getchar();
	return 0;
}

遍历二叉树

0.基本概念

二叉树是一种特殊的树形数据结构，其中每个节点最多有两个子节点，通常称为左子节点和右子节点。

当我们遍历二叉树时，可以根据访问节点的顺序得到不同的遍历结果。

有以下四种遍历方式：

  1. 前序遍历
    • 访问根节点
    • 前序遍历左子树
    • 前序遍历右子树
    • 对于给定的二叉树，前序遍历的结果是一个节点序列，这个序列首先列出根节点，然后递归地列出左子树的所有节点，最后递归地列出右子树的所有节点
  2. 中序遍历
    • 中序遍历左子树
    • 访问根节点
    • 中序遍历右子树
    • 在二叉搜索树（BST）中，中序遍历的结果是一个有序的节点序列，因为它首先遍历最小的节点（在BST的左下方），然后遍历根节点，最后遍历最大的节点（在BST的右上方）
  3. 后序遍历
    • 后序遍历左子树
    • 后序遍历右子树
    • 访问根节点
    • 后序遍历的结果是一个节点序列，这个序列首先列出左子树的所有节点，然后列出右子树的所有节点，最后列出根节点
  4. 层序遍历
    • 从根节点开始
    • 访问当前层的所有节点
    • 对下一层的每个节点进行同样的操作
    • 层序遍历通常使用队列来实现，首先将根节点入，然后在循环中，出队一个节点并访问它，然后将它的子节点（如果存在）入队。这个过程一直持续到队列为空

1.前序遍历

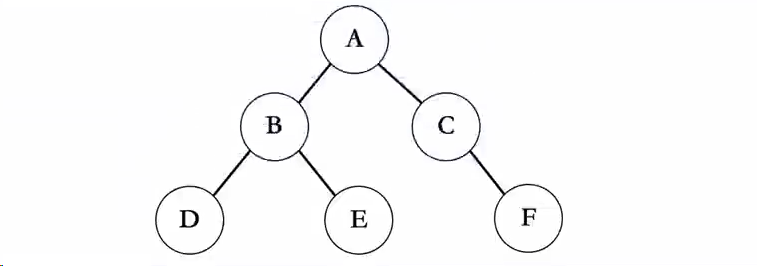
在这里插入图片描述

  • 通过递归的方式实现
// C

#include<stdio.h>
#include<stdlib.h>

typedef char T;


typedef struct TreeNode {
	T data;
	struct TreeNode* left;
	struct TreeNode* right;
}Node;


// 先序遍历
void preorder(Node* root)	// 参数：二叉树的根节点
{
	if (root == NULL)	return;
	printf("%c", root->data);
	preorder(root->left);
	preorder(root->right);
}


int main()
{
	int spaceSize = sizeof(Node);

	Node* a = (Node*)malloc(spaceSize);
	Node* b = (Node*)malloc(spaceSize);
	Node* c = (Node*)malloc(spaceSize);
	Node* d = (Node*)malloc(spaceSize);
	Node* e = (Node*)malloc(spaceSize);
	Node* f = (Node*)malloc(spaceSize);

	a->data = 'A';
	b->data = 'B';
	c->data = 'C';
	d->data = 'D';
	e->data = 'E';
	f->data = 'F';

	a->left = b;
	a->right = c;
	b->left = d;
	b->right = e;
	c->right = f;
	c->left = d->left = d->right = e->left = e->right = f->left = f->right = NULL;

	preorder(a);

	free(a);
	free(b);
	free(c);
	free(d);
	free(e);


	getchar();
	return 0;
}
  • 通过"循环+栈"的方式实现
// C

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

// 二叉树的节点
typedef char T;
typedef struct TreeNode {
	T data;
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;


// 栈的节点
typedef struct StackNode {
	TreeNode* node;
	StackNode* next;
}StackNode;


// 栈的初始化
void initStack(StackNode* head)
{
	head->next = NULL;
}


// 入栈
bool pushStack(StackNode* head, TreeNode* node)
{
	StackNode* p = (StackNode*)malloc(sizeof(StackNode));
	if (p == NULL)	return false;

	p->node = node;
	p->next = head->next;
	head->next = p;

	return true;
}


// 出栈
TreeNode* popStack(StackNode* head)
{
	StackNode* temp = head->next;
	TreeNode* node = head->next->node;

	head->next = head->next->next;
	free(temp);

	return node;
}


// 栈是否为空
bool isEmpty(StackNode* head)
{
	return head->next == NULL;
}


// 先序遍历
void preorder(TreeNode* root)
{
	StackNode stack;		// 创建一个栈
	initStack(&stack);		// 初始化这个栈

	while (root || !isEmpty(&stack))		// 如果栈不为空，也会继续循环下去
	{
		// 先不断遍历左子树，直到没有为止
		while (root)
		{
			printf("%c", root->data);
			pushStack(&stack, root);		// 途中每经过一个节点，就将节点丢进栈中
			root = root->left;
		}

		// 处理右子树
		root = popStack(&stack);
		root = root->right;
	}
}

int main()
{
	int spaceSize = sizeof(TreeNode);

	TreeNode* a = (TreeNode*)malloc(spaceSize);
	TreeNode* b = (TreeNode*)malloc(spaceSize);
	TreeNode* c = (TreeNode*)malloc(spaceSize);
	TreeNode* d = (TreeNode*)malloc(spaceSize);
	TreeNode* e = (TreeNode*)malloc(spaceSize);
	TreeNode* f = (TreeNode*)malloc(spaceSize);

	a->data = 'A';
	b->data = 'B';
	c->data = 'C';
	d->data = 'D';
	e->data = 'E';
	f->data = 'F';

	a->left = b;
	a->right = c;
	b->left = d;
	b->right = e;
	c->right = f;
	c->left = d->left = d->right = e->left = e->right = f->left = f->right = NULL;

	preorder(a);	// 先序遍历

	free(a);
	free(b);
	free(c);
	free(d);
	free(e);


	getchar();
	return 0;
}

2.中序遍历

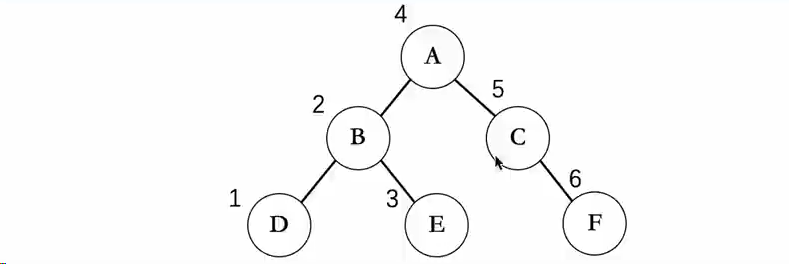
在这里插入图片描述

  • 通过递归的方式实现
// C

// 中序遍历
void inOrder(TreeNode* root)
{
	if (root == NULL) return;
	inOrder(root->left);		// 先完成全部左子树的遍历
	printf("%c", root->data);   // 等待左子树遍历完成之后再打印
	inOrder(root->right);		// 然后就是对右子树进行遍历
}
  • 通过"循环+栈"的方式实现
// C

// 中序遍历
void inOrder(TreeNode* root)
{
	StackNode stack;		// 创建一个栈
	initStack(&stack);		// 初始化这个栈

	while (root || !isEmpty(&stack))		// 如果栈不为空，也会继续循环下去
	{
		while (root)
		{
			pushStack(&stack, root);
			root = root->left;
		}
		root = popStack(&stack);
		printf("%c", root->data);   // 只需要将打印时机延后到左子树遍历完成
		root = root->right;
	}
}

3.后序遍历

// C

// 后序遍历
void postOrder(Node root){
    if(root == NULL) return;
    postOrder(root->left);
    postOrder(root->right);
    printf("%c", root->data);   // 时机延迟到最后
}

4.层序遍历

// C

#include<stdio.h>
#include<stdlib.h>

typedef char E;


// 树的节点
struct TreeNode {
	E element;
	struct TreeNode* left;
	struct TreeNode* right;
	int flag;
};
typedef struct TreeNode* Node;


// 队列的节点
struct QueueNode {
	Node element;
	struct QueueNode* next;
};
typedef struct QueueNode* QNode;


// 队列
struct Queue {
	QNode front, rear;
};


// 初始化
bool initQueue(Queue* queue) {
	QNode node = (QNode)malloc(sizeof(struct QueueNode));
	if (node == NULL)   return false;

	queue->front = queue->rear = node;

	return true;
}


// 入队
bool offerQueue(Queue* queue, Node element) {
	QNode node = (QNode)malloc(sizeof(struct QueueNode));
	if (node == NULL) return false;

	node->element = element;
	queue->rear->next = node;
	queue->rear = node;

	return true;
}


// 出队
Node pollQueue(Queue* queue) {
	Node e = queue->front->next->element;
	QNode node = queue->front->next;

	queue->front->next = queue->front->next->next;
	if (queue->rear == node) queue->rear = queue->front;
	free(node);

	return e;
}


// 判断是否为空
bool isEmpty(Queue* queue) {
	return queue->front == queue->rear;
}


// 层序遍历
void levelOrder(Node root) {
	struct Queue queue;		// 创建一个队列
	initQueue(&queue);		// 初始化这个队列

	offerQueue(&queue, root);		// 先把根节点入队
	while (!isEmpty(&queue))		// 不断重复，直到队列空为止
	{
		Node node = pollQueue(&queue);		// 出队一个元素，打印值
		printf("%c", node->element);
		if (node->left)		// 如果存在左右孩子的话
			offerQueue(&queue, node->left);		// 记得将左右孩子入队，注意顺序，先左后右
		if (node->right)
			offerQueue(&queue, node->right);
	}
}


int main()
{
	int spaceSize = sizeof(TreeNode);

	TreeNode* a = (TreeNode*)malloc(spaceSize);
	TreeNode* b = (TreeNode*)malloc(spaceSize);
	TreeNode* c = (TreeNode*)malloc(spaceSize);
	TreeNode* d = (TreeNode*)malloc(spaceSize);
	TreeNode* e = (TreeNode*)malloc(spaceSize);
	TreeNode* f = (TreeNode*)malloc(spaceSize);

	a->element = 'A';
	b->element = 'B';
	c->element = 'C';
	d->element = 'D';
	e->element = 'E';
	f->element = 'F';

	a->left = b;
	a->right = c;
	b->left = d;
	b->right = e;
	c->right = f;
	c->left = d->left = d->right = e->left = e->right = f->left = f->right = NULL;

	levelOrder(a);	// 层序遍历

	free(a);
	free(b);
	free(c);
	free(d);
	free(e);


	getchar();
	return 0;
}

线索化二叉树

线索化概念

一棵二叉树的某些结点会存在NULL的情况，我们可以利用这些为NULL的指针，将其线索化为某一种顺序遍历的指向下一个按顺序的结点的指针，经过第一次遍历完成了线索化，以后我们再进行遍历的时候，就可以利用线索实现快速遍历。

  • 一棵经过线索化以后的二叉树的前序遍历顺序如下：

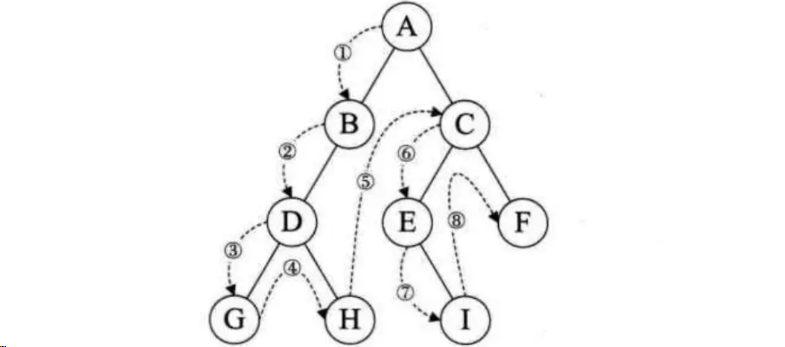
在这里插入图片描述

  • 一棵经过线索化以后的二叉树的中序遍历顺序如下：

在这里插入图片描述

  • 一棵经过线索化以后的二叉树的后序遍历顺序如下：

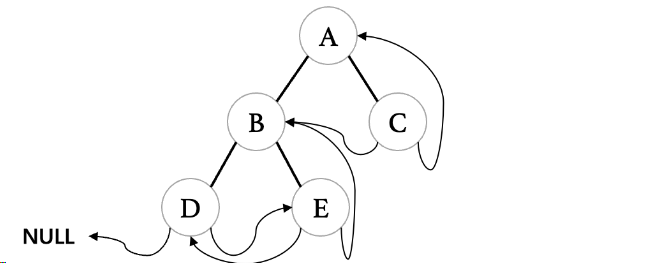
在这里插入图片描述

线索化规则

线索化的规则为：

  • 结点的左指针，指向其当前遍历顺序的前驱结点。
  • 结点的右指针，指向其当前遍历顺序的后继结点。

代码实现

// C

#include<stdio.h>
#include<stdlib.h>

typedef char E;

// 树节点
typedef struct TreeNode {
	E element;
	struct TreeNode* left;
	struct TreeNode* right;
	struct TreeNode* parent;	// 指向双亲（父）结点 ------ 只是"后序遍历"需要用这个属性
	int leftTag, rightTag;		// 标志位，如果为1表示这一边指针指向的是线索，不为1就是正常的孩子结点
} *Node;


// 创建结点
Node createNode(E element) {
	Node node = (Node)malloc(sizeof(struct TreeNode));
	node->left = node->right = NULL;
	node->rightTag = node->leftTag = 0;
	node->element = element;
	return node;
}


// "前序遍历"线索化函数
Node pre1 = NULL;  // 这里我们需要一个pre1来保存后续结点的指向
void preOrderThreaded(Node root) {
	if (root == NULL) return;

	if (root->left == NULL) {   // 首先判断当前结点左边是否为NULL，如果是，那么指向上一个结点
		root->left = pre1;
		root->leftTag = 1;  // 记得修改标记
	}
	if (pre1 && pre1->right == NULL) {  // 然后是判断上一个结点的右边是否为NULL，如果是那么进行线索化，指向当前结点
		pre1->right = root;
		pre1->rightTag = 1;  // 记得修改标记
	}

	pre1 = root;   // 每遍历完一个，需要更新一下pre1，表示上一个遍历的结点

	if (root->leftTag == 0)   // 注意只有标志位是0才可以继续向下，否则就是线索了
		preOrderThreaded(root->left);
	if (root->rightTag == 0)
		preOrderThreaded(root->right);
}


// "前序遍历"一棵经过线索化的二叉树
void preOrder(Node root) {
	while (root) {
		printf("%c", root->element);   // 因为是前序遍历，所以直接按顺序打印就行了
		if (root->leftTag == 0)
			root = root->left;   // 如果是左孩子，那么就走左边
		else
			root = root->right;   // 如果左边指向的不是孩子，而是线索，那么就直接走右边，因为右边无论是线索还是孩子，都要往这边走了
	}
}


// "中序遍历"线索化函数
Node pre2 = NULL;  // 这里我们需要一个pre2来保存后续结点的指向
void inOrderThreaded(Node root) {
	if (root == NULL) return;
	if (root->leftTag == 0)
		inOrderThreaded(root->left);

	// ----------线索化 ---------
	if (root->left == NULL) {
		root->left = pre2;
		root->leftTag = 1;
	}
	if (pre2 && pre2->right == NULL) {
		pre2->right = root;
		pre2->rightTag = 1;
	}
	pre2 = root;
	// ----------线索化 ---------

	if (root->rightTag == 0)
		inOrderThreaded(root->right);
}


// "中序遍历"一棵经过线索化的二叉树
void inOrder(Node root) {

	while (root) {   // 因为中序遍历需要先完成左边，所以说要先走到最左边才行

		while (root && root->leftTag == 0)    // 如果左边一直都不是线索，那么就一直往左找，直到找到一个左边是线索的为止，表示到头了
			root = root->left;

		printf("%c", root->element);   // 到最左边了再打印，中序开始

		while (root && root->rightTag == 1) {   // 打印完就该右边了，右边如果是线索化之后的结果，表示是下一个结点，那么就一路向前，直到不是为止
			root = root->right;
			printf("%c", root->element);   // 注意按着线索往下就是中序的结果，所以说沿途需要打印
		}
		root = root->right;  // 最后继续从右结点开始，重复上述操作

	}
}


// "后序遍历"线索化函数
Node pre3 = NULL;  // 这里我们需要一个pre3来保存后续结点的指向
void postOrderThreaded(Node root) {

	if (root == NULL) return;
	if (root->leftTag == 0) {
		postOrderThreaded(root->left);
		if (root->left) root->left->parent = root;  // 左边完事之后，如果不为空，那么就设定父子关系
	}
	if (root->rightTag == 0) {
		postOrderThreaded(root->right);
		if (root->right) root->right->parent = root;   // 右边完事之后，如果不为空，那么就设定父子关系
	}

	// ------ 线索化 -------
	if (root->left == NULL) {
		root->left = pre3;
		root->leftTag = 1;
	}
	if (pre3 && pre3->right == NULL) {
		pre3->right = root;
		pre3->rightTag = 1;
	}
	pre3 = root;
	// ------ 线索化 -------
}


// "后序遍历"一棵经过线索化的二叉树
void postOrder(Node root) {

	Node last = NULL, node = root;  // 这里需要两个暂存指针，一个记录上一次遍历的结点，还有一个从root开始
	while (node) {
		while (node->left != last && node->leftTag == 0)    // 依然是从整棵树最左边结点开始，和前面一样，只不过这里加入了防无限循环机制，看到下面就知道了
			node = node->left;
		while (node && node->rightTag == 1) {   // 左边完了还有右边，如果右边是线索，那么直接一路向前，也是跟前面一样的
			printf("%c", node->element);   // 沿途打印
			last = node;
			node = node->right;
		}
		if (node == root && node->right == last) {
			// 上面的操作完成之后，那么当前结点左右就结束了，此时就要去寻找其兄弟结点了，我们可以
			// 直接通过parent拿到兄弟结点，但是如果当前结点是根结点，需要特殊处理，因为根结点没有父结点了
			printf("%c", node->element);
			return;   // 根节点一定是最后一个，所以说直接返回就完事
		}
		while (node && node->right == last) {    // 如果当前结点的右孩子就是上一个遍历的结点，那么一直向前就行
			printf("%c", node->element);   // 直接打印当前结点
			last = node;
			node = node->parent;
		}
		// 到这里只有一种情况了，是从左子树上来的，那么当前结点的右边要么是线索要么是右子树，所以直接向右就完事
		if (node && node->rightTag == 0) {  // 如果不是线索，那就先走右边，如果是，等到下一轮再说
			node = node->right;
		}
	}
}





int main() {
	// 一颗二叉树的所有节点
	Node a = createNode('A');
	Node b = createNode('B');
	Node c = createNode('C');
	Node d = createNode('D');
	Node e = createNode('E');

	// 节点相连，形成二叉树
	a->left = b;
	b->left = d;
	a->right = c;
	b->right = e;

	// 前序遍历
	preOrderThreaded(a);	// 线索化
	preOrder(a);			// 遍历

	// 中序遍历
	inOrderThreaded(a);		// 线索化
	inOrder(a);				// 遍历

	// 后序遍历
	postOrderThreaded(a);	// 线索化
	postOrder(a);			// 遍历

	// 释放内存空间
	free(a);
	free(b);
	free(c);
	free(d);
	free(e);

	// 程序暂停
	getchar();

	// 结束主函数
	return 0;
}

二叉查找树

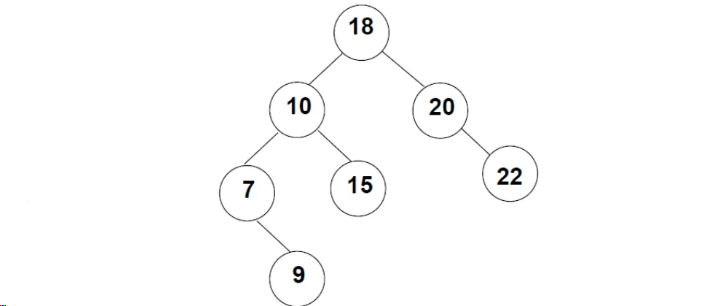
二叉查找树也叫二叉搜索树或是二叉排序树，它具有一定的规则：

  • 左子树中所有结点的值，均小于其根结点的值
  • 右子树中所有结点的值，均大于其根结点的值
  • 二叉搜索树的子树也是二叉搜索树

在这里插入图片描述

平衡二叉树

  • 动画演示：https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
  • 部分代码：
#include<stdio.h>
#include<stdlib.h>

typedef int E;

typedef struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
    int height;   // 每个结点需要记录当前子树的高度，便于计算平衡因子
} * Node;


Node createNode(E element){
    Node node = malloc(sizeof(struct TreeNode));
    node->left = node->right = NULL;
    node->element = element;
    node->height = 1;   // 初始化时，高度写为1就可以了
    return node;
}


int max(int a, int b){
    return a > b ? a : b;
}


int getHeight(Node root){
    if(root == NULL) return 0;
    return root->height;
}


Node leftRotation(Node root){  		// 左旋操作，实际上就是把左边结点拿上来
    Node newRoot = root->right;   	// 先得到左边结点
    root->right = newRoot->left;   	// 将左边结点的左子树丢到原本根结点的右边去
    newRoot->left = root;			// 现在新的根结点左边就是原本的跟结点了

    root->height = max(getHeight(root->right), getHeight(root->left)) + 1;
    newRoot->height = max(getHeight(newRoot->right), getHeight(newRoot->left)) + 1;
    return newRoot;
}


Node rightRotation(Node root){
    Node newRoot = root->left;
    root->left = newRoot->right;
    newRoot->right = root;

    root->height = max(getHeight(root->right), getHeight(root->left)) + 1;
    newRoot->height = max(getHeight(newRoot->right), getHeight(newRoot->left)) + 1;
    return newRoot;
}


Node leftRightRotation(Node root){
    root->left = leftRotation(root->left);
    return rightRotation(root);
}


Node rightLeftRightRotation(Node root){
    root->right = rightRotation(root->right);
    return leftRotation(root);
}


Node insert(Node root, E element){
    if(root == NULL) {    					// 如果结点为NULL，说明找到了插入位置，直接创建新的就完事
        root = createNode(element);
    }else if(root->element > element) {   // 和二叉搜索树一样，判断大小，该走哪边走哪边，直到找到对应插入位置
        root->left = insert(root->left, element);
        if(getHeight(root->left) - getHeight(root->right) > 1) {   	// 插入完成之后，需要计算平衡因子，看看是否失衡
            if(root->left->element > element) 			// 接着需要判断一下是插入了左子树的左边还是右边，如果是左边那边说明是LL，如果是右边那说明是LR
                root = rightRotation(root);   // LL型得到左旋之后的结果，得到新的根结点
            else
                root = leftRightRotation(root);    // LR型得到先左旋再右旋之后的结果，得到新的根结点
        }
    }else if(root->element < element){
        root->right = insert(root->right, element);
        if(getHeight(root->left) - getHeight(root->right) < -1){
            if(root->right->element < element)
                root = leftRotation(root);
            else
                root = rightLeftRightRotation(root);
        }
    }
    // 前面的操作完成之后记得更新一下树高度
    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    return root;  	// 最后返回root到上一级
}

红黑树

  • 动画演示：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
  • 视频推荐：https://www.bilibili.com/video/BV1Xm421x7Lg/
  • 代码实现：https://blog.csdn.net/m0_75215937/article/details/133570625

B树

基本认识

B树 ( Balance Tree )，它是专门为磁盘数据读取设计的一种度为 m 的查找树（多用于数据库）

下面是一棵度为4的B树：

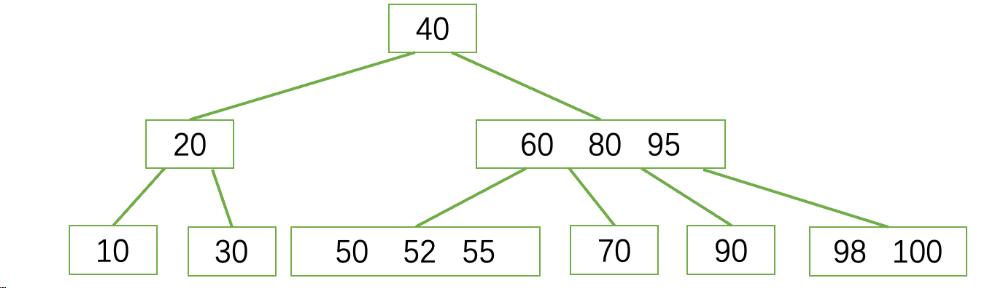
在这里插入图片描述

详细规则

  • 树中每个结点最多含有m个孩子（m >= 2）比如上面就是m为4的4阶B树，最多有4个孩子
  • 除根结点和叶子结点外，其它每个结点至少有⌈m/2⌉个孩子，同理键值数量至少有⌈m/2⌉-1个
  • 若根结点不是叶子结点，则至少有2个孩子
  • 所有叶子结点都出现在同一层
  • 一个结点的包含多种信息（P0，K1，P1，K2，…，Kn，Pn），其中P为指向子树的指针，K为键值（关键字）
  • Ki (i=1…n)为键值，也就是每个结点保存的值，且键值按顺序升序排序K(i-1)< Ki
  • Pi为指向子树的指针，且指针Pi指向的子树中所有结点的键值均小于Ki，但都大于K(i-1)
  • 键值的个数n必须满足： ⌈m/2⌉-1 <= n <= m-1

动画演示

https://www.cs.usfca.edu/~galles/visualization/BTree.html

B+树

基本认识

  • B+树是B树的一种变体，有着比B树更高的查询性能
  • B+树上的叶子结点存储关键字以及相应记录的地址，叶子结点以上各层作为索引使用

B+树的应用

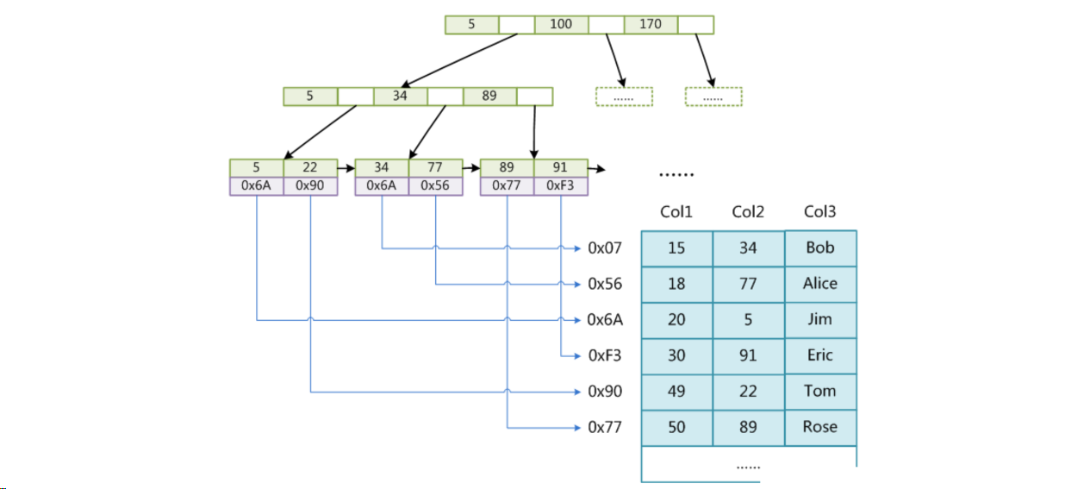
在这里插入图片描述

动画演示

https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

代码演示

https://www.cnblogs.com/yangj-Blog/p/12992124.html

哈夫曼树

基本认识

  • 哈夫曼树（Huffman Tree）又称最优二叉树，是n个带权叶子结点构成的二叉树中，带权路径长度（WPL）最小的二叉树。
  • 哈夫曼编码是一种压缩编码的编码算法，是基于哈夫曼树的一种编码方式。
  • 在计算机数据处理中，哈夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而实现无损压缩数据。

详细内容

https://zhuanlan.zhihu.com/p/415467000

堆

基本认识

  • 堆 (heap) 是计算机科学中一类特殊的数据结构的统称。
  • 堆通常是一个可以被看做一棵树的数组对象
  • 堆总是满足下列性质：
    • 堆中某个节点的值总是不大于或不小于其父节点的值
    • 堆总是一棵完全二叉树

详细内容

https://blog.csdn.net/xiaomucgwlmx/article/details/103522410

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1640443.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

电脑找不到msvcp140.dll如何修复？msvcp140.dll丢失的多种解决方法分享

电脑找不到msvcp140.dll如何修复？msvcp140.dll丢失的多种解决方法分享

在日常电脑操作过程中&#xff0c;用户可能会遇到一个令人困扰的问题&#xff0c;即屏幕上突然弹出一条错误提示&#xff1a;“由于找不到msvcp140.dll&#xff0c;无法继续执行代码”。这一情况往往导致应用程序无法正常启动或运行&#xff0c;给工作和娱乐带来不便。不过&…
阅读更多...
freertos入门---创建FreeRTOS工程

freertos入门---创建FreeRTOS工程

freertos入门—创建FreeRTOS工程 1 STM32CubeMx配置 双击运行STM32CubeMX,在首页选择“ACCESS TO MCU SELECTOR”,如下图所示&#xff1a;   在MCU选型界面&#xff0c;输入自己想要开发的芯片型号&#xff0c;如&#xff1a;STM32F103C8T6: 2 配置时钟 在“System Core”…
阅读更多...
【MATLAB】解决不同版本MATLAB出现中文乱码的问题

【MATLAB】解决不同版本MATLAB出现中文乱码的问题

解决不同版本MATLAB出现中文乱码的问题 方法1&#xff1a;更改保存类型为GBK方法2&#xff1a;记事本打开方法3&#xff1a;Notepad参考 低版本matlab打开高版本Matlab的.m文件时&#xff0c;出现中文乱码问题。比如下图&#xff1a; 出现原因为&#xff1a; 编码格式不统一问…
阅读更多...
【深度学习】第二门课 改善深层神经网络 Week 1 深度学习的实践层面

【深度学习】第二门课 改善深层神经网络 Week 1 深度学习的实践层面

&#x1f680;Write In Front&#x1f680; &#x1f4dd;个人主页&#xff1a;令夏二十三 &#x1f381;欢迎各位→点赞&#x1f44d; 收藏⭐️ 留言&#x1f4dd; &#x1f4e3;系列专栏&#xff1a;深度学习 &#x1f4ac;总结&#xff1a;希望你看完之后&#xff0c;能对…
阅读更多...
力扣---二叉树的锯齿形层序遍历

力扣---二叉树的锯齿形层序遍历

给你二叉树的根节点 root &#xff0c;返回其节点值的 锯齿形层序遍历 。&#xff08;即先从左往右&#xff0c;再从右往左进行下一层遍历&#xff0c;以此类推&#xff0c;层与层之间交替进行&#xff09;。 示例 1&#xff1a; 输入&#xff1a;root [3,9,20,null,null,15,…
阅读更多...
通信光缆主要敷设方式有哪些（续）

通信光缆主要敷设方式有哪些（续）

在《通信光缆主要敷设方式有哪些》一文中&#xff0c;介绍了光缆的直埋、架空和管道敷设方式。此外&#xff0c;根据敷设场景的不同&#xff0c;光缆的常见敷设方式还包括&#xff1a;高铁槽道内敷设、水底敷设、墙壁敷设、引上、室内敷设等。 1 高铁槽道内光缆敷设 光缆顺沿高…
阅读更多...
机器学习每周挑战——二手车车辆信息交易售价数据

机器学习每周挑战——二手车车辆信息交易售价数据

这是数据集的截图 目录 背景描述 数据说明 车型对照&#xff1a; 燃料类型对照&#xff1a; 老规矩&#xff0c;第一步先导入用到的库 第二步&#xff0c;读入数据&#xff1a; 第三步&#xff0c;数据预处理 第四步&#xff1a;对数据的分析 第五步&#xff1a;模型建…
阅读更多...
会声会影电影片头怎么做 会声会影电影质感调色技巧

会声会影电影片头怎么做 会声会影电影质感调色技巧

片头通常通过一系列的图像、音乐和文字等元素来引入电影的主题和氛围。通过视觉和音频的呈现方式&#xff0c;给观众留下深刻的第一印象&#xff0c;为电影的故事铺设基础。这篇文章来学习一下会声会影片头怎么做&#xff0c;会声会影电影质感调色技巧。 一、会声会影电影片头…
阅读更多...
数据库（MySQL）基础：多表查询（一）

数据库（MySQL）基础：多表查询（一）

一、多表关系 概述 项目开发中&#xff0c;在进行数据库表结构设计时&#xff0c;会根据业务需求及业务模块之间的关系&#xff0c;分析并设计表结构&#xff0c;由于业务之间相互关联&#xff0c;所以各个表结构之间也存在着各种联系&#xff0c;基本上分为三种&#xff1a;…
阅读更多...
npm install digital envelope routines::unsupported解决方法

npm install digital envelope routines::unsupported解决方法

目录 一、问题描述二、问题原因三、解决方法 一、问题描述 执行命令 npm install 报错&#xff1a;digital envelope routines::unsupported 二、问题原因 Node.js 17 版本引入了 OpenSSL 3.0&#xff0c;它在算法和密钥大小方面实施了更为严格的限制。这一变化导致 npm 的升…
阅读更多...
badKarma：一款功能强大的网络侦查GUI工具

badKarma：一款功能强大的网络侦查GUI工具

关于badKarma badKarma是一款开源的网络侦查工具&#xff0c;该工具基于Python 3开发&#xff0c;提供了友好的图形化用户接口&#xff0c;可以帮助广大渗透测试人员在网络基础设施安全审计过程中执行网络侦查任务。 badKarma是一个模块化工具&#xff0c;基于python3 GTK套件…
阅读更多...
【研发管理】产品经理知识体系-产品创新流程

【研发管理】产品经理知识体系-产品创新流程

导读&#xff1a;产品创新流程是一个系统性的过程&#xff0c;旨在通过创造和引入新的产品或改进现有产品来满足市场需求、解决用户问题或实现竞争优势。 目录 1、产品创新引论 2、决策基本框架 3、模糊前端 4、产品创新流程模型概论 5、门径管理流程 6、并行工程和集成产…
阅读更多...
基于ssm+jsp+mysql+java的人事管理系统

基于ssm+jsp+mysql+java的人事管理系统

&#x1f49e;文末获取源码联系&#x1f649; &#x1f447;&#x1f3fb; 精选专栏推荐收藏订阅&#x1f447;&#x1f3fb; &#x1f380;《Java精选实战项目-计算机毕业设计题目推荐-期末大作业》&#x1f618;更多实战项目~ https://www.yuque.com/liuyixin-rotwn/ei3euo/d…
阅读更多...
设计模式: 工厂模式

设计模式: 工厂模式

工厂模式&#xff08;Factory Pattern&#xff09;是 Java 中最常用的设计模式之一&#xff0c;这种类型的设计模式属于创建型模式&#xff0c;它提供了一种创建对象的最佳方式。 工厂模式提供了一种创建对象的方式&#xff0c;而无需指定要创建的具体类。 工厂模式属于创建型…
阅读更多...
Linux的Shell脚本详解

Linux的Shell脚本详解

本文目录 一、什么是 Shell 脚本文件 &#xff1f;二、编写Shell脚本1. 基本规则2. shell 变量&#xff08;1&#xff09;创建变量&#xff08;2&#xff09;引用变量&#xff08;3&#xff09;删除变量&#xff08;4&#xff09;从键盘读取变量&#xff08;5&#xff09;特殊变…
阅读更多...
PHP的数组练习实验

PHP的数组练习实验

实 验 目 的 掌握索引和关联数组&#xff0c;以及下标和元素概念&#xff1b; 掌握数组创建、初始化&#xff0c;以及元素添加、删除、修改操作&#xff1b; 掌握foreach作用、语法、执行过程和使用&#xff1b; 能应用数组输出表格和数据。 任务1&#xff1a;使用一维索引数…
阅读更多...
一键实现在VS Code中绘制流程图

一键实现在VS Code中绘制流程图

VS Code是一款常用的IDE&#xff0c;受到许多用户的欢迎和喜爱。而其较为出众的一点&#xff0c;就是较好的可拓展性&#xff0c;即丰富的插件应用&#xff0c;这些应用可以极大地提高生产效率&#xff0c;并优化日常使用。 流程图是一种直观的图示方法&#xff0c;可以用简明…
阅读更多...
富文本编辑器 iOS

富文本编辑器 iOS

https://gitee.com/klkxxy/WGEditor-mobile#wgeditor-mobile 采用iOS系统浏览器做的一款富文本编辑器工具。 原理就是使用WKWebView加载一个本地的一个html文件&#xff0c;从而达到编辑器功能的效果&#xff01; 由于浏览器的一些特性等&#xff0c;富文本编辑器手机端很难做…
阅读更多...
wordpress子比主题美化-为图文列表封面添加动态缩略图特效 多种效果演示

wordpress子比主题美化-为图文列表封面添加动态缩略图特效 多种效果演示

wordpress子比主题-为图文列表文章封面添加动态缩略图特效 给自己子比主题加一个列表文章封面添加动态缩略图 直接复制以下代码&#xff0c;添加到主题自定义CSS代码中即可&#xff0c;下图为效果演示 wordpress子比主题-为图文列表文章封面添加动态缩略图特效 给自己子比主题…
阅读更多...
SpringData JPA - ORM 框架下，打造高效数据访问层

SpringData JPA - ORM 框架下，打造高效数据访问层

目录 一、SpringData JPA 概述 1.1、什么是 JPA 1.2、什么是 ORM 1.3、什么是 Hibernate 1.4、JPA 和 Hibernate 的关系 1.5、JPA 的优势 二、SpringData JPA 实战开发 2.1、依赖 2.2、配置文件 2.3、启动类 2.4、创建实体 2.5、基于 JpaRepository 的 CRUD 三、…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023