hot100 -- 二叉树（上）

🎂二叉树的中序遍历

AC 递归

AC 迭代

🌼二叉树的最大深度

AC DFS递归

AC BFS

🚩翻转二叉树

AC 后序（递归）

AC 中序

🚩对称二叉树

AC 递归

AC 迭代

🌼二叉树的直径

AC 递归

🎂二叉树的层序遍历

AC BFS

🎂二叉树的中序遍历

94. 二叉树的中序遍历 - 力扣（LeetCode）

详细介绍👇

树，二叉树，二叉树遍历，哈夫曼树（详解+刷题）_哈夫曼树前置知识点-CSDN博客

AC 递归

时间 O(n) -- 每个节点只被遍历 1 次；空间 O(n) -- 递归栈，一条链时，最大深度 n

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void inorder(TreeNode* root, vector<int> &ans) {
        if (!root) return;
        inorder(root->left, ans); // 左
        ans.push_back(root->val); // 根
        inorder(root->right, ans); // 右
    }

    vector<int> inorderTraversal(TreeNode* root) { // 不要改给定的接口
        vector<int> res;
        inorder(root, res);
        return res;
    }
};

AC 迭代

栈模拟中序遍历，先遍历到左子树最深处，然后依次遍历栈顶每个节点的右子树

（根也是遍历左子树的一部分）

时间 O(n)，空间 O(n)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;

        // 栈模拟中序遍历
        stack<TreeNode*> stk; // 存的是节点（指针）
        while (root || !stk.empty()) {
            // 遍历到左子树最深处
            while (root) {
                // 先遍历的加入栈底，最深处在栈顶
                stk.push(root); // 节点入栈
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            ans.push_back(root->val);
            // 左子树遍历完，到右子树
            root = root->right;
        }
        return ans;
    }
};

🌼二叉树的最大深度

104. 二叉树的最大深度 - 力扣（LeetCode）

AC DFS递归

时间 O(n)；空间 O(height) -- 二叉树高度，即递归栈的深度

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (!root) return 0;
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    }
};

AC BFS

时间 O(n)，空间 O(n)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    queue<TreeNode*> q;
    int maxDepth(TreeNode* root) {

        if (!root) return 0;
        q.push(root);

        int ans = 0; 
        while (!q.empty()) {
            ans++; // 深度 +1
            int sz = q.size();
            // 拓展当前层所有节点
            while (sz--) {
                TreeNode* node = q.front(); q.pop(); // queue 是 front()
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        return ans;
    }
};

🚩翻转二叉树

226. 翻转二叉树 - 力扣（LeetCode）

AC 后序（递归）

根节点 -> 递归左子树 -> 递归右子树（由于只是“左右翻转”，本题不需处理根节点）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return nullptr; // 递归出口

        TreeNode* right = invertTree(root->right); // 递归右子树
        TreeNode* left = invertTree(root->left); // 递归左子树

        // 回溯--交换当前节点的左右
        root->left = right;
        root->right = left; 

        return root;
    }
};

AC 中序

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return nullptr; // 递归出口

        TreeNode* left = invertTree(root->left); // 递归左子树

        // 回溯 -- 交换左右
        TreeNode* rightNode = root->right;
        root->right = root->left;
        root->left = rightNode;

        // 此时的 root->left 即原来的右子树
        TreeNode* right = invertTree(root->left); // 递归右子树

        return root;
    }
};

🚩对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

AC 递归

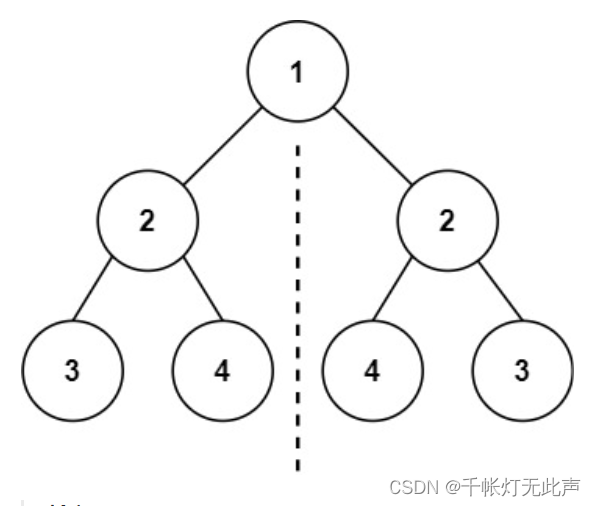
在根节点中间，画一条对称的虚线，左边，右边，看作独立的两棵树，那么问题可以转化为

什么条件下，左右两颗树是对称的呢

1）两个根节点->val 相等（2 == 2）

2）左子树的右子树->val == 右子树的左子树->val（4 == 4）

3）左子树的左子树->val == 右子树的右子树->val（3 == 3）

时空 O(n)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSame(TreeNode* l, TreeNode* r) {
        if (!l && !r) return true; // 2个空
        if (!l || !r) return false; // 1个空

        // 3 个 &&，保证每一对节点都对称，才为 true
        // 但凡出现一次 false，结果就是 false
        bool ans = (l->val == r->val) && isSame(l->right, r->left)
                                      && isSame(l->left, r->right);
        return ans;
    }
    bool isSymmetric(TreeNode* root) {
        if (!root) return true; // 递归出口

        return isSame(root->left, root->right);
    }
};

AC 迭代

用 BFS 进行迭代，队列实现 BFS，详细解析 BFS👇

《啊哈算法第四章之bfs》（17张图解）_图解bfs算法-CSDN博客

时空 O(n)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        queue<TreeNode*> q; // 队列实现 BFS
        TreeNode *u = root, *v = root;
        q.push(u); q.push(v);

        // bfs 一层一层拓展
        while (!q.empty()) {
            // 取两个对称节点
            u = q.front(); q.pop();
            v = q.front(); q.pop();

            // 2个空（对称）
            if (!u && !v) continue; 
            // 1个空 或 值不同（不对称）
            if ( (!u || !v) || (u->val != v->val) ) return false;

            // 此时当前节点 u, v 是对称的，可以继续拓展
            // 按顺序加入两组节点
            q.push(u->left); q.push(v->right);
            q.push(u->right); q.push(v->left);
        }
        return true;
    }
};

🌼二叉树的直径

543. 二叉树的直径 - 力扣（LeetCode）

AC 递归

不要直接对每个节点，调用一次遍历二叉树最大深度的 maxDepth()，这样时间 O(n^2)，而是在 maxDepth() 中，动态更新 ans，当然，maxDepth() 的返回值还是最大深度

时空 O(n)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int ans = 0;

    int maxDepth(TreeNode* root) { // 返回最大深度
        if (!root) return 0; // 递归出口
        
        // 递归
        int L = maxDepth(root->left);
        int R = maxDepth(root->right);

        // 不用 -2，因为L，R都是从子树开始的
        ans = max(ans, L + R); // 边递归边得到结果

        return 1 + max(L, R);
    }

    int diameterOfBinaryTree(TreeNode* root) {
        maxDepth(root);
        return ans;
    }
};

🎂二叉树的层序遍历

102. 二叉树的层序遍历 - 力扣（LeetCode）

AC BFS

关于 vector 的 .back() 👇

std::vector - cppreference.com

std::vector<T,Allocator>::back - cppreference.com

坑 -- 第33，34行

q.push(temp->left) 和 q.push(temp->right) 前，要先判断左 / 右子树存在，否则就会插入空指针 null pointer

时空 O(n)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 队列实现BFS--层序遍历
    vector<vector<int>> levelOrder(TreeNode* root) {

        vector< vector<int> > ans;
        if (!root) return ans;

        queue<TreeNode*> q;
        q.push(root);

        // 一层一层拓展
        while (!q.empty()) {
            // vector<int>() 调用构造函数，创建一个空的 vector 对象
            ans.push_back(vector<int>());
            int size = q.size(); // 当前层节点数

            // 拓展当前层
            for (int i = 0; i < size; ++i) {
                TreeNode* temp = q.front(); q.pop(); // 取队头
                ans.back().push_back(temp->val); // 插入值 val
                if (temp->left) q.push(temp->left);
                if (temp->right) q.push(temp->right);
            }
        }
        return ans;
    }
};