数据下载网址:WWDT Data (dri.edu)![]() https://wrcc.dri.edu/wwdt/data/PRISM/
https://wrcc.dri.edu/wwdt/data/PRISM/
以SPI为例说明,
标准化降水指数(Standardized Precipitation Index, SPI)是由Mckee et al(.1993)分析美国科罗拉多干旱时,发现降水服从偏态分布,基于此提出了标准化降水指数。标准化降水指数通过计算给定时间内降雨量的累计概率,比较客观地表述了多时间尺度下的降水概率,反映降水因素对干旱的影响。Mckee et al.(1993)认为降水量的减少是导致干旱的主要因素,其他气候因子一般变化较小,对干旱产生的影响不大,因此SPI使用降水量作为唯一参数。SPI能较好表达因降水量的大小反映干旱状况,操作简单,所需资料仅为降水量,同时该干旱指数在各个地区和各个时段都具有良好的计算稳定性,是继PDSI之后另一种被广泛应用的干旱指数。
标准化降水指数介绍_标准化降水指数spipython-CSDN博客
下载数据时间跨度为从2002年4月至2014年6月,共147个月。提前准备好如下形式的控制文件:
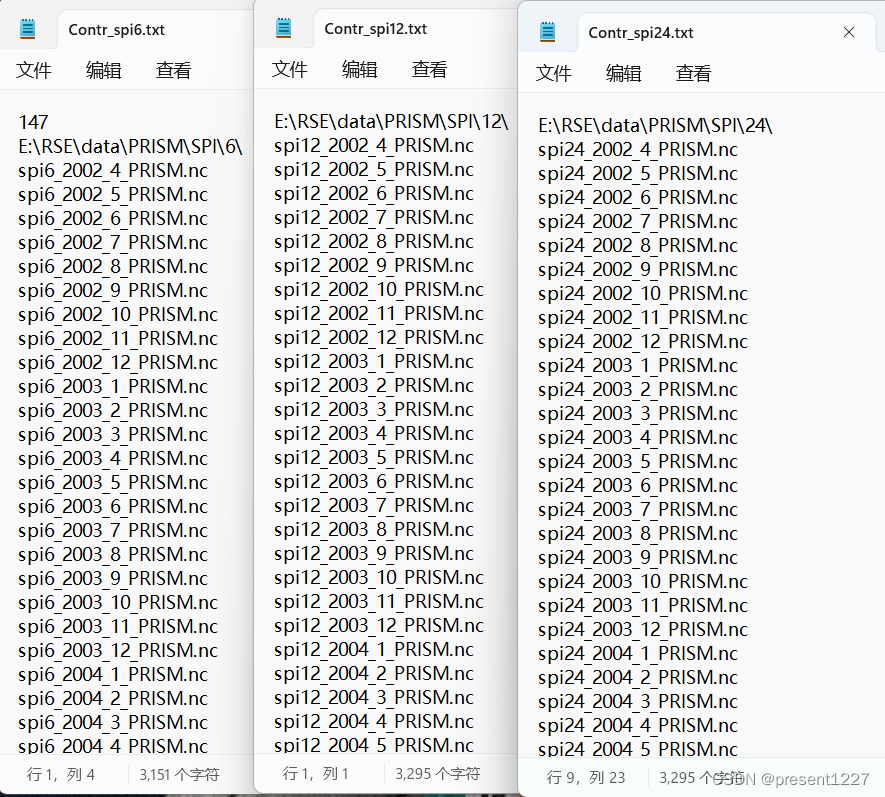
读取SPI数据,并绘制加州中央山谷区域的SPI-6、SPI-12和SPI-24指标时间序列图
clearvars -except Time02_14
info6 = ncinfo('E:\RSE\data\PRISM\SPI\6\spi6_2003_1_PRISM.nc');
fid6=fopen('E:\RSE\data\PRISM\SPI\6\Contr_spi6.txt','r');
fid12=fopen('E:\RSE\data\PRISM\SPI\12\Contr_spi12.txt','r');
fid24=fopen('E:\RSE\data\PRISM\SPI\24\Contr_spi24.txt','r');
load E:\RSE\Result1\Time02_14.mat;
num_file= fscanf(fid6,'%d',1); fig=1;
dir_in6=fscanf(fid6,'%s',1);dir_in12=fscanf(fid12,'%s',1);dir_in24=fscanf(fid24,'%s',1);
for i = 1:num_file
file_name{i,1} = fscanf(fid6,'%s',1);
file_name{i,2} = fscanf(fid12,'%s',1);
file_name{i,3} = fscanf(fid24,'%s',1);
end
for k=1:num_file
data6(:,:,k)=rot90(ncread(strcat(dir_in6,file_name{k,1}),'data'));
data12(:,:,k)=rot90(ncread(strcat(dir_in12,file_name{k,2}),'data'));
data24(:,:,k)=rot90(ncread(strcat(dir_in24,file_name{k,3}),'data'));
end
lon = 360-125:0.041666:360-66.5; lat =50:-0.041666:24.13;[LON,LAT]=meshgrid(lon,lat);
mask = 'E:\RSE\data\Basin\studyregion.vec';rows=3932;
spi6_serie=gmt_grid2regionserie(data6,mask,rows,lon,lat);
spi12_serie=gmt_grid2regionserie(data12,mask,rows,lon,lat);
spi24_serie=gmt_grid2regionserie(data24,mask,rows,lon,lat);
% save SPI6_24.mat spi6_serie spi12_serie spi24_serie
figure(fig)
plot(Time02_14,spi6_serie,'color',[0 0 0],'Linewidth',1.5);hold on;
plot(Time02_14,spi12_serie,'color',[0 1 0],'Linewidth',1.5);
plot(Time02_14,spi24_serie,'--','color',[1 0 1],'Linewidth',1.5);
title('','FontName','Time New Roman','Fontsize',30);
yline(0,'LineStyle','-','Color','red','LabelVerticalAlignment','middle','LabelHorizontalAlignment','center','LineWidth',1.5);
xlim([2002 2015]);
xticks([2002 2004 2006 2008 2010 2012 2014]);
xlabel('Time (year)','Fontname','Time New Roman',"FontSize",10);
ylabel('Index','Fontname','Time New Roman',"FontSize",10);
l1=legend('SPI6','SPI12','SPI24','location','northeast');
set(l1,'box','off',"FontSize",10,'Fontname','Time New Roman');
box on;grid on;fig=fig+1;
值得说明滴是,“Time02_14”为以年为单位的时间变量;函数“gmt_grid2regionserie”如下:
function [plot_region]=gmt_grid2regionserie(grid,dir_msk,rows,lon,lat)
fid = fopen(dir_msk,'r');
num_points = rows;
river_name = fscanf(fid,'%s',1);
xv = zeros(num_points,1);
yv = zeros(num_points,1);
for i=1:num_points
a = fscanf(fid,'%f %f',[1 2]);
xv(i) = a(1);
yv(i) = a(2);
end
fclose(fid);
lon_min=min(xv);lon_max=max(xv);
lat_min=min(yv);lat_max=max(yv);
ii=size(grid,2);jj=size(grid,1);num_file=size(grid,3);
if ii==1405 && jj==621
load E:\RSE\result\lg_msk.mat;%%加州区域的掩膜,区域内为1区域外为0
else
lg_msk = zeros(jj,ii);
for j=1:jj
for i=1:ii
if lon(i)>=lon_min && lon(i)<=lon_max && lat(j)>=lat_min && lat(j)<=lat_max
in =inpolygon(lon(i),lat(j),xv,yv);
if in==1
lg_msk(j,i) = 1;
end
end
end
end
end
grid_weight=zeros(jj,ii);
for j=1:jj
for i=1:ii
grid_weight(j,i)=cos(lat(j)*pi/180);
end
end
grid_weight=grid_weight.*lg_msk;
tmmp=zeros(jj,ii);
% grid(logical(isnan(grid)))=0; % set possible NaNs to zeros
for k=1:num_file
tmmp(:,:)=grid(:,:,k);
grid_weight_new=grid_weight;
tmmppp=tmmp.*grid_weight_new;
tmmppp(logical(isnan(tmmppp)))=0;% in case, there are NaNs
grid_sum=sum(sum(tmmppp));
grid_weight_new(logical(isnan(tmmp)))=0;
weight_sum=sum(sum(grid_weight_new));
plot_region(k,1)=grid_sum/weight_sum;
end
end结果:
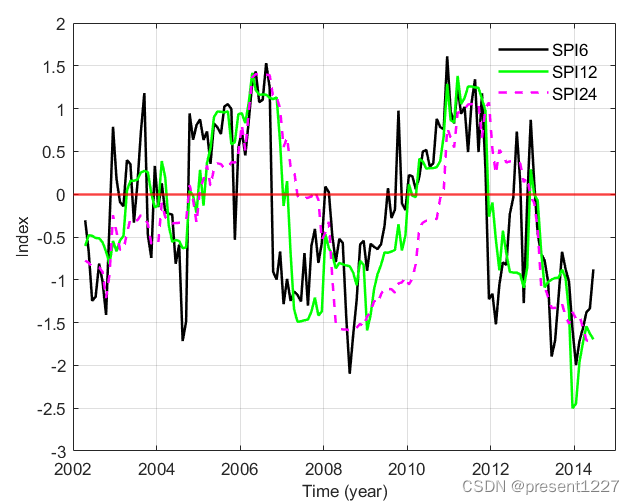
SPEI、PDSI和sc-PDSI类似于上述操作方式,此处省略。如有任何问题,尽情批评指正,欢迎交流!