🦊原文：Merkle DAGs: Structuring Data for the Distributed Web

🦊写在前面：本文属于搬运博客，自己留存学习。

1 Merkle DAG

当我们在计算机上表示图时，必须通过提供节点和边的具体表示来编码我们的数据结构。由于 CID 可以唯一标识一个节点，因此我们可以使用 CID 来表示从一个节点到另一个节点的边。这样我们就创建了一种特殊的 DAG，称为 Merkle DAG 或默克尔有向无环图。

由于 CID 可以唯一标识一个节点，因此我们根据 CID 可以找到相应的节点。假设 A 节点存储了 B 节点的 CID，那么就能从 A 节点找到 B 节点。因此，我们可以使用 CID 来表示节点之间的边。

让我们看看如何构建一个Merkle DAG，以文件目录为例：

pics
├── cats
│   ├── 2018-02-23-tabby.png
│   └── 2019-12-16-black.png
└── fish
    ├── 2017-03-05-freshwater.png
    ├── 2018-04-14-tropical.png
    └── 2020-10-02-blowfish.png

结构如下图所示：

---

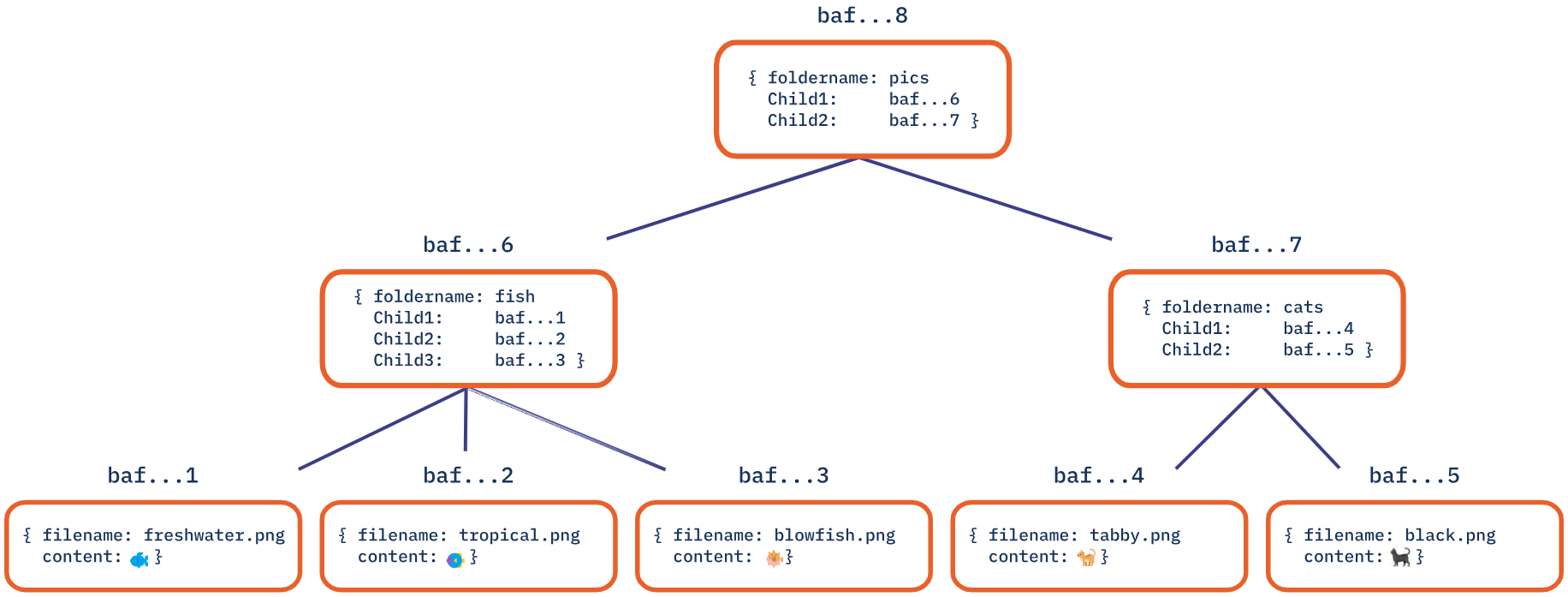
首先对 叶节点 编码，即我们的各个图像文件，并为每个节点赋予一个 CID 。为了简化这个例子，我们将 叶节点 的表示简化为两个属性：文件的名称和文件的内容，从而构成节点的数据。如下图所示：

节点上方的标签是对通过加密哈希算法生成的唯一 CID 的简化表示。请注意，此标签并非节点本身的一部分。

橙色框上面的 baf...1 是该文件的 CID，为了简化表示而省略了中间的内容。

以此类推，目录中每个文件对应的 叶节点 如下：

---

中间节点 的节点结构，即目录中的子目录，必须有所不同。每个节点也将包含一个名称，对应于目录的名称。然而，目录节点的 “内容” 是它所包含的文件和子目录的 “列表”，而不是任何特定文件的内容。

子目录下可能还有子目录，即孙子目录。

我们可以将 “列表” 表示为一组 CID，每个 CID 都链接到图中的另一个节点。子目录的名称和子目录包含的 “列表”，构成了 中间节点 的数据。我们同样可以为该数据生成一个 CID，如下图所示：

在上图中，cats 子目录被表示为一个非常小的 DAG 。具有 CID = baf...7 的节点通过在其数据中嵌入其子节点的 CID = baf...4 和 CID = baf...5，从而形成到子节点的链接。

也就是说，父节点通过存放子节点的 CID，来建立与子节点之间的联系。

---

现在我们已经为图中两种类型的节点规定了表示形式，我们可以继续从下至上构建图：

在 Merkle DAG 中，每个节点的 CID 取决于其所有后代节点。如果任何后代发生变化，那么它们自己的 CID 也会改变。

例如，如果某种程度上修改了虎斑猫的照片，那么图中相应节点的 CID 将会改变。由于子节点的 CID 是父节点数据的一部分，因此在这个例子中，cats 目录本身也会改变，导致它获得一个新的 CID 。进而，pics 目录的节点的 CID 也会改变。这意味着我们总是必须从下而上构建 DAG：父节点不能在确定其子节点的 CID 之前创建。

一般来说，Merkle DAG 中任何节点的变化都会传播到该节点的所有祖先节点。然而，在 DAG 的一个分支上做出的更改不会改变其他分支上节点的 CID；一个节点的 CID 仅在其数据或其后代数据发生变化时才会改变。例如，更改 blowfish.png 不需要 baf...1、baf...2、baf...4、baf...5 或 baf...7 发生变化。

请注意，由节点组成并内嵌其子节点的 CID 的结构必然不包含循环。用于构造 CID 的加密函数以及 Merkle DAG，使得描述图中的一个 “自引用” 路径成为不可能。这是一个重要的安全保证：如果我们遍历 Merkle DAG，我们可以确信自己不会陷入无限循环。

2 Merkle DAG 的属性

既然我们已经了解了如何使用 CID 创建结构化数据，接下来让我们探讨一些我们可以依赖的 Merkle DAG 的属性！

2.1 可验证性

由于我们使用加密哈希算法来创建 CID，因此它们提供了高度的可验证性：使用内容地址检索数据的个人始终可以自己计算 CID，以确保他们得到了自己想要的东西。这提供了：

• 永久性：内容地址背后的数据永远不会改变；
• 对抗恶意操纵：恶意行为者无法诱骗你下载错误的文件，因为你可以识别出它不是你请求的文件；

在 Merkle DAG 中，每个节点的 CID 取决于其每个子节点的 CID 。因此，根节点的 CID 不仅唯一标识了该节点，还唯一标识了以它为根的整个 DAG！结果是，我们可以将 CID 的所有美妙安全性、完整性和永久性保证扩展到我们数据结构本身，而不仅仅是它包含的数据！

2.2 任何节点都可以是根节点

DAG 可以被视为递归数据结构，即每个 DAG 都由更小的 DAG 组成。

如下图所示，CID = baf...8 标识了一个 DAG，但 CID = baf...6 也是如此 —— 它只是标识了一个较小的 DAG，它是被 CID = baf...8 标识的 DAG 的一个子图。相应的节点在适当的上下文中都是根节点。

这是一个极其强大且实用的特性。我们不必检索整个 DAG：我们可以有选择地检索一个子图，它由其顶部节点的 CID 标识，即这个子图的顶部节点将成为其根节点。如果我们想与其他人分享这个子图，我们不必包含大图的上下文，而是只需要发送子图的 CID 。除此之外，如果我们想在另一个 DAG 中嵌入该 DAG，那么我们可以自由地这样做，因为 DAG 的 CID（即其根节点的 CID）取决于根节点的后代节点，而不是其祖先节点。

但那个大 DAG 的 CID 不还是需要改变吗？

最后一点值得特别强调：在 Merkle DAG 中，我们可以将相同的 DAG 无缝地嵌入到多个其他更大的 DAG 中！ 这使得形成一个巨大、互联的 DAG 网络成为可能，它们相互建立在顶部并互相借用部分。

2.3 确保存在根节点

有时，我们的数据并非呈现出一个单一的根节点：这实际上并不是 DAG 的严格要求。例如，考虑以下员工层次结构，其中有两位没有上级的经理和一位有两个经理的员工。如下图所示：

图中没有一个单一的节点作为所有五个节点的根节点，因此使用 baf...1~5 中的任何一个节点来共享或检索整个 DAG 都是不可能的。但我们可以自己创建一个！我们可以通过创建一个额外的节点，该节点将 Asif 和 Ciara 作为自己的子节点，然后以该节点为根节点来创建一个新的 DAG 。

即使 DAG 没有单一的根节点，分享 DAG 的人总是可以创建一个。

另一种选择是，我们可能希望有两个不同的数据结构，即 Asif 和 Ciara 分别作为两个 DAG 的根节点。其中，拥有两个经理的 Padma 节点将包含在这两个 DAG 中。重要的是，这将形成两个独立的 Merkle DAG，因为你不能仅从一个根节点导航到这个数据集中的所有节点

DAG 中的边是单向的，即从 Padma 到 Ciara 没有边。因此，我们不能从 Padma 导航到根节点 Ciara，从而不能从根节点 Asif 导航到 Ciara 或 Aiden。

2.4 分布式特性

Merkle DAG 继承了 CID 的分布式特性。使用内容寻址对 DAG 进行编码有几个有趣的分布式后果：

• 任何拥有 DAG 的人都有能力成为该 DAG 的提供者；
• 可以并行检索节点的所有子节点，从一个或多个不同的提供商那里获取数据；
• 文件服务器不再是集中的数据中心，这使得我们的数据覆盖范围更广；
• 每个节点都有自己的 CID，它所表示的 DAG 可独立于其嵌入的较大 DAG 进行共享和检索。

案例研究：分发大型数据集

以一个大型、流行、科学数据集的分布为例。在今天基于位置寻址的互联网上：

• 分享文件的研究人员负责维护文件服务器及其相关成本；
• 同一个服务器可能被用来响应全世界的请求；
• 数据本身可能以单一文件归档的形式集中分布；
• 很难找到相同数据的替代提供商；
• 数据可能很大块，还必须从一个提供商那里串行下载；
• 其他人很难分享基于原始数据构建的数据集。

Merkle DAG 帮助我们缓解了所有这些问题。通过将数据集作为内容寻址的 DAG 进行分发：

• 任何想要的人都可以帮助分发文件；
• 全世界的节点都可以参与提供数据；
• DAG 的每个节点都有自己的 CID，可以独立分布；
• 很容易找到相同数据的替代提供商；
• 构成 DAG 的节点很小，还可以从许多不同的提供商那里并行下载；
• 一个包含原始数据的大型数据集只需将原始数据集作为更大 DAG 的子节点。

所有这些都有助于促进对重要数据的可扩展和冗余访问。

3 Merkle DAG 去重

3.1 小规模数据

作为一个小规模数据重复的例子，考虑随着时间的推移跟踪目录中文件的变化情况，这通常被称为版本控制。

我们对这个目录所做的变化之一是删除 fish 目录，用一个名为 dogs 的目录替换它。这些变化导致了一个新的 DAG，代表更新后的目录。由于 cats 目录及其文件的所有节点在两个 DAG 中都相同，因此我们可以重复使用它们，如下图所示：

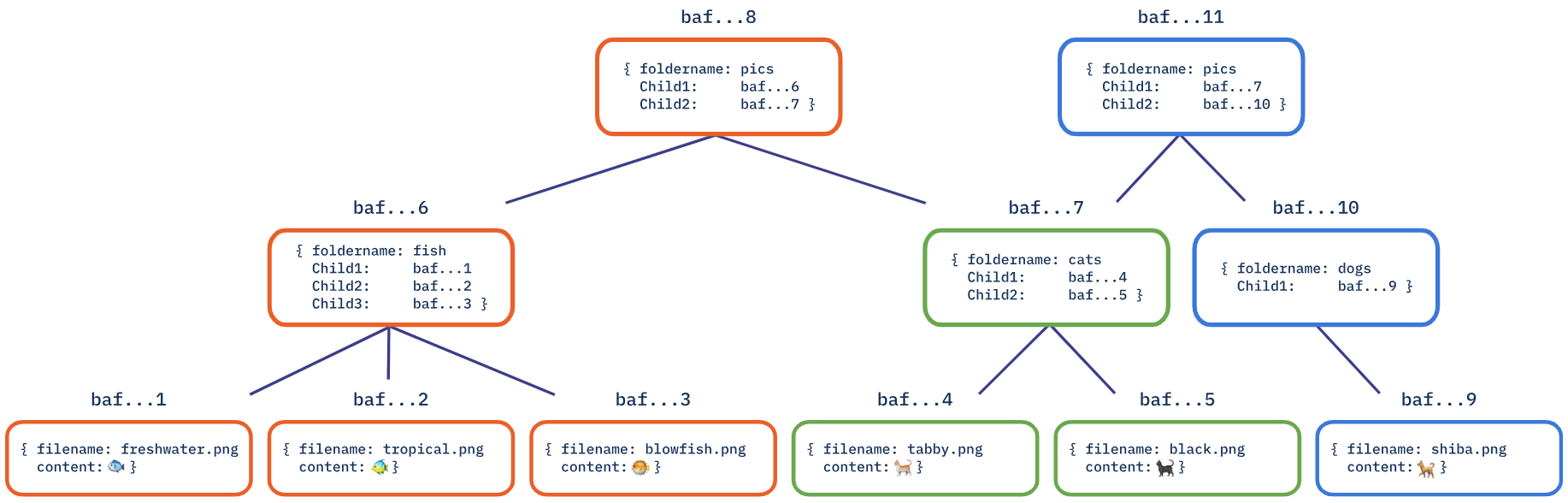
其中，橙色节点代表仅在原始 DAG 中使用的节点，绿色节点代表两个 DAG 共有的节点，蓝色节点代表更新后所需的额外节点。

虽然我们存储了 pics 目录的两个版本，但是并不会占用一个版本两倍的空间！Git 作为一个常见的版本控制系统，正是以类似的方式使用 Merkle DAG 来跟踪软件项目中源代码的变化！

3.2 大规模数据

当我们将这个概念扩展到更大的规模时，去重的影响变得更加显著。例如，考虑浏览网页的场景！当一个人使用浏览器访问网页时，浏览器必须首先下载与页面相关的任何资源，包括图片、文本和样式标记。你可能注意到了，很多网页实际上看起来相当相似，都使用了稍有不同的通用主题。通常，这里有很多冗余 —— 主题大部分相同，只有描述它们的数据显示了一些小的调整。

在基于位置寻址的网络中，尽管这些主题共享大量相同的数据，但通常还是会完全重新下载，因为没有简单的方法来识别这种冗余。相比之下，如果使用 Merkle DAG 来分发主题，它们将共享一个可识别的共同核心，这个核心从一个主题到另一个主题保持不变，因此浏览器可以智能地避免多次下载这个组件。每当用户访问一个使用主题变体的全新网站时，浏览器只需下载 DAG 对应的节点部分，这些部分是不同的，而其他部分已经提前下载过了！对于在互联网上极为广泛使用的资源，这可能使得大量的无谓下载减少！

基于内容寻址使得我们能够形成某种全球分布式文件系统。使用 Merkle DAG，你可以 “存储” 一个大数据集，而实际上并不需要真正存储它：只要你有互联网连接，你就可以在任何给定时间检索到你需要的数据。实际上，没有人需要存储整个数据集！CID 允许我们在计算机之间无缝链接和构建数据集合，帮助每个人都更有效地使用存储空间。尽管也应该指出，有时我们也希望复制数据以提供冗余。

我们的 DAG 粒度也不受限制：我们可以将文件分成多个块并从中创建一个 DAG，而不是使用与整个文件相对应的大型节点！当我们这样做时，我们通常可以找到方法来删除类似文件的重复内容！

4 Merkle DAG 作为构建块

Merkle DAG 为我们提供了一种灵活的方式来在分布式网络上建模和共享数据。这是一个基础能力，事实上，Merkle DAG 是许多不同项目的基本构建块：像 Git 这样的版本控制系统、像以太坊这样的区块链、像 IPFS 这样的去中心化网络协议以及像 Filecoin 这样的分布式存储网络，都使用 Merkle DAG 来存储和传输数据！

这种广泛的应用说明了 Merkle DAG 可能具有作为不同项目之间通信的共同基础的潜力。为了实现这一点，一个名为 IPLD 的项目正在开发一个基于 Merkle DAG 的数据格式及其正式描述的生态系统，以支持广泛的数据交换。就像 CID 为内容寻址数据提供了一种共同的引用语言一样，IPLD 定义了作为结构化和传输内容寻址数据结构的正式模式的通用格式。

能够解析 IPLD 数据和 CID 的系统可以引用其他系统中的内容。例如，我们可以有一个 Filecoin 交易引用 IPFS 中的数据块，或者一个基于区块链的智能合约引用特定的 Git 提交！CID 使我们能够给每个数据片段赋予一个唯一的全球地址，Merkle DAG 和 IPLD 给了我们一种遍历和理解数据结构的方式。它们共同构成了一个全球互连且相互可理解的数据生态系统的基础。