BST与其验证
- 前言
- 我的思路
- 思路一 中序遍历+判断数组无重复递增
- 思路二 递归+边界最大值最小值的传递
- 我的代码
- 测试用例1
- 测试用例2
前言
BST是二叉树一个经典应用,我们常常将其用于数据的查找以及构建平衡二叉树等。今天我所做的题目是验证一颗二叉树是否为二叉搜索树,应该还算是基础题吧。
我的思路
其实最开始这个题目我的思路并不清晰,基本上只能想到去用递归,但是如何去构建递归的子问题,我想不太到,哈哈哈还是算法小白呢,想不到很正常(偷偷安慰自己…)。思路学习链接:
小浩算法-BST验证
力扣–验证二叉搜索树【98】
思路一 中序遍历+判断数组无重复递增
这个思路我觉得很巧妙,因为它利用了一个特性:二叉搜索树的中序遍历得到的一定是一个完全递增的序列(我们考虑的是二叉树里面无重复值),随后我们只需要判断一下遍历的结果是否严格递增就好了。总结一下:
- 先中序遍历BST把结果存储在一个vector里面。
- 判断该vector是否严格递增。
//验证是否为二叉搜索树
void isBST(node* root) {
//先创建一个数组
vector<char> midOrderArr;
midOrder(root, midOrderArr);
//输出看一下我的数组里面存的是不是中序遍历的值
for (int i = 0; i < midOrderArr.size(); i++) {
cout << midOrderArr[i] << ' ';
}
cout << endl;
for (int i = 0; i < midOrderArr.size()-1; i++) {
if (midOrderArr[i] >= midOrderArr[i + 1]) {
cout << "该二叉树 不是一颗二叉搜索树!" << endl;
return;
}
}
cout << "该二叉树 是一颗二叉搜索树!" << endl;
}
//二叉树的中序遍历
void midOrder(node* root,vector<char>& Arr) {
if (root == nullptr) {
return;
}
midOrder(root->left, Arr);
Arr.push_back(root->info);
midOrder(root->right, Arr);
}
思路二 递归+边界最大值最小值的传递
这个题目有一个很有意思的陷阱,那就是我们不光要求 一个结点的左孩子比它小,右孩子比它大。我们要求的是,这个结点的左子树上的所有结点都比它小,右子树上的所有结点都比他大。
因此在递归的时候,我们需要
一个上界和下界。
首先需要考虑初始化的问题,这里我们用到climits库里面的LONG_MAX和LONG_MIN.代表long long 类型的最大值和最小值。
递归左子树,上界是根节点的值,下界就选上一层的min ;递归右子树,下界是根节点的值,上界就选上一层的max。perfect!完美!
bool isBST_Recursion(node* root,long long min,long long max) {
if (root == nullptr) {
return true;
}
if (root->info <= min || root->info >=max) {
//cout << "该二叉树不是一个二叉搜索树";
return false;
}
return isBST_Recursion(root->left, min, root->info) && isBST_Recursion(root->right, root->info, max);
}
我的代码
测试用例1
1248##9##5##36##7##
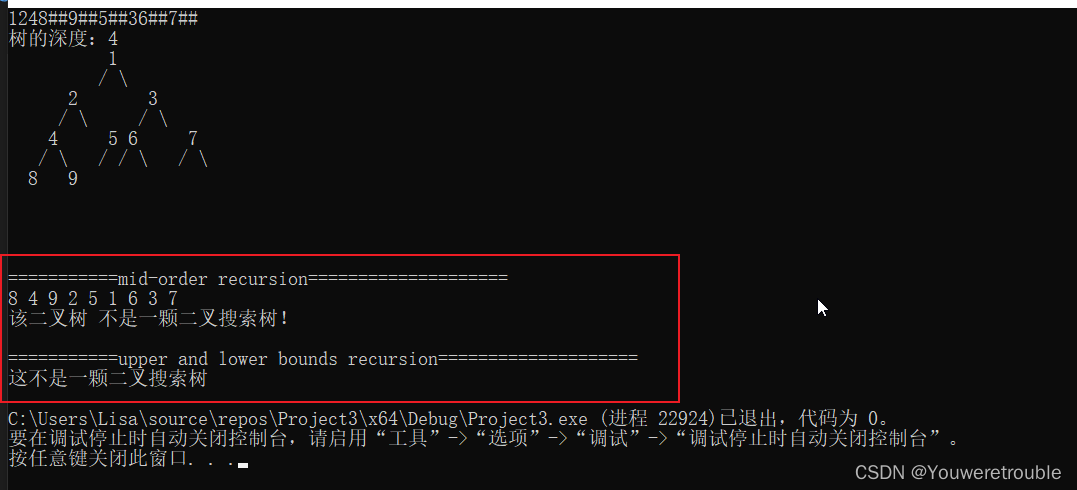
测试用例2
421##3##65##7##
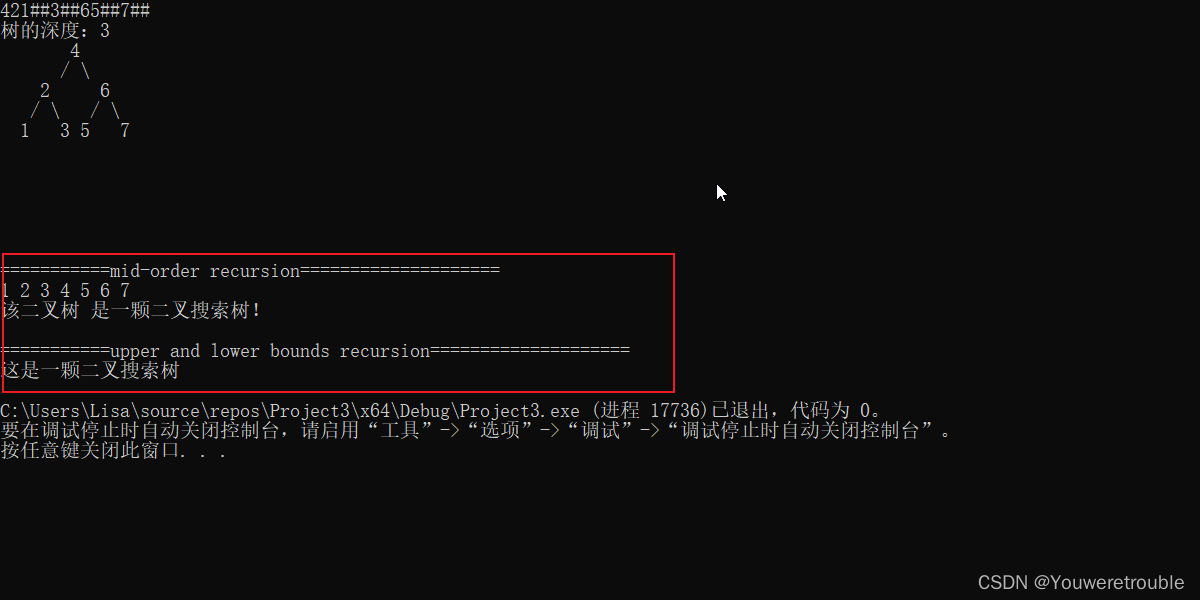
#include <iostream>
#include<algorithm>
#include<cmath>
#include <queue>
#include<climits>
using namespace std;
struct node {
char info;
node* left;
node* right;
node(char data) :info(data), left(nullptr), right(nullptr) {
};
node() :info(NULL), left(nullptr), right(nullptr) {
};
};
class binaryTree {
private:
node* root;
public:
binaryTree() {
root = new node(NULL);
}
//得到树的根结点
node* getRoot() {
return root;
}
//以递归的方式构建一棵树
void createTree(node*& t) {
char str;
cin >> str;
if (str == '#') {
t = NULL;
}
else {
t = new node;//为t开辟空间
t->info = str;
createTree(t->left);
createTree(t->right);
}
}
//树的深度
int depth(node* root) {
if (root == nullptr) {
return 0;
}
int left = depth(root->left);
int right = depth(root->right);
return max(left, right) + 1;
}
//打印一棵树满二叉树,只能打印满二叉树,节点数目最好不要超过10
void print(node*& root) {
//存放打印的二叉树
char str[10][100] = {};
queue<node*> q;
int h = depth(root);
q.push(root);
int index = 0;
while (!q.empty()) {
int size = q.size();
//存放每一层的节点
vector<char> list;
for (int i = 0; i < size; i++) {
node* temp = q.front();
q.pop();
list.push_back(temp->info);
//cout << temp->info;
if (temp->left != nullptr) {
q.push(temp->left);
}
if (temp->right != nullptr) {
q.push(temp->right);
}
}
bool flag = true;
int j = 0;
//打印前面部分空白
while (j <= 2 * h - 1 - index) {
str[index][j] = ' ';
j++;
}
//保持第一行居中
if (index == 0) {
for (int m = 0; m < h - 2; m++) {
str[index][j++] = ' ';
}
}
for (int k = 0; k < list.size(); k++) {
//如果是一层最后一个节点
if (k == list.size() - 1) {
str[index][j++] = list[k];
}
else {
//相邻左右子节点
if (k % 2 == 0) {
str[index][j++] = list[k];
for (int l = 0; l < 3 + 2 * (h - index / 2 - 1); l++) {
str[index][j++] = ' ';
}
}
else {
str[index][j++] = list[k];
str[index][j++] = ' ';
}
}
}
index += 2;
//cout << endl;
}
for (int i = 0; i < 10; i++) {
if (i % 2 == 1) {
for (int j = 0; j < 100; j++) {
str[i][j] = ' ';
}
}
}
for (int i = 0; i < 10; i++) {
if (i % 2 == 0) {
for (int j = 0; j < 100; j++) {
if (str[i][j] - '0' >= 0 && str[i][j] - '0' <= 9 && i < 2 * h - 2) {
str[i + 1][j - 1] = '/';
str[i + 1][j + 1] = '\\';
}
}
}
}
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 100; j++) {
cout << str[i][j];
}
cout << endl;
}
}
void DeepFirstSearch(node* root) {
if (root == NULL) {
return;
}
else {
cout << root->info << ' ';
DeepFirstSearch(root->left);
DeepFirstSearch(root->right);
}
}
void BreadthFirstSearch(node* root) {
queue<node> myTree;
if (root != nullptr) {
myTree.push(*root);
}
while (!myTree.empty()) {
cout << myTree.front().info << ' ';
if (myTree.front().left != nullptr) {
myTree.push(*(myTree.front().left));
}
if (myTree.front().right != nullptr) {
myTree.push(*(myTree.front().right));
}
myTree.pop();
}
}
//用于BFS递归的主函数
void BFS_Recursion(node* root, int level, vector<vector<char>>& res) {
if (root == nullptr) {
return;
}
if (res.size() < level) {
res.push_back(vector<char>());
}
res[level - 1].push_back(root->info);
BFS_Recursion(root->left, level + 1, res);
BFS_Recursion(root->right, level + 1, res);
}
void BreadthFirstSearch_recursion(node* root) {
vector<vector<char>> res;
BFS_Recursion(root, 1, res);
for (int i = 0; i < res.size(); i++) {
for (int j = 0; j < res[i].size(); j++) {
cout << res[i][j] << " ";
}
}
}
//验证是否为二叉搜索树
void isBST(node* root) {
//先创建一个数组
vector<char> midOrderArr;
midOrder(root, midOrderArr);
//输出看一下我的数组里面存的是不是中序遍历的值
for (int i = 0; i < midOrderArr.size(); i++) {
cout << midOrderArr[i] << ' ';
}
cout << endl;
for (int i = 0; i < midOrderArr.size()-1; i++) {
if (midOrderArr[i] >= midOrderArr[i + 1]) {
cout << "该二叉树 不是一颗二叉搜索树!" << endl;
return;
}
}
cout << "该二叉树 是一颗二叉搜索树!" << endl;
}
//二叉树的中序遍历
void midOrder(node* root,vector<char>& Arr) {
if (root == nullptr) {
return;
}
midOrder(root->left, Arr);
Arr.push_back(root->info);
midOrder(root->right, Arr);
}
bool isBST_Recursion(node* root,long long min,long long max) {
if (root == nullptr) {
return true;
}
if (root->info <= min || root->info >=max) {
//cout << "该二叉树不是一个二叉搜索树";
return false;
}
return isBST_Recursion(root->left, min, root->info) && isBST_Recursion(root->right, root->info, max);
}
};
int main() {
binaryTree T;
node* root = T.getRoot();
T.createTree(root);
cout << "树的深度:" << T.depth(root) << endl;
T.print(root);
cout << "\n===========mid-order recursion===================="<<endl;
T.isBST(root);
cout << "\n===========upper and lower bounds recursion====================" << endl;
if (T.isBST_Recursion(root, LONG_MIN, LONG_MAX)) {
cout << "这是一颗二叉搜索树" << endl;
}
else {
cout << "这不是一颗二叉搜索树" << endl;
}
/*cout << "\n===========DFS recursion====================" << endl;
T.DeepFirstSearch(root);
cout << "\n===========BFS QUEUE====================" << endl;
T.BreadthFirstSearch(root);
cout << "\n===========BFS recursion====================" << endl;
T.BreadthFirstSearch_recursion(root);*/
return 0;
}