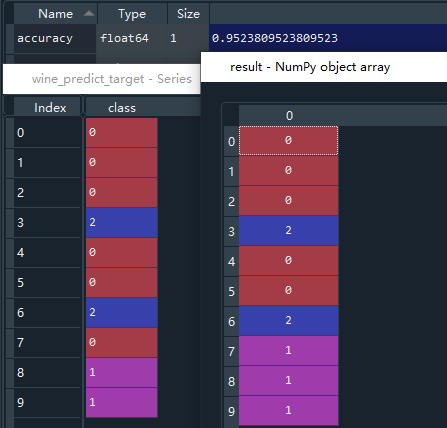
输出结果展示:
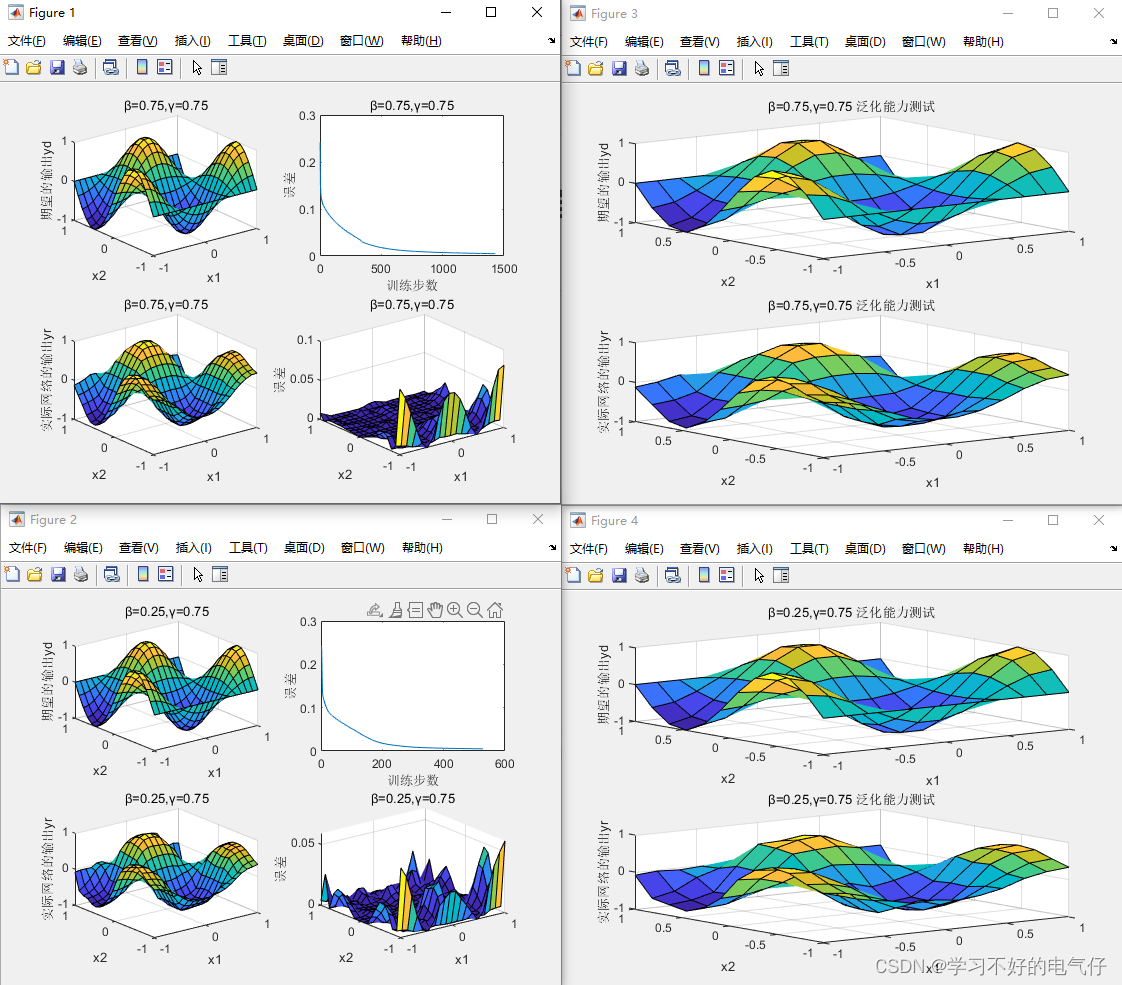
完整代码:
clear;close all;
gamma=0.75;%设定惯性因子
eps1=0.005;%设定停止训练的条件参数
m1=8;%设定隶属函数个数
m2=8;
a=-1;b=1;
w0=a+(b-a)*rand(1,m1*m2);%初始化权值阵
for i=1:2
switch i
case 1,beta=0.75;%设定学习率
otherwise,beta=0.25;
end
c=[2/7*(0:m1-1)-1;2/7*(0:m2-1)-1];%初始化Cij
sigma=0.1213*ones(2,m1);%初始化σij
w=w0;
mu=zeros(2,m1);%初始化隶属度层
alpha=zeros(1,m1*m2);%初始化规则层
alpha_=zeros(1,m1*m2);%初始化归一化层
delta2=zeros(2,m1);%初始化δ2
dw=zeros(1,m1*m2);%初始化权值变化量
dc=zeros(2,m1);%初始化c变化量
dsigma=zeros(2,m1);%初始化σij变化量
%----------------训练过程----------------%
err=1;%初始化误差
er=[];
counter=0;%统计训练步数
while(err>=eps1)
Par_E_w=zeros(1,m1*m2);%误差对权值阵的偏导数
Par_E_c=zeros(2,m1);%误差对c的偏导数
Par_E_sigma=zeros(2,m1);%误差对σ的偏导数
E=0;
for x1=-1:2/19:1
for x2=-1:2/19:1
yd=sin(pi*x1)*cos(pi*x2);%期望输出,导师信号
%正向传播
mu(1,:)=exp(-(x1-c(1,:)).^2./sigma(1,:).^2);%计算隶属度层
mu(2,:)=exp(-(x2-c(2,:)).^2./sigma(2,:).^2);
s=zeros(2,m1,m1*m2);%初始化Sij
for m=1:m1
for n=1:m2
alpha((m-1)*m2+n)=min(mu(1,m),mu(2,n));%计算规则层(取小运算)
if mu(1,m)<=mu(2,n)
s(1,m,(m-1)*m2+n)=1;
end
if mu(1,m)>=mu(2,n)
s(2,n,(m-1)*m2+n)=1;
end
end
end
alpha_=alpha/sum(alpha);%计算归一化层
y=alpha_*w.';%计算网络输出
E=E+1/2*(yd-y)^2;%计算误差
%反向传播
delta5=yd-y;
delta4=delta5*w;
for k=1:m1*m2
delta3(k)=delta4(k)*(sum(alpha)-alpha(k))./sum(alpha)^2;
end
for m=1:2
for n=1:m1
delta2(m,n)=0;
for l=1:m1*m2
delta2(m,n)=delta2(m,n)+delta3(l)*s(m,n,l)*mu(m,n);
end
end
end
Par_E_w=Par_E_w-delta5*alpha_;%计算偏导数
Par_E_c(1,:)=Par_E_c(1,:)-2*delta2(1,:).*(x1-c(1,:))./sigma(1,:).^2;
Par_E_c(2,:)=Par_E_c(2,:)-2*delta2(2,:).*(x2-c(2,:))./sigma(2,:).^2;
Par_E_sigma(1,:)=Par_E_sigma(1,:)-2*delta2(1,:).*(x1-c(1,:)).^2./sigma(1,:).^3;
Par_E_sigma(2,:)=Par_E_sigma(2,:)-2*delta2(2,:).*(x2-c(2,:)).^2./sigma(2,:).^3;
end
end
num=20*20;
Par_E_w=Par_E_w/num;
Par_E_c=Par_E_c/num;
Par_E_sigma=Par_E_sigma/num;
dw=-beta*Par_E_w+gamma*dw;
dc=-beta*Par_E_c+gamma*dc;
dsigma=-beta*Par_E_sigma+gamma*dsigma;
w=w+dw;
c=c+dc;
sigma=sigma+dsigma;
counter=counter+1;
er(counter)=E/num;
err=E/num;
% if counter>1000
% break;
% end
end
%----------------测试过程----------------%
xx1=-1:2/19:1;
xx2=-1:2/19:1;
yd1=zeros(20,20);
for m=1:20
for n=1:20
yd1(m,n)=sin(pi*xx1(m))*cos(pi*xx2(n));%期望输出
mu(1,:)=exp(-(xx1(m)-c(1,:)).^2./sigma(1,:).^2);%计算隶属度层
mu(2,:)=exp(-(xx2(n)-c(2,:)).^2./sigma(2,:).^2);
for k=1:m1 %计算规则层
for l=1:m2
alpha((k-1)*m2+l)=min(mu(1,k),mu(2,l));
end
end
alpha_=alpha/sum(alpha);%计算归一化层
yr(m,n)=alpha_*w.'; %计算网络输出
end
end
errorf1=1/2*(yd1-yr).^2;%计算误差
xxx1=-1:2/11:1;
xxx2=-1:2/11:1;
yd2=zeros(12,12);
for m=1:12
for n=1:12
yd2(m,n)=sin(pi*xxx1(m))*cos(pi*xxx2(n));%期望输出
mu(1,:)=exp(-(xxx1(m)-c(1,:)).^2./sigma(1,:).^2);%计算隶属度层
mu(2,:)=exp(-(xxx2(n)-c(2,:)).^2./sigma(2,:).^2);
for k=1:m1 %计算规则层
for l=1:m2
alpha((k-1)*m2+l)=min(mu(1,k),mu(2,l));
end
end
alpha_=alpha/sum(alpha);%计算归一化层
yr2(m,n)=alpha_*w.'; %计算网络输出
end
end
errorf2=1/2*(yd1-yr).^2;%计算误差
%----------------绘图----------------%
figure(i);
sn=sprintf('β=%4.2f,γ=%4.2f',beta,gamma);
X=ones(size(xx2.'))*xx1;
Y=xx2.'*ones(size(xx1));
subplot(2,2,1);
surf(X,Y,yd1);
xlabel('x1');
ylabel('x2');
zlabel('期望的输出yd');
title(sn);
subplot(2,2,3);
surf(X,Y,yr);
xlabel('x1');
ylabel('x2');
zlabel('实际网络的输出yr');
title(sn);
subplot(2,2,2);
plot(er);
xlabel('训练步数');
ylabel('误差');
title(sn);
subplot(2,2,4);
surf(X,Y,errorf1);
xlabel('x1');
ylabel('x2');
zlabel('误差');
title(sn);
figure(i+2);
sn=sprintf('β=%4.2f,γ=%4.2f 泛化能力测试',beta,gamma);
X=ones(size(xxx2.'))*xxx1;
Y=xxx2.'*ones(size(xxx1));
subplot(2,1,1);
surf(X,Y,yd2);
xlabel('x1');
ylabel('x2');
zlabel('期望的输出yd');
title(sn);
subplot(2,1,2);
surf(X,Y,yr2);
xlabel('x1');
ylabel('x2');
zlabel('实际网络的输出yr');
title(sn);
beta
counter
end


![[ 环境搭建篇 ] 安装python环境并配置环境变量(附python3.10.3安装包)](https://img-blog.csdnimg.cn/7a46c2927e7d4a8b801bcf891d284c94.png)








![[Zombodb那些事]Zombodb执行引擎](https://img-blog.csdnimg.cn/img_convert/f2ba3a76832b7191c61e6011848dd814.png)