题目说的其实是有点乱的,所以我们可能抓不住重点,甚至都不太清楚规则,比如 eg. 

quality=[3,1,10,10,1] wage=[4,8,200,200,7]  这里是选下标0,1,4 ->单价为8

        但是想清楚其实就很easy.  就是 贪心(sort) + 优先队列

        梳理下我们发现其实要让每个人得到最低期望,就要按照当前最贵的人来安排,这里的最贵指的就是cost[i] = wage[i] *1.0 / quality[i] 最高.cost[i]表示单价

        另外看数据量是1e4,最多使用nlogn,而且因为不要求连续 ,所以我们可以使用sort进行优化,(btw. 如果要求连续,就可以使用单调队列,而且单调队列是O(1),优先队列是O(logn),可以处理1e5),优化的思路也和 lc 2398类似(详见我的题解), 简单来说就是总花费就是 sum(quality)*max(单价), 所以按照quaility升序排序,这样越往后其实sum这一项就越大,因此我们要让max变小,也就是不选max对应的那一项,选第二大...

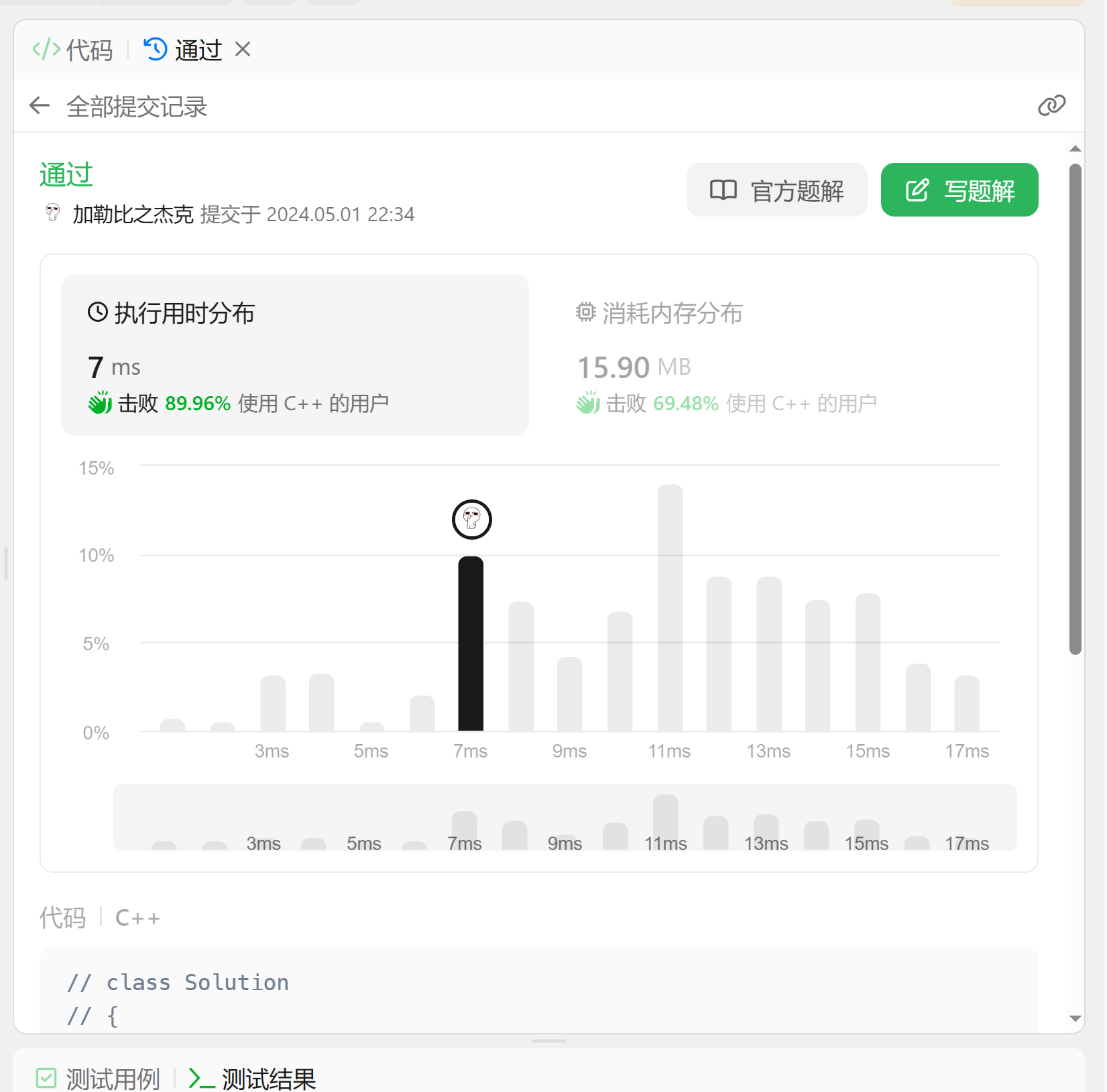
        参考代码如下: 时间复杂度O(nlogn) 空间复杂度O(n) 

class Solution {
public:
    double mincostToHireWorkers(vector<int>& quality, vector<int>& wage, int k) {
        int len=quality.size();
        vector<double> cost;
        vector<int> index;
        for(int i=0;i<len;i++){
            cost.push_back(wage[i]*1.0/quality[i]);
            index.push_back(i);
        }
        sort(index.begin(),index.end(),[&](const int a,const int b){
            if(quality[a]!=quality[b]) return quality[a]<quality[b];
            else return cost[a]<cost[b];
        });
        priority_queue<pair<double,int>> pq;//优先队列使用 pair 不需要 less<pair<...>>
        int sum=0,left=0;
        double ans=INT_MAX;
        for(int i=0;i<len;i++){
            int idx=index[i];
            sum+=quality[idx];
            pq.push({cost[idx],idx});
            if(i-left+1>=k){
                ans=min(ans,sum*pq.top().first);
                sum-=quality[pq.top().second];
                pq.pop();
                left++;
            }
        }
        return ans;
    }
};
// pq 优先队列 主要用 仿函数 或者 重载<
// 仿函数(functor)，其实现就是类中实现一个operator()，这个类就有了类似函数的行为。
// 仿函数不是函数 而是类
// 仿函数主要用在模板类里面
// 一般这种不连续的题目不需要使用 deque 双端队列,