1.含义规则特性
二叉搜索树也叫排序二叉树、有序二叉树,为什么这么叫呢?名字由来是什么?主要是它的规则
图一

规则一,左子树的所有节点的值均小于它的根节点的值
规则二,右子树的所有节点的值均大于它的根节点的值,所以它就是有序的,我们可以更快的找到目标值
规则三,任意左节点和右节点的值均是二叉搜索树
需要注意的是:二叉搜索树极端情况下会退化成链表,这样的情况搜索的时间复杂度会变为O(n),尤其是树的值是有序存储时会产生极端情况,出现这种情况我们就需要调整它的平衡,那么调整它的平衡的办法有AVL树、2-3树、红黑树,这些平衡的办法都是通过在发生不平衡时进行旋转来达到平衡。
2. 实现
2.1 我们先来定义各树枝的节点,定义个内部类Node,一个是节点值val,父类结点parent,左结点left,右结点right。
public class Node {
// 当前值
private Integer val;
// 父节点
private Node parent;
// 左节点
private Node left;
// 右节点
private Node right;
public Node(int val, Node parent, Node left, Node right) {
this.val = val;
this.left = left;
this.right = right;
this.parent = parent;
}
}2.2 插入节点
主要先插入根节点,这就是地基,后进入的都要和各个根节点、左右节点比对,小于它的根节点,放入左边即可,大于放入右边即可,我们还需要循环找位置,直到search寻找到空则证明可以放入它的左右节点,再通过判断左或右加入到此节点中,还是蛮简单的,如果你觉得绕,可以断点调试,看几遍就OK了
public Node insert(int e) {
// 没有根元素添加根元素
if (root == null) {
root = new Node(e, null, null, null);
return root;
}
Node parent = root;
Node search = root;
// 循环取左右元素,看当前要存储的元素要挂到哪个节点下
while (search != null) {
// 将每一次判断完的左右元素赋值给parent,这样退出循环时就可以在他的左右节点挂值,相当于上一个节点
parent = search;
// 判断值大小即可知道左节点右节点,取出有值则循环,没值则退出循环
if (search.val > e) {
search = search.left;
} else {
search = search.right;
}
}
Node newNode = new Node(e, parent, null, null);
if (parent.val > newNode.val) {
parent.left = newNode;
} else {
parent.right = newNode;
}
return parent;
}
/*
* 32
* 7 64
* 6 14 63 89
* 18 72
* 我们先来看一下,它的规律是,左边的树不论是那个节点都比自己的根节点小,右节点都比根节点大
* 按总的一个根节点(例:32)来说,它的所有左节点都比根节点小,所有的右节点都比根节点大
* 这样的一个规律,我们就可以统一判断当前值是否小于或大于循环比对的值,小于放左边,大于放右边即可
* 如果有值则继续循环找空,直到没有值进行各个父节点给左右节点存储当前值即可
*
* 1.假如存储32因为是第一个值直接存储到节点中
* 2.假如存储7需要比对32的值发现7比32小放左边,然后创建新的节点,当前节点为7,父节点为32,存储在32的左边
* 3.假如存储64需要循环比对,先比对32发现比32大放右边,32的右边没有值为空,此时创建新的节点,当前节点为64,父节点为32,存储32的右边
* 4.假如存储6需要循环比对,比对32的值发现6比32小放左边,左边此时有7,所以赋值临时变量,再次进入循环7比对6,发现7比6大,放左边
* 此时7的左边是空,这时退出循环,创建新节点(当前节点为6,父节点为7),存储在7的左边
* 5.此时存储14,需要循环比对,比对32的值发现14比32小,找左边,左边发现有值为7,再次赋值临时变量,进入循环7比14,7小于
* 14,找到7的右边发现为空,退出循环创建新节点(当前节点为14,父节点为7),存储7的左边
* */2.3 根据值搜索节点
主要是遍历查询是否有和参数相等的值,如果当前的值大于节点当前值就找右结点继续遍历,如果当前值小于结点就继续找左结点遍历,直到相等以及遍历树为空时结束。
public Node search(int e) {
Node search = root;
while (search != null) {
if (search.val == e) {
return search;
}
if (search.val > e) {
search = search.left;
} else {
search = search.right;
}
}
return null;
}接下来就是最难的一部分删除节点
2.4 删除节点
为什么删除节点会难一点呢,主要原因是我们在存储时把各个节点链到了一起,当你删除其中某一个节点,随之而来的父节点,左右节点的关系都要改变。
2.4.1 删除单节点场景
假如删除的是一个单节点,没有左或右节点时是一个场景,例如图二,删除14,剩下右子节点18,它需要怎样的变化?
图二
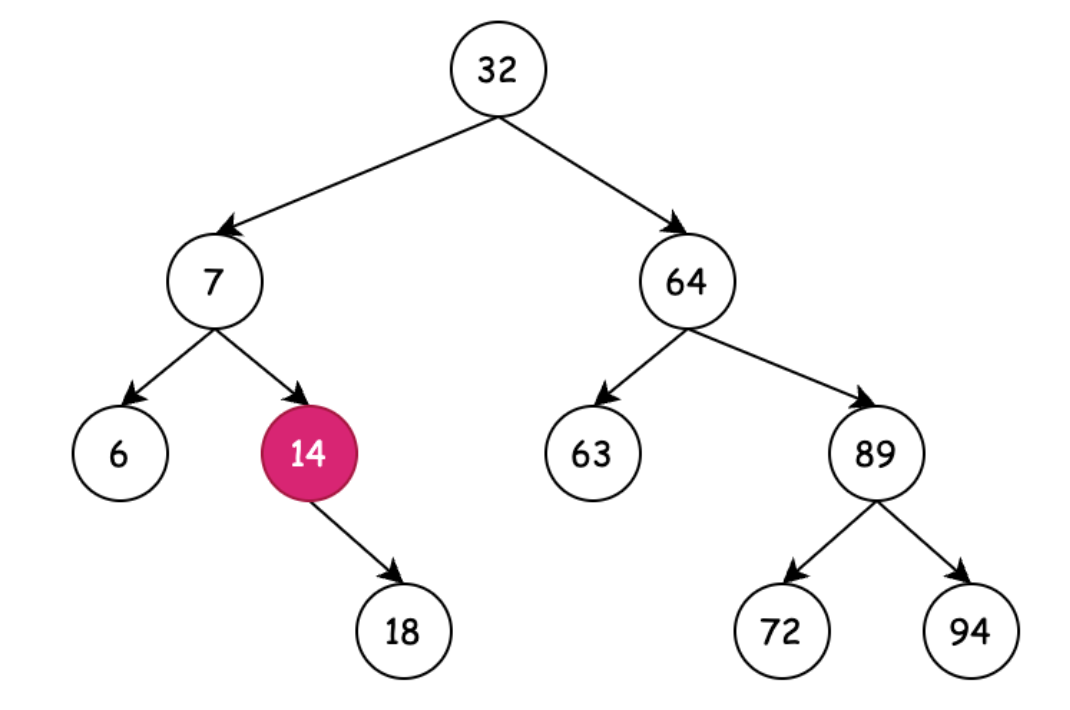
发现待删除节点有一个右节点18,将18放入待删除节点14的位置
将14的父节点的右节点替换18即可,如图三
图三
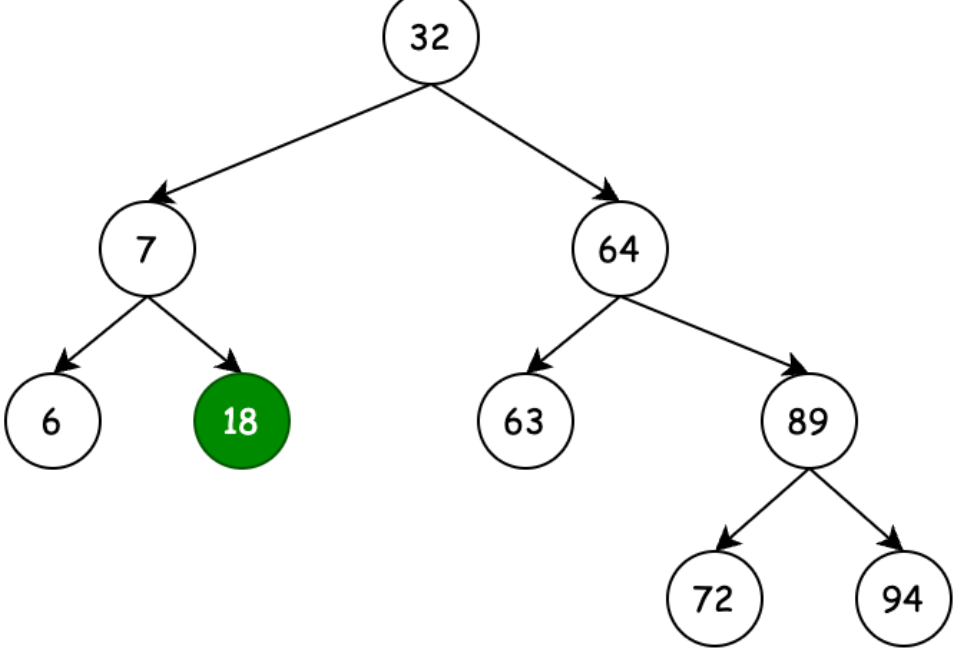
2.4.2 删除节点时有双节点场景
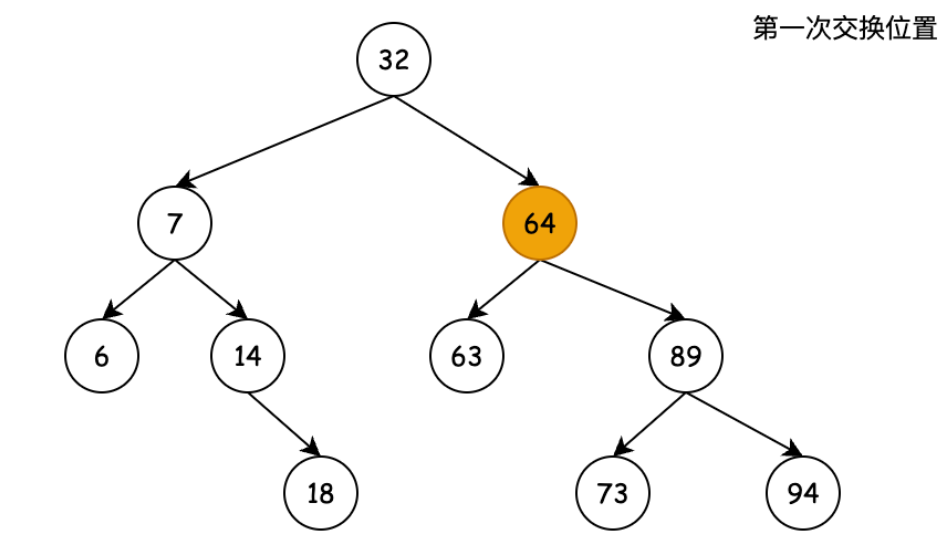
要被删除的节点有双节点,那么我们就需要根据当前待删除节点第一个右子节点找到待删除节点下子节点最小的值,来替换到待删除节点,使之成为依然有序的二叉树,之后就需要将对应的节点关系链条进行修改。
图四

替代节点要被挪走了,那么它的位置就需要子节点顶替
图五
将各个节点关系链条进行处理,使之成为一颗有序二叉树
图六
第一步,找到待删除节点第一个右子节点的左节点,只要有左节点一直循环,找到最左得到如图四找到72
第二步,将72和73传入到transplant()转移方法中,将关系进行更改,首先将89的左节点改为原来72的右节点也就是73,然后将73的父结点改为原72的父节点为89,这样底下这个关系对了,如图五。
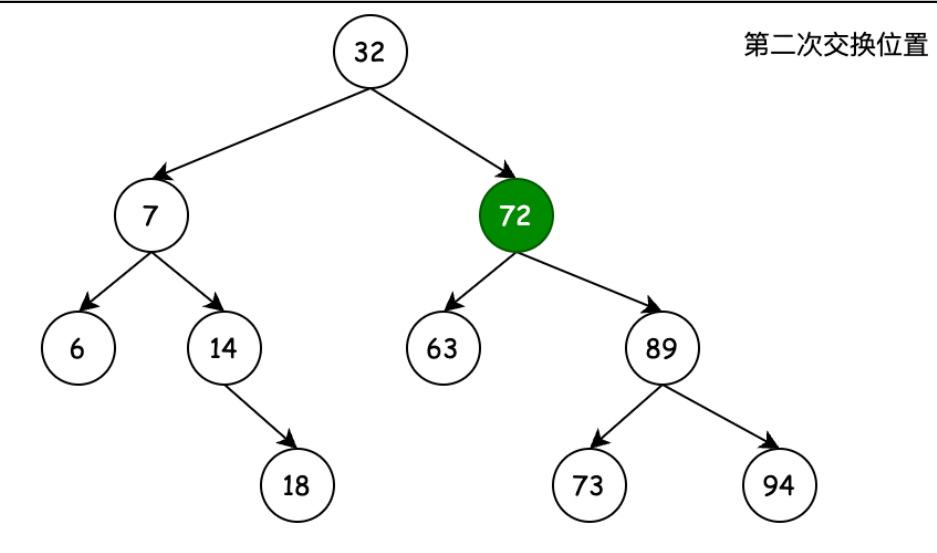
第三步,将72的的右节点,改为待删除节点64的右节点89,将72的父节点的右结点改为72
将64和72传入到transplant()转移方法,将64的父节点的右节点改为72,将72的父亲节点改为64的父亲节点32
继续更改,将72的左节点改为64的左节点
将72的左节点的父节点改为72,所有的关联都已经改完,结束
// 根据索引找到待删除的节点数据
public Node delete(int e) {
// 查找要删除的节点
Node delNode = search(e);
if (null == delNode) {
return null;
}
return delete(delNode);
}
// 删除并转移链条关系
public Node delete(Node delNode) {
Node result = null;
if (delNode.left == null) {
// 左节点为空,那就把待删除结点右节点传递进去
result = transplant(delNode, delNode.right);
} else if (delNode.right == null) {
// 相反,右节点为空,将左节点代入进去
result = transplant(delNode, delNode.left);
} else {
// 待删除的左右节点都存在,所以需要找到最小值替换待删除节点
Node minNode = getMiniNode(delNode.right);
// 判断右侧树最小的节点的父节点是否不等于待删除节点,才进行节点替换
if (minNode.parent != delNode) {
// 交换位置,用miniNode右节点,替换miniNode
transplant(minNode, minNode.right);
// 把miniNode 提升父节点,设置右子树并进行挂链。替代待删节点
minNode.right = delNode.right;
minNode.right.parent = minNode;
}
// 此时交换位置删除节点
transplant(delNode, minNode);
// 把miniNode 提升到父节点,设置左子树并挂链
minNode.left = delNode.left;
minNode.left.parent = minNode;
result = minNode;
}
return result;
}
// 找到左节点最小值
private Node getMiniNode(Node node) {
while (node.left != null) {
node = node.left;
}
return node;
}
/**
* 主要判断然后更改根节点
* 待删除节点的父节点的左节点
* 待删除的节点的父亲的右节点
* 新选举的节点的父结点改成待删除的父节点
* */
private Node transplant(Node delNode, Node addNode) {
if (delNode.parent == null) {
this.root = addNode;
// 判断删除元素是左/右节点,将要添加的节点赋值到待删除节点的父节点的左/右节点
} else if (delNode.parent.left == delNode) {
delNode.parent.left = addNode;
} else {
delNode.parent.right = addNode;
}
// 设置新节点的父节点
if (addNode != null) {
addNode.parent = delNode.parent;
}
return addNode;
}全部代码如下
public class BinarySearchTree {
public class Node {
// 当前值
private Integer val;
// 父节点
private Node parent;
// 左节点
private Node left;
// 右节点
private Node right;
public Node(int val, Node parent, Node left, Node right) {
this.val = val;
this.left = left;
this.right = right;
this.parent = parent;
}
}
private Node root;
/*
* 32
* 7 64
* 6 14 63 89
* 18 72
* 我们先来看一下,它的规律是,左边的树不论是那个节点都比自己的根节点小,右节点都比根节点大
* 按总的一个根节点(例:32)来说,它的所有左节点都比根节点小,所有的右节点都比根节点大
* 这样的一个规律,我们就可以统一判断当前值是否小于或大于循环比对的值,小于放左边,大于放右边即可
* 如果有值则继续循环找空,直到没有值进行各个父节点给左右节点存储当前值即可
*
* 1.假如存储32因为是第一个值直接存储到节点中
* 2.假如存储7需要比对32的值发现7比32小放左边,然后创建新的节点,当前节点为7,父节点为32,存储在32的左边
* 3.假如存储64需要循环比对,先比对32发现比32大放右边,32的右边没有值为空,此时创建新的节点,当前节点为64,父节点为32,存储32的右边
* 4.假如存储6需要循环比对,比对32的值发现6比32小放左边,左边此时有7,所以赋值临时变量,再次进入循环7比对6,发现7比6大,放左边
* 此时7的左边是空,这时退出循环,创建新节点(当前节点为6,父节点为7),存储在7的左边
* 5.此时存储14,需要循环比对,比对32的值发现14比32小,找左边,左边发现有值为7,再次赋值临时变量,进入循环7比14,7小于
* 14,找到7的右边发现为空,退出循环创建新节点(当前节点为14,父节点为7),存储7的左边
* */
// 32-7-64-6-14-63-89
public Node insert(int e) {
// 没有根元素添加根元素
if (root == null) {
root = new Node(e, null, null, null);
return root;
}
Node parent = root;
Node search = root;
// 循环取左右元素,看当前要存储的元素要挂到哪个节点下
while (search != null) {
// 将每一次判断完的左右元素赋值给parent,这样退出循环时就可以再他的左右节点挂值
parent = search;
// 判断值大小即可知道左节点右节点,取出有值则循环,没值则退出循环
if (search.val > e) {
search = search.left;
} else {
search = search.right;
}
}
Node newNode = new Node(e, parent, null, null);
if (parent.val > newNode.val) {
parent.left = newNode;
} else {
parent.right = newNode;
}
return parent;
}
public Node search(int e) {
Node search = root;
while (search != null) {
if (search.val == e) {
return search;
}
if (search.val > e) {
search = search.left;
} else {
search = search.right;
}
}
return null;
}
// 根据索引找到待删除的节点数据
public Node delete(int e) {
// 查找要删除的节点
Node delNode = search(e);
if (null == delNode) {
return null;
}
return delete(delNode);
}
// 删除并转移链条关系
public Node delete(Node delNode) {
Node result = null;
if (delNode.left == null) {
Integer s = null;
if (delNode.right != null) {
s = delNode.right.val;
}
result = transplant(delNode, delNode.right);
System.out.println(delNode.val + "的左节点为空,传入右节点为:" + s);
} else if (delNode.right == null) {
Integer s = null;
if (delNode.left != null) {
s = delNode.left.val;
}
System.out.println(delNode.val + "的右节点为空,传入左节点为:" + s);
result = transplant(delNode, delNode.left);
} else {
System.out.println("当前节点:" + delNode.val + "待删除节点的左右树都有");
Node minNode = getMiniNode(delNode.right);
// 判断右侧树最小的节点的父节点是否不等于待删除节点,才进行节点替换
if (minNode.parent != delNode) {
System.out.println("替换:" + minNode.val + "不等于当前待删除的节点,minNode:" + minNode.val + ",delNode:" + delNode.val);
transplant(minNode, minNode.right);
minNode.right = delNode.right;
System.err.println("替换:" + minNode.val + "的右节点赋值为" + delNode.val + "的右节点(" + delNode.right.val + ")");
minNode.right.parent = minNode;
System.err.println("替换:" + minNode.val + "的右节点的父节点赋值为" + minNode.val + "的节点");
}
transplant(delNode, minNode);
minNode.left = delNode.left;
System.err.println("替换:" + minNode.val + "的左节点赋值为delNode的左节点:" + delNode.left.val);
minNode.left.parent = minNode;
System.err.println("替换:" + minNode.val + "的左节点的父节点赋值为minNode(" + minNode.val + ")");
result = minNode;
}
return result;
}
// 找到左节点最小值
private Node getMiniNode(Node node) {
while (node.left != null) {
node = node.left;
}
System.out.println("找到当前节点右树最小的minNode节点:" + node.val);
return node;
}
/**
* 主要判断然后更改根节点
* 待删除节点的父节点的左节点
* 待删除的节点的父亲的右节点
* 新选举的节点的父结点改成待删除的父节点
* */
private Node transplant(Node delNode, Node addNode) {
if (delNode.parent == null) {
this.root = addNode;
System.err.println("替换:" + delNode.val + "的父节点为空,把root根置为:" + addNode.val);
} else if (delNode.parent.left == delNode) {
Integer s = null;
if (addNode != null) {
s = addNode.val;
}
delNode.parent.left = addNode;
System.err.println("替换:" + delNode.parent.left.val + "的父节点的左节点==" + delNode.val + ",把" + delNode.val + "的父节点的左节点置为:" + s);
} else {
delNode.parent.right = addNode;
System.err.println("替换:" + delNode.val + "的父节点的右节点置为:" + addNode.val);
}
if (addNode != null) {
addNode.parent = delNode.parent;
Integer s = null;
if (delNode.parent != null) {
s = addNode.parent.val;
}
System.err.println("替换:" + addNode.val + "父节点不为空时,把" + addNode.val + "的父节点置为" + s);
}
return addNode;
}
}main方法测试一下,
先插入节点,再删除节点,咱们看一下控制台输出
public static void main(String[] args) {
BinarySearchTree binarySearchTree = new BinarySearchTree();
binarySearchTree.insert(32);
binarySearchTree.insert(7);
binarySearchTree.insert(64);
binarySearchTree.insert(6);
binarySearchTree.insert(14);
binarySearchTree.insert(63);
binarySearchTree.insert(89);
binarySearchTree.insert(18);
binarySearchTree.insert(72);
Node node = binarySearchTree.search(14);
System.out.println(node.val);
System.out.println(" ");
System.out.println("删除7: ");
Node noded32 = binarySearchTree.delete(7);
}删除7控制台打印如下:

接下来你们自己去验证,删除单节点左/单节点右,调试熟悉,感受魅力,哈哈