【零基础】学python数据结构与算法笔记11

news2024/11/18 11:17:33

文章目录

  • 前言
  • 65.树的概念
  • 66.树的实例：模拟文件系统
  • 67.二叉树的概念
  • 68.二叉树的遍历
  • 69.二叉搜索树的概念。
  • 70.二叉搜索树：插入
  • 71.二叉搜索树：查询
  • 72.二叉搜索树：删除
  • 73.二叉搜索树：删除实现
  • 总结

前言

学习python数据结构与算法，学习常用的算法，
b站学习链接

65.树的概念

之前讲推排序时学过这个树的概念
【零基础】学python数据结构与算法笔记4
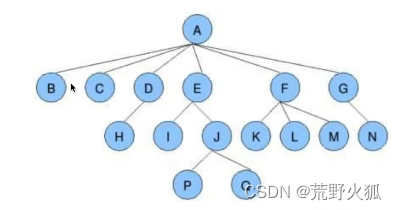
这个树，我单拎出来一个节点就是一个树，B是一个子树，EIJPQ也是一个子树。

在这里插入图片描述

66.树的实例：模拟文件系统

模拟linux系统里的文件系统
Linux 文件与目录管理
命令mkdir
ls
cd
先建立树的一个节点
然后用树实现文件系统，一个文件夹下有几个文件夹。
在这里插入图片描述
进入usr文件夹下，下有python一个子文件夹

在这里插入图片描述
…/ 返回上一级根目录，[var/, bin/, usr/]
在这里插入图片描述

67.二叉树的概念

二叉树链式存储：将二叉树的节点定义为一个对象，节点之间通过类似链表的链接方式来连接。
之前堆排序里讲的是完全二叉树，只有右边少数，这里讲的不是完全二叉树。
比方说这样一颗树
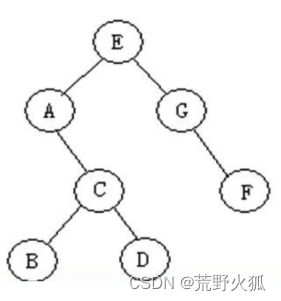
在这里插入图片描述
只有左孩子和右孩子，如下定义，找根节点的左孩子的右孩子的数据，为C
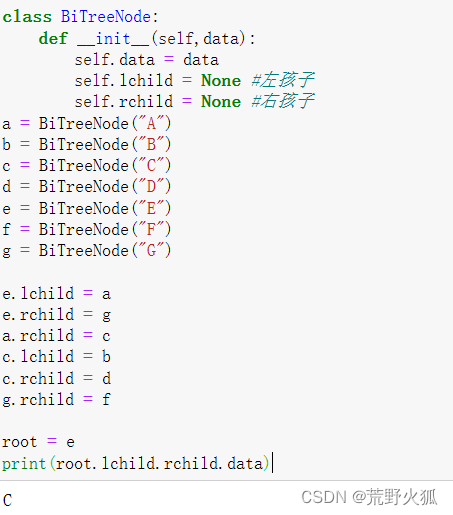
在这里插入图片描述

68.二叉树的遍历

二叉树遍历方式有4种
前序遍历：EACBDGF
中序遍历：ABCDEGF
后序遍历：BDCAFGE
层次遍历：EAGCFBD

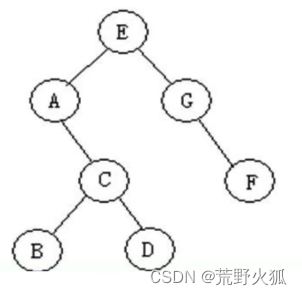
在这里插入图片描述
前序遍历
是写打印根节点，再打印左孩子，再打印右孩子吗，用递归写出

在这里插入图片描述
先是根节点E,再是左节点A,A没有左节点然后右节点C,然后左节点B,右节点D,左树遍历完了然后右树，先是G，没有左节点，最后右节点F。
在这里插入图片描述
中序遍历
先是左孩子，再是根节点，再是右孩子，根节点在中间，和前序遍历只是顺序不同

在这里插入图片描述
先是左孩子A然后看CBD这个树的左孩子是B,然后根节点C,然后右节点D,再是整个树的根节点E,最后右节点G,再是F

在这里插入图片描述
后序遍历
先是左孩子，然后右孩子，最后根节点。

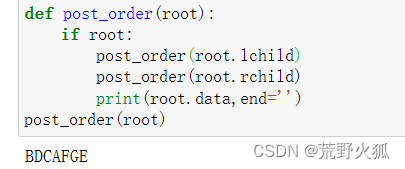
在这里插入图片描述
先看左孩子这一侧ACBD子树，再看BCD子树，先是左孩子B,再是右孩子D,最后根节点C,然后ACBD的根节点A,看GF树，左孩子没有，右孩子F,根节点G,最后大树的根节点E。

在这里插入图片描述
这三种面试的时候经常会考，还会考一种，知道前序排序和中序排序画树和后序排序，还有知道中序排序和后序排序画树和前序排序。

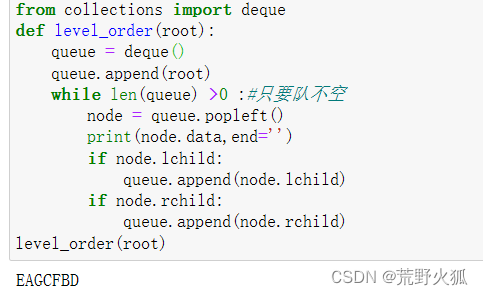
层次排序
按照一层一层打印，不是二叉树也可以按照此方法
思路如下，使用队列，先进队根节点，然后出根节点，如果有左孩子或者右孩子就进队，然后再出此时的根节点，进左右孩子，直到队出完，就遍历完了。就和之前学的广度优先搜索差不多。【零基础】学python数据结构与算法笔记9中的队列实现迷宫问题
在这里插入图片描述

69.二叉搜索树的概念。

二叉搜索树是一颗二叉树且满足性质：设x是二叉树的一个节点。如果y是x左子树的一个节点，那么y.key<=x.key;如果y是x右子树的一个节点，那么y.key>=x.key。
二叉搜索树的操作：查询、插入、删除
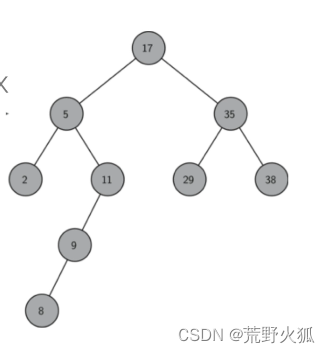
在这里插入图片描述
比方说查11，先看17，11比17小，看17的左子树5，11比5大看5的右子树，是11找到。
比方说插入32，先看17，32比17大，看右子树36，比36小看29，比29大所以在29的右子树上。
查询和插入都是折半的操作，所以大概是logn,删除操作比较复杂，待会说。

70.二叉搜索树：插入

根据刚刚所说写出二叉搜索树的插入

#二叉搜索树
class BiTreeNode:
    def __init__(self,data):
        self.data = data
        self.lchild = None #左孩子
        self.rchild = None #右孩子
        self.parent = None  
class BST:#binary search tree
    def __init__(self,li= None):
        self.root = None
        if li:
            for val in li:
                self.insert_no_rec(val)
                #self.root = self.insert(self.root,val) 
    def insert(self,node,val): #递归写法
        if not node: #如果没有节点了就插入
            node = BiTreeNode(val)
        elif val < node.data:
            node.lchild = self.insert(node.lchild,val)
            node.lchild.parent = node
        elif val > node.data:
            node.rchild = self.insert(node.rchild,val)
            node.rchild.parent = node
            #如果是相等则不操作。
        return node
    def insert_no_rec(self,val):#非递归写法
        p = self.root
        if not p:#如果是空树
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:  #如果左子树存在，则根节点为这颗左树的根
                    p =p.lchild 
                else:#左孩子不存在,就插到这个位置上
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return 
    def pre_order(self,root):
        if root:
            print(root.data,end=",")
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)
    def in_order(self,root):
        if root:
            self.in_order(root.lchild)
            print(root.data,end=",")
            self.in_order(root.rchild)
    def post_order(self,root):
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data,end=',')

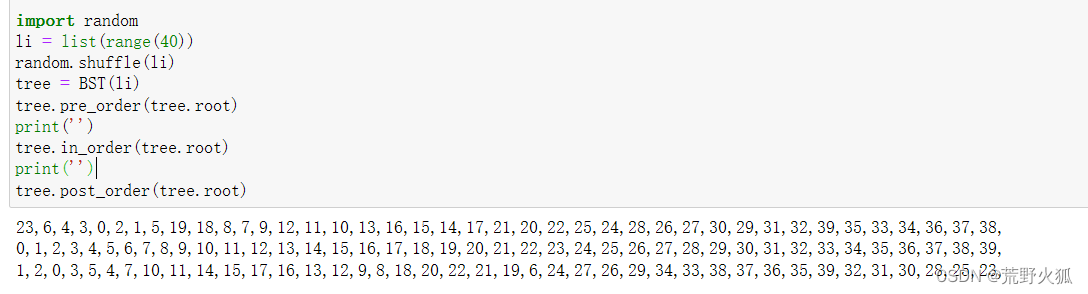
发现中序遍历是升序的排序，因为正好符合二叉搜索树的定义，左边最小，中间根大，右边最大。
在这里插入图片描述

71.二叉搜索树：查询

递归算法比不递归的慢，也比较难理解。

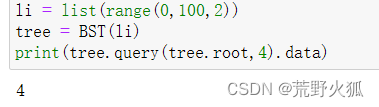
在这里插入图片描述
递归形式
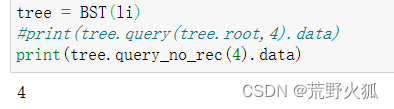
在这里插入图片描述
非递归形式
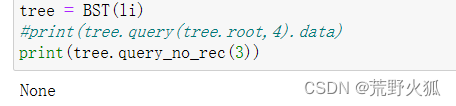
在这里插入图片描述
查3就查不到
在这里插入图片描述

72.二叉搜索树：删除

分三种情况讨论
1.如果要删除的节点是叶子节点：直接删除

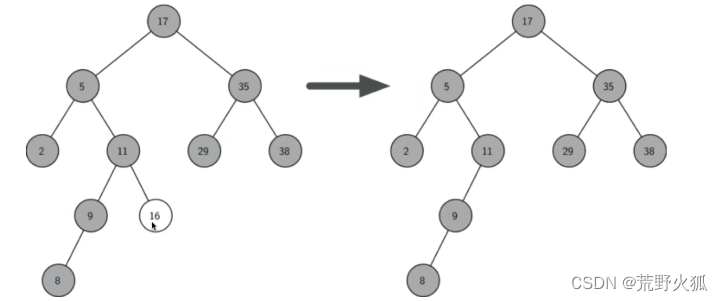
在这里插入图片描述
2.如果删除的节点只有一个孩子：将此节点的父亲与孩子连接，然后删除该节点
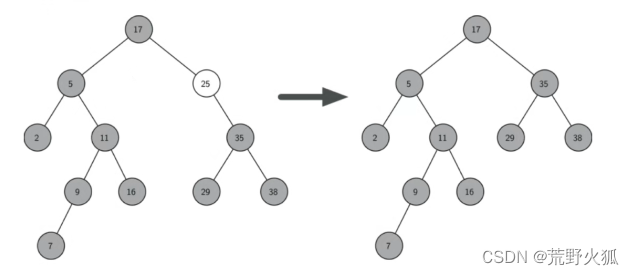
在这里插入图片描述
有一个特殊情况，假设现在只有17，35，29，38四个节点，要删除的是这个17这个根，那就需要重新更新根节点。
3.如果要删除的节点有两个孩子：将其右子树的最小节点（该节点最多有一个右孩子）删除，并替换当前节点。（或者说是左子树的最大节点删除并替换）

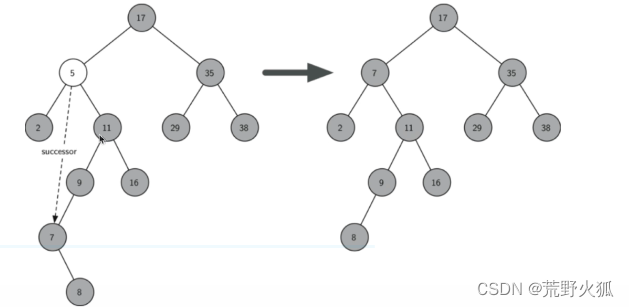
在这里插入图片描述

73.二叉搜索树：删除实现

先分情况写__remove_node_1
__remove_node_21
__remove_node_21
第三种写在delete里，
第二种实现有点像双链表的删除实现，画个图会好理解点。

总的代码如下

#二叉搜索树
class BiTreeNode:
    def __init__(self,data):
        self.data = data
        self.lchild = None #左孩子
        self.rchild = None #右孩子
        self.parent = None  
class BST:#binary search tree
    def __init__(self,li= None):
        self.root = None
        if li:
            for val in li:
                self.insert_no_rec(val)
                #self.root = self.insert(self.root,val) 
    def insert(self,node,val): #递归写法
        if not node: #如果没有节点了就插入
            node = BiTreeNode(val)
        elif val < node.data:
            node.lchild = self.insert(node.lchild,val)
            node.lchild.parent = node
        elif val > node.data:
            node.rchild = self.insert(node.rchild,val)
            node.rchild.parent = node
            #如果是相等则不操作。
        return node
    def insert_no_rec(self,val):
        p = self.root
        if not p:#如果是空树
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:  #如果左子树存在，则根节点为这颗左树的根
                    p =p.lchild 
                else:#左孩子不存在,就插到这个位置上
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return 
    def query(self,node,val): #递归写法
        if not node:
            return None
        if node.data <val:#val大，找右节点
            return self.query(node.rchild,val)
        elif node.data >val:
            return self.query(node.lchild,val)
        else:#如果找到了
            return node 
    def query_no_rec(self,val):
        p = self.root
        while p:
            if p.data <val: #val大
                p = p.rchild
            elif p.data >val:
                p = p.lchild
            else: #找到了
                return p
        return None#找不到 return None
    def __remove_node_1(self,node): #加两下划线表示是类的内置函数
        #情况1：node是叶子节点
        if not node.parent: #如果删除的是根节点
            self.root = None
        if node ==node.parent.lchild:  #node是它父亲的左孩子
            node.parent.lchild  = None #删除左节点
        else:  #右孩子
            node.parent.rchild = None
    def __remove_node_21(self,node):
        #情况2.1：node只有一个左孩子
        if not node.parent: #如果删除的node是根节点
            self.root = node.lchild  #先连到根节点
            node.lchild.parent = None #再把自己删了
        elif node == node.parent.lchild: #如果删除的node是左孩子
            node.parent.lchild = node.lchild #把自己的左孩子连到自己根节点的左孩子上
            node.lchild.parent = node.parent #把自己的根节点连到自己左孩子的父节点上
        else:  #如果删除的node是右孩子
            node.parent.rchild = node.lchild #把自己的左孩子连到自己根节点的右孩子上
            node.lchild.parent = node.parent 
    def __remove_node_22(self,node):
        #情况2.2：node只有一个右孩子
        if not node.parent: #如果删除的node是根节点
            self.root = node.rchild  #先连到根节点
            node.lchild.parent = None #再把自己删了
        elif node == node.parent.lchild: #如果删除的node是左孩子
            node.parent.lchild = node.rchild #把自己的右孩子连到自己根节点的左孩子上
            node.rchild.parent = node.parent #把自己的根节点连到自己右孩子的父节点上
        else:  #如果删除的node是右孩子
            node.parent.rchild = node.rchild #把自己的右孩子连到自己根节点的右孩子上
            node.rchild.parent = node.parent 
    def delete(self,val):
        if self.root:  #不是空树
            node = self.query_no_rec(val)
            if not node: #不存在
                return False
            if not node.lchild and not node.rchild:  #1.叶子节点
                self.__remove_node_1(node)
            elif not node.rchild:  #2.1只有一个左孩子
                self.__remove_node_21(node)
            elif not node.lchild: #2.2
                self.__remove_node_22(node)
            else: #3.两个孩子都有  #将其右子树的最小节点（最多有一个右孩子）删除，并替换当前节点
                min_node = node.rchild
                while min_node.lchild:#左边的小
                    min_node = min_node.lchild #一直找到最小的即最后一个左孩子
                node.data = min_node.data #把数据赋给node
                # 然后删除min_node
                if min_node.rchild: #如果只有一个右孩子
                    self.__remove_node_22(min_node)
                else: #或者没有
                    self.__remove_node_1(min_node)            
    def pre_order(self,root):
        if root:
            print(root.data,end=",")
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)
    def in_order(self,root):
        if root:
            self.in_order(root.lchild)
            print(root.data,end=",")
            self.in_order(root.rchild)
    def post_order(self,root):
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data,end=',')

最后成功删除
在这里插入图片描述

总结

学习了二叉树和二叉搜索树的基本实现。

文章目录

  • 前言
  • 65.树的概念
  • 66.树的实例：模拟文件系统
  • 67.二叉树的概念
  • 68.二叉树的遍历
  • 69.二叉搜索树的概念。
  • 70.二叉搜索树：插入
  • 71.二叉搜索树：查询
  • 72.二叉搜索树：删除
  • 73.二叉搜索树：删除实现
  • 总结

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/163819.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

中本聪是个贪婪的矿工吗？

中本聪是个贪婪的矿工吗？

对可能是中本聪的实体所表现出的挖矿行为的技术分析。文 | Jameson Lopp. 原标题&#xff1a;Was Satoshi a Greedy Miner?. 2022/9/16.* * *如果你在加密生态系统中待了足够久的时间&#xff0c;那么你无疑会听到这样的论点&#xff0c;即某些项目的代币分配不公平&#xff0…
阅读更多...
Windous注册表+c#操作

Windous注册表+c#操作

下面将会分享注册表的基础知识及C# 读写注册表的方法 了解注册表 注册表&#xff08;英语&#xff1a;Registry&#xff0c;中国大陆译作注册表&#xff0c;台湾、港、澳译作登录档&#xff09;是Microsoft Windows操作系统和其应用程序中的一个重要的层次型数据库&#xff0…
阅读更多...
关于计算机网络,你需要知道的一些常识

关于计算机网络,你需要知道的一些常识

最近闲着没啥事翻开之前大学时候谢希仁老师第7版的《计算机网络》这本书,结果发现了一些之前没有发现的常识。 首先是互联网与互连网的区别,一般我们常说的互联网是Internet,是指因特网,其起源于阿帕网ARPANT。或许很多读者看到这里就觉得有什么秘密可言,不都是常识了吗?看你大…
阅读更多...
如何在Vue3+js项目（脚手架）中使用（下载安装及运行）element-plus以及解决使用过程中遇到的问题

如何在Vue3+js项目（脚手架）中使用（下载安装及运行）element-plus以及解决使用过程中遇到的问题

文章目录 &#x1f4cb;前言 &#x1f3af;关于 ElementUI 框架描述 &#x1f9e9;设计原则 1️⃣一致 Consistency 2️⃣反馈 Feedback 3️⃣效率 Efficiency 4️⃣可控 Controllability &#x1f9e9;环境支持 &#x1f3af;安装element-plus &#x1f9e9;遇到的问…
阅读更多...
【随笔】博客质量分计算，如何让自己的博客脱颖而出，也许文章能够给你答案

【随笔】博客质量分计算，如何让自己的博客脱颖而出，也许文章能够给你答案

作者&#xff1a;小5聊 简介&#xff1a;一只喜欢全栈方向的程序员&#xff0c;专注基础和实战分享&#xff0c;欢迎咨询&#xff0c;尽绵薄之力答疑解惑&#xff01; 公众号&#xff1a;有趣小馆&#xff0c;一个有趣好玩的关键词回复互动式公众号&#xff0c;欢迎前来体验 1、…
阅读更多...
TSF微服务治理实战系列（四）——服务安全

TSF微服务治理实战系列（四）——服务安全

一、导语 **道路千万条&#xff0c;安全第一条。治理不规范&#xff0c;老板两行泪”。**当企业从单体架构逐渐转向微服务架构时&#xff0c; 服务安全 的需求也随之分散到了整个微服务体系的各个部分中。这就需要构建一套配置活、成本低的安全防控体系&#xff0c;覆盖请求链…
阅读更多...
基于javaweb(springboot)城市地名地址信息管理系统设计和实现

基于javaweb(springboot)城市地名地址信息管理系统设计和实现

基于javaweb(springboot)城市地名地址信息管理系统设计和实现 博主介绍&#xff1a;5年java开发经验&#xff0c;专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java毕设项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文…
阅读更多...
日志门面和日志框架(SpringBoot日志实现)

日志门面和日志框架(SpringBoot日志实现)

一、Springboot日志实现简介 SpringBoot是现今市场上最火爆用来简化spring开发的框架&#xff0c;springboot日志也是开发常用的日志系统。SpringBoot默认就是使用SLF4J作为日志门面&#xff0c;Logback作为日志实现来记录日志。 二、application.yml修改日志相关的配置 appl…
阅读更多...
Spring入门-IOC/DI相关配置与使用(1)

Spring入门-IOC/DI相关配置与使用(1)

文章目录Spring入门1&#xff0c;Spring介绍1.1 为什么要学?1.2 学什么?1.3 怎么学?2&#xff0c;Spring相关概念2.1 初识Spring2.1.1 Spring家族2.1.2 了解Spring发展史2.2 Spring系统架构2.2.1 系统架构图2.2.2 课程学习路线2.3 Spring核心概念2.3.1 目前项目中的问题2.3.…
阅读更多...
修改RT-Thread 的启动流程，实现显式调用rtthread_startup

修改RT-Thread 的启动流程，实现显式调用rtthread_startup

一、STM32 单片机的启动流程 单片机上电后&#xff0c;会首先执行定义在startup 文件 中的Reset_Handler 函数&#xff0c;Reset_Handler 函数会首先执行SystemInit 函数&#xff0c;执行完之后&#xff0c;再执行我们常见的main 函数。 二、RT-Thread 启动函数是怎么被调用的…
阅读更多...
什么是最少知识原则？-外观模式

什么是最少知识原则？-外观模式

外观模式将一个或数个类的复杂的一切都隐藏在背后&#xff0c;只显露出一个干净美好的外观。 构建自己的家庭影院 //打开爆米花机&#xff0c;开始爆米花 popper.on(); popper.pop();//调整灯光亮度 lights.dim(10);//把屏幕放下 screen.down();//打开投影仪 projector.on();…
阅读更多...
【阶段三】Python机器学习32篇：机器学习项目实战：关联分析的基本概念和Apriori算法的数学演示

【阶段三】Python机器学习32篇：机器学习项目实战：关联分析的基本概念和Apriori算法的数学演示

本篇的思维导图： 关联分析模型：Apriori算法 关联分析的基本概念和Apriori算法 关联分析是数据挖掘中一种简单而实用的技术，它通过深入分析数据集，寻找事物间的关联性，挖掘频繁出现的组合，并描述组合内对象同时出现的模式和规律。例如，对超市购物的数据进行关联…
阅读更多...
缓存Cache-Control

缓存Cache-Control

可缓存性指定哪些地方可以缓存publichttp请求返回的过程中&#xff0c;http请求返回的内容所经过的任何路径包括&#xff1a;中间的代理服务器&#xff0c;发出请求的客户端浏览器&#xff0c;都可以对返回的内容进行缓存。private发起请求的浏览器可以缓存。no-cache任何节点都…
阅读更多...
【程序员高效率工具】PlantUML —— 使用代码快速绘制时序图、思维导图

【程序员高效率工具】PlantUML —— 使用代码快速绘制时序图、思维导图

本篇思维导图 前言 不管是在工作还是学习&#xff0c;特别是在项目计划初期&#xff0c;我们需要画大量的图将工作内容、项目方案等进行可视化描述&#xff0c;包括但不限于时序图、类图、思维导图等等。 但是对于不经常画图&#xff0c;或者经常使用键盘的孩子&#xff0c;手…
阅读更多...
VMware三种网络模式的摸索

VMware三种网络模式的摸索

VMware三种网络模式的摸索 文章目录VMware三种网络模式的摸索前言一、桥接模式简要描述拓扑图展示配置测试优缺点二、NAT模式简要描述拓扑图展示配置测试优缺点三、仅主机模式简要描述拓扑图展示配置测试优缺点3.总结前言 注意&#xff1a;所有的测试请关闭虚拟机和主机的防火…
阅读更多...
微信小程序 - 实现手机号登录--授权并获取手机号保存至本地

微信小程序 - 实现手机号登录--授权并获取手机号保存至本地

详细代码请见文档最下方&#xff0c;仅供参考&#xff0c;更多需要请查看官方文档 一、 微信官方文档 | 获取手机号 这是服务端的 这是我们前端获取手机号需要给接口传递的两个参数 注意&#xff1a; 参数一&#xff1a;获取access_token需要用到小程序密钥&#xff0c;这个…
阅读更多...
你可能不知道的20个Git命令，但真的很实用

你可能不知道的20个Git命令，但真的很实用

如果您曾经浏览过git 手册&#xff08;或 run man git&#xff09;&#xff0c;那么您会注意到 git 的功能比我们大多数人每天使用的要多得多。很多这些命令都非常强大&#xff0c;可以让你的生活更轻松&#xff08;其他命令有点小众&#xff0c;但仍然很高兴知道&#xff09;。…
阅读更多...
QT-QStackedWidget多窗口应用

QT-QStackedWidget多窗口应用

前言&#xff1a; 多窗口应用&#xff0c;例如某微信&#xff0c;页面由1&#xff0c;2&#xff0c;3个布局组成。 1-基本流程 页面1控制页面2&#xff0c;通过选择页面1上的按钮或控件 页面2控制页面3&#xff0c;通过选择页面2上的按钮或控件 2-其中页面2中的页面很…
阅读更多...
100、【树与二叉树】leetcode ——105. 从前序与中序遍历序列构造二叉树+106. 从中序与后序遍历序列构造二叉树（C++版本）

100、【树与二叉树】leetcode ——105. 从前序与中序遍历序列构造二叉树+106. 从中序与后序遍历序列构造二叉树（C++版本）

106. 从中序与后序遍历序列构造二叉树 题目描述 原题链接&#xff1a;106. 从中序与后序遍历序列构造二叉树 解题思路 中序的特点&#xff1a;左中右&#xff0c;后序的特点&#xff1a;左右中。因此可通过后序序列找到中间结点&#xff0c;然后再根据中间结点&#xff0c;分…
阅读更多...
3、关键词与标识符

3、关键词与标识符

目录 一、关键词 二、标识符 一、关键词 C语言中有32个关键字&#xff1a; 注意&#xff1a;在C语言中&#xff0c;关键字是不允许作为标识符出现在程序中的。 二、标识符 C语言标识符的命名规则&#xff1a; &#xff08;1&#xff09;所有标识符必须由字母或下画线开头…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023