106. 从中序与后序遍历序列构造二叉树
题目描述
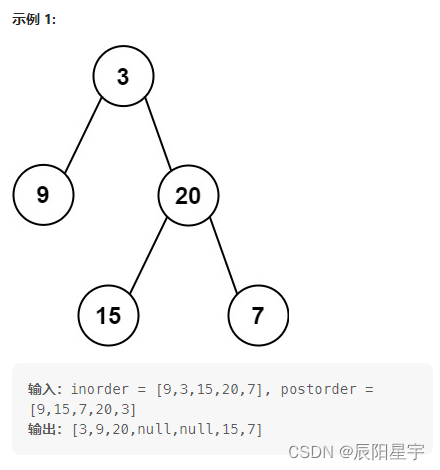

原题链接:106. 从中序与后序遍历序列构造二叉树
解题思路
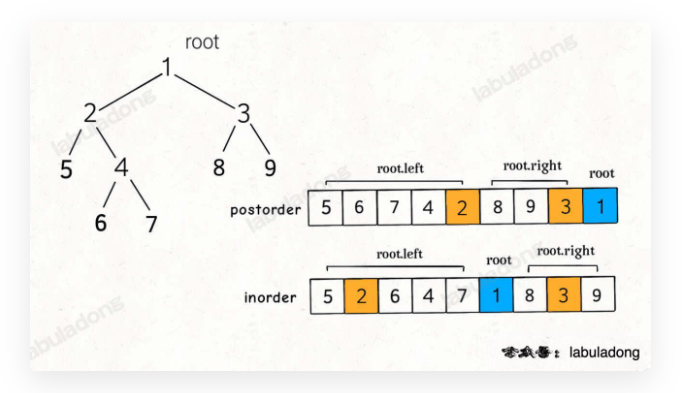
中序的特点:左中右,后序的特点:左右中。因此可通过后序序列找到中间结点,然后再根据中间结点,分割出中序的左子树和右子树。
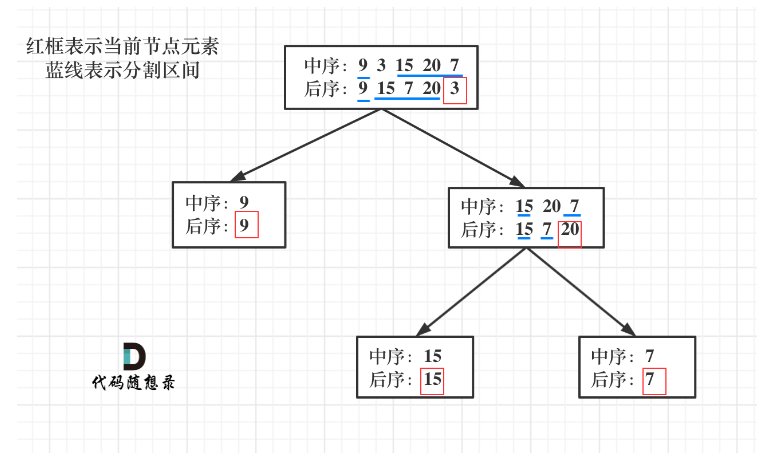
知道中序和后序,分割方式是:
(1)先判定数组大小,若为0,说明为空节点;
(2)若不为0,则获取中间结点(后序序列最后一个元素),作为结点元素。若数组大小为1,则返回
(3)若不为1,则根据这个结点元素分割先序序列。先找到中序序列的分割位置,然后分割出中序序列左子树和右子树。(此时要排除中序序列中的结点元素)
(4)根据 (3)中分割出的左右子树长度,再分割后序序列。分割出后序序列的左子树和右子树。(此时要排除后序序列的结点元素,也就是最后一个元素)。
(5)执行到最后,返回结点元素。(也就是最后一个栈弹出后,返回给main函数)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {
// 用后序遍历来分割,因此用后序遍历存储向量长度判定
int n = postorder.size();
// 1、当n为0时,说明为空结点
if(n == 0) return NULL;
// 2、获取后序遍历的最后一个结点,也就是中间结点
int value = postorder[n - 1];
TreeNode* node = new TreeNode(value);
// 当n为1时,说明分割出一个结点,返回
if(n == 1) return node;
// 3、分割中序序列
// 找到中间节点在先序遍历的位置,分割中序遍历序列
int delimiterIndex = 0;
while(inorder[delimiterIndex] != value) {
delimiterIndex++;
}
// 使用后续遍历的最后一个结点来分割中序遍历序列,此时不添加点为中序序列的中间结点
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end());
// 4、分割后序序列
// 使用中序遍历的分割出的左、右子树长度,来分割后续序列,此时未添加点在最后
postorder.resize(n - 1);
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
// 5、寻找左、右子树
// 使用中序的左和后序的左,继续分割出左子树
node->left = traversal(leftInorder, leftPostorder);
// 使用中序的右和后序的右,继续分割出右子树
node->right = traversal(rightInorder, rightPostorder);
return node;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.size() == 0|| postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
};
参考文章:106.从中序与后序遍历序列构造二叉树、东哥带你刷二叉树(构造篇)
105. 从前序与中序遍历序列构造二叉树
题目描述
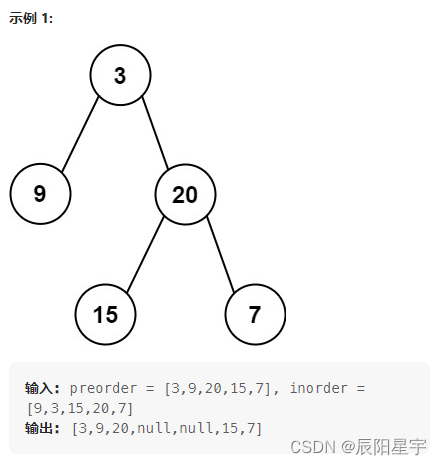

原题链接:105. 从前序与中序遍历序列构造二叉树
解题思路
解题思路与106. 从中序与后序遍历序列构造二叉树(递归法)类似。要注意一点是分割点和分割区间。
(1)分割点:先序序列的第一个元素
(2)中序序列分割区间:左子树:[begin,分割点),右子树:(分割点,end)
(3)先序序列分割区间:左子树:(begin,begin+中序左子树长度),右子树:[begin+中序左子树长度,end)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* traversal(vector<int>& preorder, vector<int>& inorder) {
// 每次用先序序列分割中序序列,以先序序列长度作为参考
int n = preorder.size();
// 1、当n为0时,说明为空结点
if(n == 0) return NULL;
// 2、获取先序序列的第一个元素,也就是中间结点
int value = preorder[0];
TreeNode* node = new TreeNode(value);
// 当为1时,说明为分割出的结点,返回
if(n == 1) return node;
// 3、分割中序序列
// 以先序序列的中间结点为分割点,找到中序序列的分割点位置
int delimiter = 0;
while(inorder[delimiter] != value) delimiter++;
vector<int> leftinorder(inorder.begin(), inorder.begin() + delimiter);
vector<int> rightinorder(inorder.begin() + delimiter + 1, inorder.end());
// 4、分割后序序列
// 以中序序列分割出的左右子树长度为参考,分割先序序列
// 这里要注意,分割时候要排除掉先序序列的第一个结点
vector<int> leftpreorder(preorder.begin() + 1, preorder.begin() + 1 + leftinorder.size());
vector<int> rightpreorder(preorder.begin() + 1 + leftinorder.size(), preorder.end());
// 5、进行向下分割左右子树
node->left = traversal(leftpreorder, leftinorder);
node->right = traversal(rightpreorder, rightinorder);
return node;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.size() == 0 || inorder.size() == 0) return NULL;
return traversal(preorder, inorder);
}
};