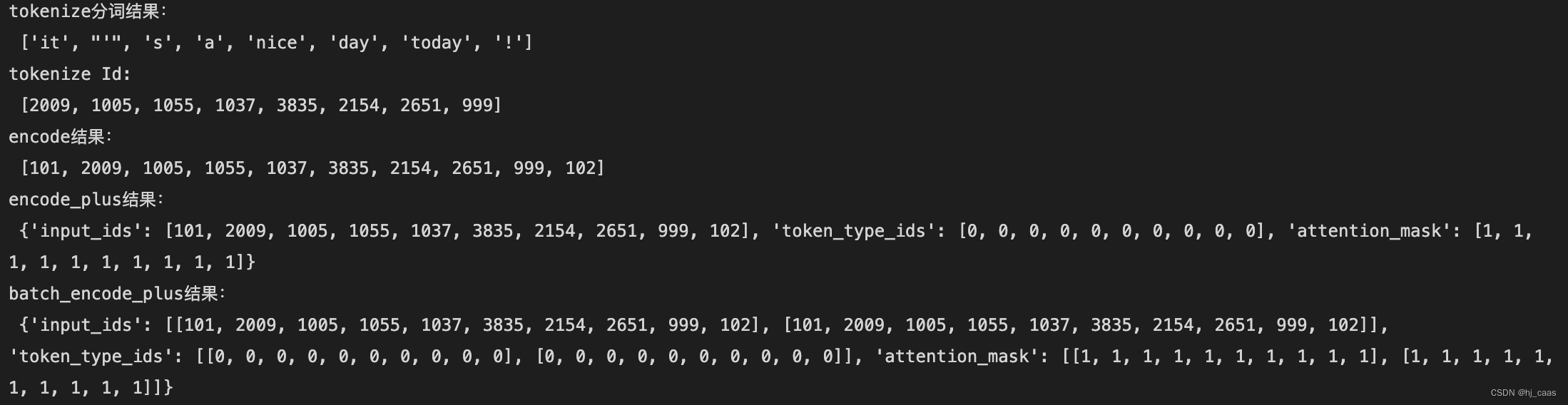
算法效率
- 数据结构
- 算法
- 时间复杂度
- 大O的渐进表示法
- 三种时间复杂度
- 几道例题
- 一.简单递归
- 二结合代码来判断时间复杂度
- 空间复杂度
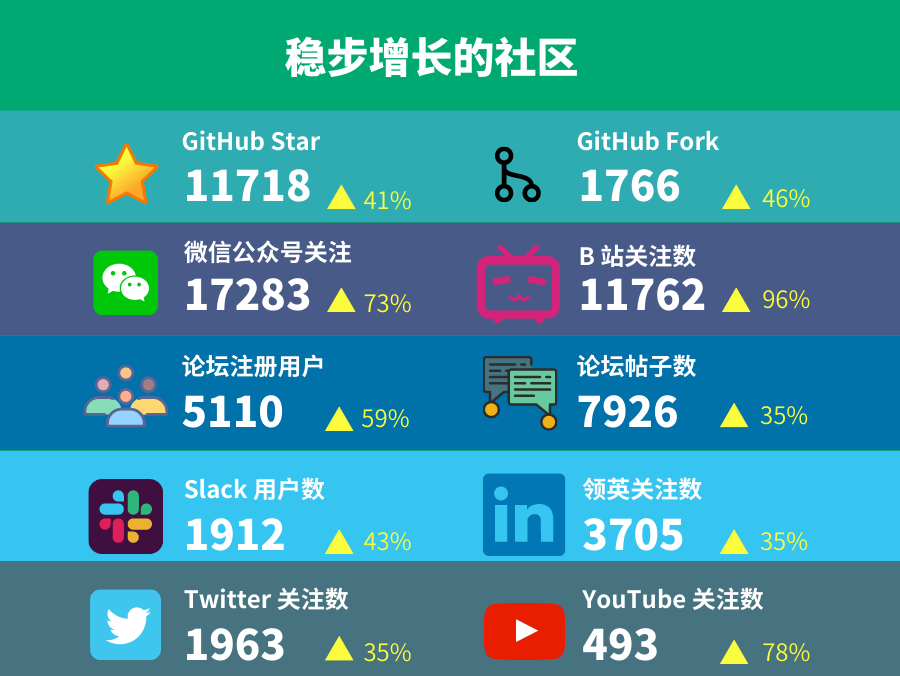
我们程序猿开始的时候肯定听了不少的:数据结构和算法,那么阿涛就给大家说说自己的拙见吧.
数据结构
数据结构就是我们用来组织数据的方式,比如我们可以把一组数据储存在数组中,那么我们就是以数组的形式组织了这一组数据,针对不同的数据,我们会根据自己的需求使用不同的数据结构,后面我都会一一给大家介绍.
算法
现在好像高学历的人都在卷算法,其实就我目前了解到的算法,也就是人家给你一组数据,你按照要求给人家返回了一组数据,这就是广义的,我们都能接触到的算法实例,当然更加具体的详细的就需要我和大家日后深入地去学习了.
话说回来,我们通常都会把数据结构和算法二者放在一起去讨论,这是因为这两者之间是相辅相成的,不可能说你一个精通数据结构的人一点算法不懂,反之也是一个道理,那么这篇博客主要是给我们学习后面的集合类做出一个铺垫,所谓集合类就是有一个我们上学时期学过的集合的概念,里面存放的是好多好多的数据结构.
我们学习一切的一切的目的,往小了说就是为了能找到一份好的offer,往深了说,不就是为了提升自己,让自己成为一名优秀的程序猿码?那么我们通常评判一个程序猿的最基本手段就是看这个程序猿的代码写的怎么样:
同样的一个程序,你写的代码比别人的运行的快,占用的内存比别人小,你这代码写的可不就比别人好吗?
这就牵扯到了我们下面要讲的时间&&空间复杂度的概念!
请问兄弟们觉得我们现在是时间优先还是空间优先呢?从前因为技术的限制,内存做的都比较小,这种情况下我们就需要舍弃时间选择空间,但是现在一块内存/硬盘的价格被打下来了,这种情况下,时间就是金钱,其实说到底,只要你足够rich,一切问题都不再是问题了.
时间复杂度
我们可以把时间复杂度理解为程序运行的时间,那么是不是我们就应该记录下这个时间作为时间复杂度的值呢?受到一些客观因素的限制:
1.不同的设备. 2.不同的网速 3.打开不同的程序…
有了这诸多的条件限制,很多时候我们得到的程序运行时间并不具有绝对的参考价值,而且从现实的角度来说,一个程序只要写好了,我们就应该能知道它的时间复杂度,但是如果按照上述的说法,我们必须要时刻把电脑带在身边跑程序才能获得准确的时间复杂度,这显然是不科学的!
因此,我们想到一个程序的执行时间在理论上应该和这个程序执行操作的次数成正比,这个次数不受客观因素影响,只要程序写好了时间复杂度就存在在那里了.所以,我们日后将会使用大O的渐进表示法 来表示时间空间复杂度
大O的渐进表示法
public void test(int N){
int x=0;
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){//第一个循环语句中,x++操作执行了N^2次
x++;
}
}
for(int i=0;i<4N;i++){
x++ //第二个循环语句中,执行了4N次操作
}
int n=4;
while(n!=0){
x++; //第三个循环语句中,执行了4次
n--;
}
}
那么我们用 F(N)=N^2+4N+4 来表示这个方法总的执行次数.
可是如果每次我们都需要这样计算这样表示这样子来比较时间复杂度,那会不会显得很麻烦?
所以我们规定了以下几条:
1. 常数项统统看成1;
2. 只保留最高次项;
3.去除系数项;
其实也不难想:当N很大的时候,其他的那一些花里胡哨的东西不过是跳梁小丑罢了,当执行语句是常数项使,对于计算机来说跟一条其实区别也不是很大,这样子极大程度上优化了我们对于时间复杂度的应用!
通常情况下我们讨论的都会是最差情况下的时间复杂度.
三种时间复杂度
就那寻找有N个元素的数组中某一个值的下标来举例子:
最好情况 :中头奖了,第一个就中了,那时间复杂度就是O(1);
平均情况 :我们遍历数组到一半才找到,时间复杂度(N/2) (仅仅是为了和下面的做出区别)
最坏情况 :倒了霉了,最后才碰到… 这种情况下我们需要遍历完数组:O(N)的时间复杂度!
这边我们主打的就是一个木桶效应,做程序猿可不敢赌,赌我这个程序没有bug,赌我这个时间复杂度很低,这样子是很不科学的一种方法,你要对得起你的工资啊!!
几道例题
一.简单递归
计算递归的时间复杂度:
public int sum(int n){
if(n<=0) return 0;
return sum(n-1)+n;
}
先说好:以后我们在表示时间复杂度的时候习惯性用N来表示问题的规模,N没有特殊的含义,就比如本题中的n就是N.
这里我们乍一看,似乎并没有执行语句啊,难道时间复杂度就是O(1)?
在递归中,我们的时间复杂度=递归次数 * 每个递归中执行语句的次数
在本题中我们的递归语句就是返回的语句,所以时间复杂度就是递归次数,也就是O(N).
public int sum(int n){
if(n<=0) return 0;
for(int i=0;i<N;i++){
sout();
}
return sum(n-1)+n;
}
如果是这样的语句,每次递归中又包含循环之类的,那每个递归的执行语句就不是一了,这个方法目测时间复杂度为O(N)!
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}
之前的递归只有一层还好,那现在我们有两个递归了,我们又应该如何处理呢?
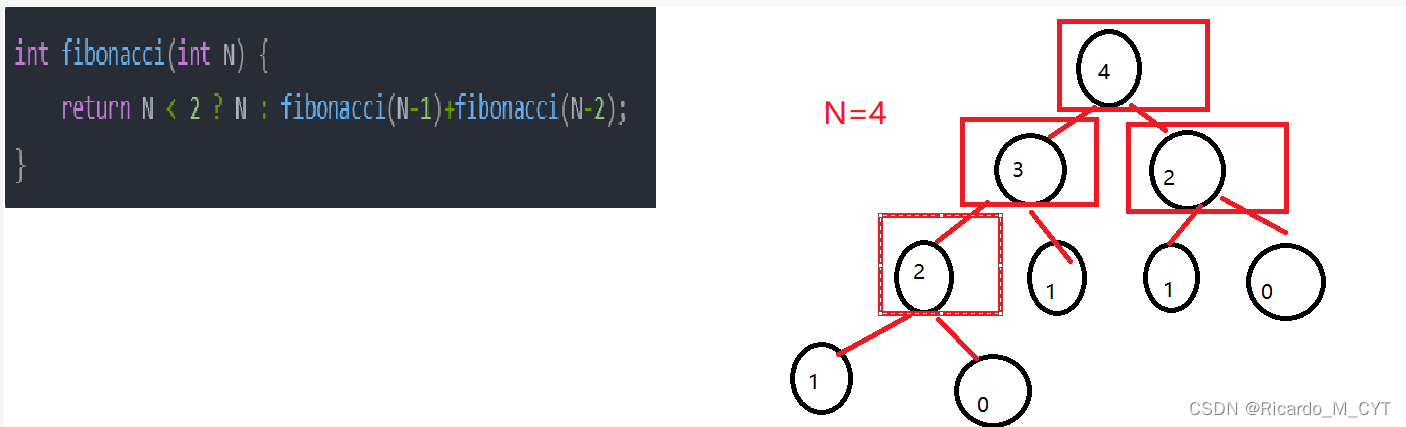
可以看到,我们现在每次递归下来还只是一个三目表达式,而我们需要递归的次数可以近似看成整个树的节点个数,现在我们根据等比数列求和公式可以推导出,时间复杂度是O(2^N),这里我们就发现了,有的时候时间复杂度跟我们想象的可能会有出入.
二结合代码来判断时间复杂度
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1;
}
这是一个很普通的二分查找,按照普通的想法,我们是需要从两端往中间遍历完这个数组的,难道时间复杂度就是O(N)?并不是的,我们要深入代码去看,每一次循环结束,都能够筛掉一半的数据,因此我们从头到尾也只是遍历了一半的一半的一半…的数组长度,所以时间复杂度就应该是O(log N)!
空间复杂度
空间复杂度表示的是一个算法中临时占用存储空间大小的量度,跟时间复杂度一样,这个量度并不是绝对的占用的字节数大小,而是在进行整个算法的时候,我们创建的临时变量的大小.
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1;
}
还拿这个二分查找举例子,虽然看似好像每次循环中我们都会创建一个mid变量,那么我们的空间复杂度是不是就是O(logN)呢?不是的,我们要考虑到一个因素是:在我们第二次进入循环创建变量时,第一次循环中创建的mid变量已经被回收了,等于就是说在整个函数栈帧的同一时刻,我们最多也就是创建了一个变量!
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}
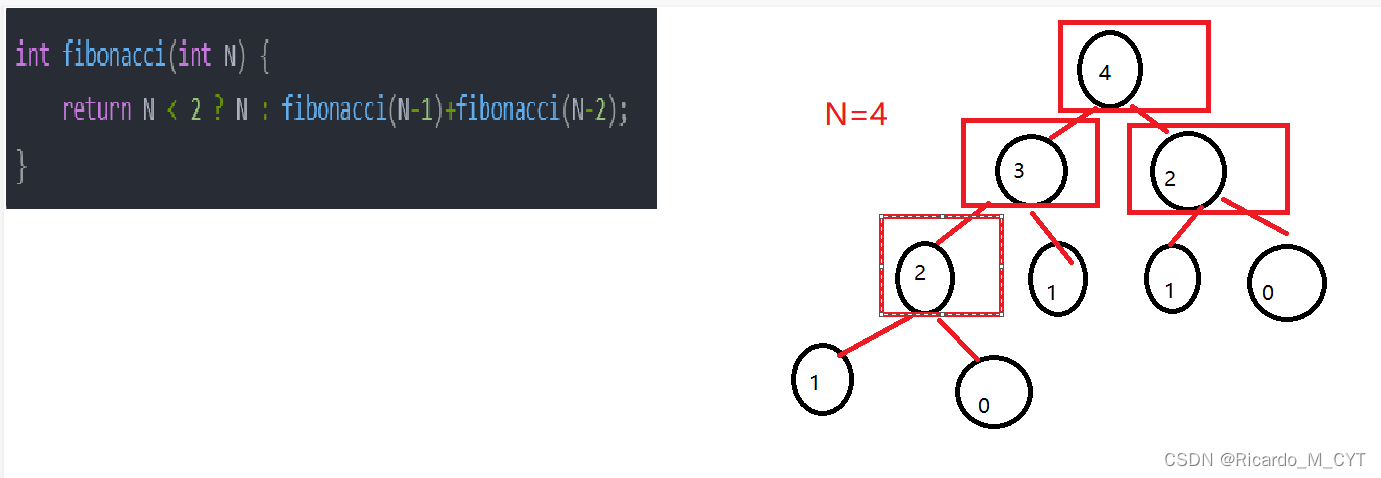
再拿这个斐波那契举例子,虽然看似我们并没有在这个题目中创建变量,但是每一次我们递归下来都会开辟一个栈帧,栈帧也是相当耗费空间的好吧!
而且,对于这个递归来说,我们是一路向左开辟函数栈帧的,当左边的递归语句结束后,我们才会执行右边的,因此,对于整个方法来说,空间复杂度就是O(N)!
希望我的这篇博客能帮助到屏幕前的您!
百年大道,你我共勉!