目录

问题描述：

实现代码与解析：

递归：

原理思路：

迭代：

原理思路：

---

问题描述：

        给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

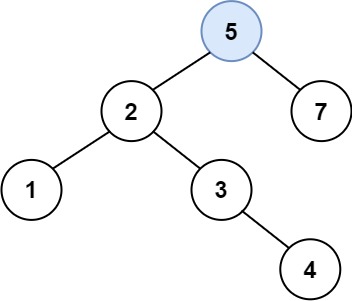
示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

实现代码与解析：

递归：

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) 
    {
        if(root==NULL)
        {
            TreeNode* node=new TreeNode(val);
            return node;
        }
        //大于向右
        if(val>root->val)
        {
            root->right=insertIntoBST(root->right,val);
        }
        //小于向左
        if(val<root->val)
        {
            root->left=insertIntoBST(root->left,val);
        }
        return root;
    }
};

原理思路：

        比较简单，有多种方法，这里我们直接选择在叶子结点插入即可，直接比较结点大小来选择递归方向，不用遍历整个树。

迭代：

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) 
    {
        //根节点为空
        if (root == NULL) 
        {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        TreeNode* cur=root;
        TreeNode* pre= root; // 记录上一个节点
        while (cur != NULL) 
        {
            pre=cur;//更新上一个结点
            if (cur->val > val) cur = cur->left;//向左
            else cur = cur->right;//向右
        }
        TreeNode* node = new TreeNode(val);
        if (val < parent->val) parent->left = node;// 进行连接
        else parent->right = node;
        return root;
    }
};

原理思路：

        与递归同，不过这里要记录上一个结点，来进行结点之间的连接，具体可以看注释。