​​​​​​​​​​​Dashboard - Codeforces Round #842 (Div. 2) - Codeforces

A: 思维+构造

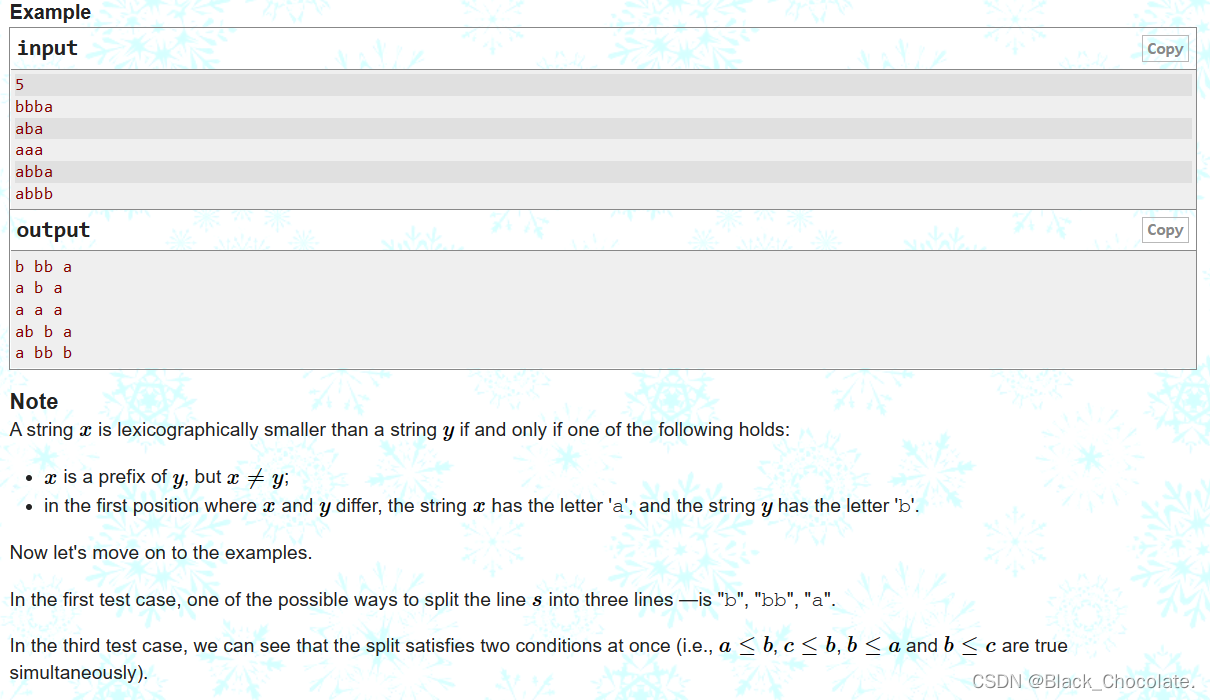
题意：给定一个由 ab 组成的字符串，将该字符串拆分成 3 个部分（a，b，c），要求中间部分的字典序最大或者最小

分析：我们发现，最终的答案是跟b相关的。也就是说，如果我们能够构造字符串b，使其满足条件，那么就可以确定a，c，同时也就可以得到答案。

方法：在除了两端的位置找到一个 a ，如果a存在的话，就可以用这个 a 当作最小字典序的中间段，左右两边的字典序一定大于等于中间单独的 a 。

代码：

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e6+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p

inline void solve(){
	string s;cin>>s;
	if(s[0]!=s[s.size()-1]&&s[1]=='a') cout<<s[0]<<" "<<s[1]<<" "<<s.substr(2,s.size()-2)<<"\n";
	else cout<<s[0]<<" "<<s.substr(1,s.size()-2)<<" "<<s[s.size()-1]<<"\n";
}

signed main(){
	fast;int T;cin>>T;
	while(T--) solve();
}

 B：构造

题意：给定 n 个整数，每个整数给定的形式是某些位上的数是 1 ，求能不能从 c 中获取 2 个子序列，使得两个序列内所有数的 or 值相同。

方法：将两个子序列看作两个集合 a,b 。尽可能的让其中一个子序列包含尽量多的数，令 a 集合为 c 内的所有数。接下来我们只需要找到一个没有用的数并把它踢出去就可以，这样的贪心构造是最优秀的，因为一个数对集合的影响是全局的。如果对于一个数 ci 的所有位，出现的次数都大于 1 ，那么这个数就是可有可无的，因为一定被 a 这个集合包含，那么 b 集合就是除了 ci 这个数以外的所有数的集合。

代码：

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e6+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int n;
vector<int>v[N];
map<int,int>mp;

inline void solve(){
	cin>>n;
	mp.clear();
	for(int i=1;i<=n;i++) v[i].clear();
	bool ok=false;
	for(int i=1;i<=n;i++){
		int m;cin>>m;
		for(int j=1;j<=m;j++){
			int x;cin>>x;
			mp[x]++,v[i].push_back(x);
		}
	}
	for(int i=1;i<=n;i++){
		bool flag=false;
		for(int j=0;j<v[i].size();j++){
			if(mp[v[i][j]]<=1) flag=true;
		}
		if(flag==0) ok=true;
	}
	if(ok==true) cout<<"YES\n";
	else cout<<"NO\n";
}

signed main(){
	int T;cin>>T;
	while(T--) solve();
}

 C:构造

本题解析参考：Codeforces Round #843 (Div. 2) A~E - 知乎

 题意：给定 n,x ，求一个最小的大于等于 n 的数 m ，使得 n&(n+1)&…&m=x 

分析：

 代码：

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e6+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int n;
vector<int>v[N];
map<int,int>mp;

inline void solve(){
	int n,x;cin>>n>>x;
	bitset<64>a(n),b(x);
	int l=n,r=INF;
	for(int i=63;~i;i--){
		if(a[i]==0&&b[i]==1){
			cout<<"-1\n";return;
		}
		if(a[i]==0&&b[i]==0) continue;
		if(a[i]==1&&b[i]==0) l=max(l,((n/(1LL<<i))+1)*(1LL<<i));
		else r=min(r,((n/(1LL<<i))+1)*(1LL<<i)-1);
	}
	if(l<=r) cout<<l<<"\n";
	else cout<<"-1\n";
}

signed main(){
	int T;cin>>T;
	while(T--) solve();
}

E：前缀和

题意：给定一个序列，每次操作先选择一个子序列，然后对奇数位置的数 +1 ，对偶数位置的数 −1 ，求最少操作次数使得所有数变为 0 

方法：前缀和思想：这题我们只需要处理最大的区间即可。为什么？

我们在处理大区间的时候，其余的小区间，可以顺带进行处理。

分析：我们将这个序列转换为前缀和数组，问题最终转变为了：如何使前缀和数组中的每个数变为0所得的最小次数。对于每一次操作，我们可以让任意一些不连续的区间+1 or -1.

那么对于所有的正数，最多需要操作a次，对于所有的负数，最多需要操作-b次（因为负数代表着多余的操作）

那么ans=a-b

代码：

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e6+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int n;
int a[N],sum[N];

inline void solve(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i],sum[i]=sum[i-1]+a[i];
	int a=0,b=0;
	for(int i=1;i<=n;i++){
		a=max(a,sum[i]);
		b=min(b,sum[i]);
	}
	cout<<a-b<<"\n";
}

signed main(){
	int T;cin>>T;
	while(T--) solve();
}