pgvector扩展在IvorySQL Oracle兼容模式下的应用实践

向量数据库是生成式人工智能(GenAI)的关键组成部分。作为PostgreSQL的重要扩展，pgvector支持高达16000维的向量计算能力，使得PostgreSQL能够直接转化为高效的向量数据库。

IvorySQL基于PostgreSQL开发，因此它同样支持添加pgvector扩展。在Oracle兼容模式下，pgvector扩展同样可用，这为习惯使用Oracle的用户使用向量数据库提供了极大的便利。

安装IvorySQL

注意，请确认你的环境已安装了IvorySQL。如尚未安装，可参考安装指南进行配置安装。

https://docs.ivorysql.org/cn/ivorysql-doc/v3.2/v3.2/6

1.1 设置PG_CONFIG环境变量

export PG_CONFIG=/usr/local/ivorysql/ivorysql-3/bin/pg_config

1.2 获取pg_vector源码

git clone --branch v0.6.2 https://github.com/pgvector/pgvector.git

1.3 安装 pgvector

cd pgvector
sudo --preserve-env=PG_CONFIG make
sudo --preserve-env=PG_CONFIG make instal

1.4 psql连接创建扩展

psql -U ivorysql -d ivorysql
ivorysql=# create extension vector;
CREATE EXTENSION

向量相似的对比方法介绍

点积 (dot product)：向量的点积相似度是指两个向量之间的点积值，它适用于许多实际场景，例如图像识别、语义搜索和文档分类等。但点积相似度算法对向量的长度敏感，因此在计算高维向量的相似性时可能会出现问题。

内积 (inner product)：全称为 Inner Product，是一种计算向量之间相似度的度量算法，它计算两个向量之间的点积（内积），所得值越大越与搜索值相似。

欧式距离 (L2)：直接比较两个向量的欧式距离，距离越近越相似。欧几里得距离算法的优点是可以反映向量的绝对距离，适用于需要考虑向量长度的相似性计算。例如推荐系统中，需要根据用户的历史行为来推荐相似的商品，这时就需要考虑用户的历史行为的数量，而不仅仅是用户的历史行为的相似度。

余弦相似度 (Cosine)：两个向量的夹角越小越相似，比较两个向量的余弦值进行比较，夹角越小，余弦值越大。余弦相似度对向量的长度不敏感，只关注向量的方向，因此适用于高维向量的相似性计算。例如语义搜索和文档分类。

pgvector提供的方法

欧式距离 (L2)，内积 (inner product)，余弦相似度 (Cosine)

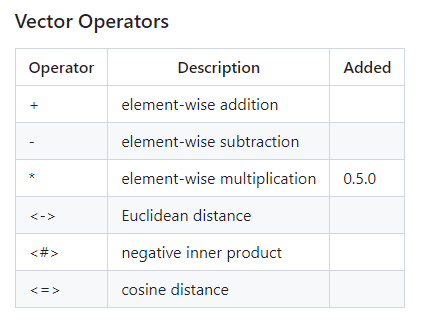
兼容Oracle测试用例，以varchar2作为Oracle兼容字段为例建表：

ivorysql=# CREATE TABLE items (id bigserial PRIMARY KEY, name varchar2(20), embedding vector(3));
CREATE TABLE
ivorysql=# select * from items;
 id |      name      | embedding
----+----------------+-----------
  1 | ora_demo       | [1,2,3]
  2 | ora_compatible | [4,5,6]
(2 rows)

3.1 欧式距离

距离值越小，越相近

ivorysql=# SELECT *, embedding <-> '[3,1,2]' result FROM items ORDER BY embedding <-> '[3,1,2]' LIMIT 5;
 id |      name      | embedding |      result
----+----------------+-----------+-------------------
  1 | ora_demo       | [1,2,3]   | 2.449489742783178
  2 | ora_compatible | [4,5,6]   | 5.744562646538029
(2 rows)

3.2 内积

值越大越与搜索值相似

ivorysql=# SELECT *, embedding <#> '[3,1,2]' result FROM items ORDER BY embedding <#> '[3,1,2]' LIMIT 5;
 id |      name      | embedding | result
----+----------------+-----------+--------
  2 | ora_compatible | [4,5,6]   |    -29
  1 | ora_demo       | [1,2,3]   |    -11
(2 rows)

3.3 余弦相似

两个向量的夹角越小越相似，比较两个向量的余弦值进行比较，夹角越小，余弦值越大。

ivorysql=# SELECT *, embedding <=> '[3,1,2]' result FROM items ORDER BY embedding <=> '[3,1,2]' LIMIT 5;
 id |      name      | embedding |       result
----+----------------+-----------+---------------------
  2 | ora_compatible | [4,5,6]   | 0.11673988938389968
  1 | ora_demo       | [1,2,3]   |  0.2142857142857143
(2 rows)

获取与某向量关联的向量

ivorysql=# SELECT * FROM items WHERE id != 1 ORDER BY embedding <-> (SELECT embedding FROM items WHERE id = 1) LIMIT 5;
 id |      name      | embedding
----+----------------+-----------
  2 | ora_compatible | [4,5,6]
(1 row)

pgvector提供的索引算法

4.1 HNSW

HNSW (Hierarchical Navigating Small World) 是一种基于图的索引算法，它由多层的邻近图组成，因此称为分层的 NSW 方法。它会为一张图按规则建成多层导航图，并让越上层的图越稀疏，结点间的距离越远；越下层的图越稠密，结点间的距离越近。

HNSW 算法是一种经典的空间换时间的算法，它的搜索质量和搜索速度都比较高，但是它的内存开销也比较大，因为不仅需要将所有的向量都存储在内存中。还需要维护一个图的结构，也同样需要存储。所以这类算法需要根据实际的场景来选择。

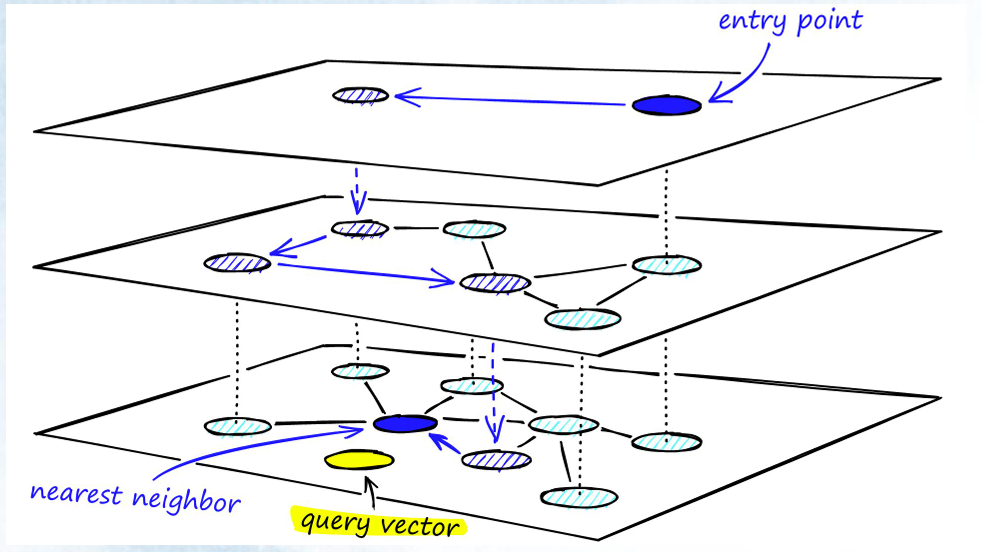
pgvector的HNSW索引算法与Oracle兼容类型没有任何冲突，所以无需关心Oracle兼容类型是否会影响索引创建。

（1） L2 distance HNSW index

ivorysql=# CREATE INDEX ON items USING hnsw (embedding vector_l2_ops);
CREATE INDEX

（2）Inner product HNSW index

ivorysql=# CREATE INDEX ON items USING hnsw (embedding vector_ip_ops);
CREATE INDEX

（3） Cosine distance HNSW index

ivorysql=# CREATE INDEX ON items USING hnsw (embedding vector_cosine_ops);
CREATE INDEX

4.2 ivfflat

它的工作原理是将相似的向量聚类为区域，并建立一个倒排索引，将每个区域映射到其向量。这使得查询可以集中在数据的一个子集上，从而实现快速搜索。

通过调整列表和探针参数，ivfflat 可以平衡数据集的速度和准确性，使 PostgreSQL 有能力对复杂数据进行快速的语义相似性搜索。

通过简单的查询，应用程序可以在数百万个高维向量中找到与查询向量最近的邻居。对于自然语言处理、信息检索等，ivfflat 是一个比较好的解决方案

在建立 ivfflat 索引时，你需要决定索引中包含多少个 list。每个 list 代表一个 "中心"；这些中心通过 k-means 算法计算而来。一旦确定了所有中心，ivfflat 就会确定每个向量最靠近哪个中心，并将其添加到索引中。

当需要查询向量数据时，你可以决定要检查多少个中心，这由 ivfflat.probes 参数决定。这就是 ANN 性能/召回率的结果：访问的中心越多，结果就越精确，但这是以牺牲性能为代价的。

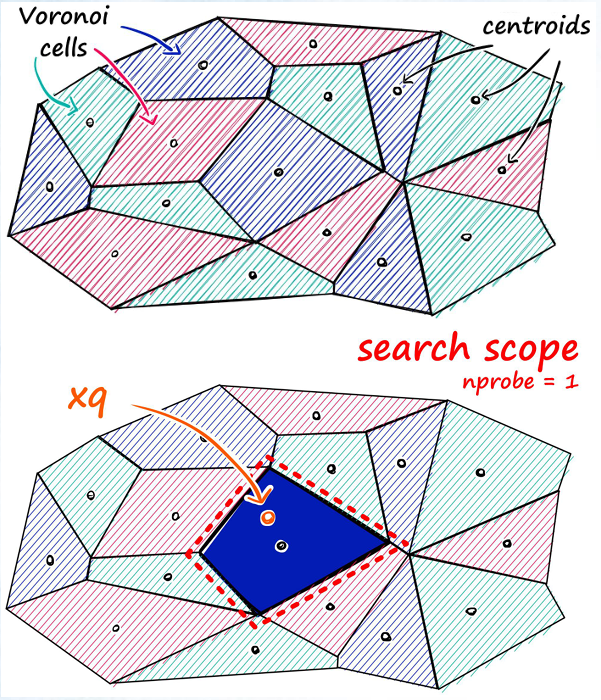
pgvector的ivfflat 索引算法与Oracle兼容类型没有任何冲突，所以无需关心Oracle兼容类型是否会影响索引创建。

（1）L2 distance ivfflat index

ivorysql=# CREATE INDEX ON items USING ivfflat (embedding vector_l2_ops);
CREATE INDEX

（2） Inner product ivfflat index

ivorysql=# CREATE INDEX ON items USING ivfflat (embedding vector_ip_ops);
CREATE INDEX

（3） Cosine distance ivfflat index

ivorysql=# CREATE INDEX ON items USING ivfflat (embedding vector_cosine_ops);
CREATE INDEX

其他类型

5.1 Binary Vectors

Use thebit type to store binary vectors

ivorysql=# CREATE TABLE items5 (id bigserial PRIMARY KEY, name varchar2(20), num number(20), embedding bit(3));
CREATE TABLE
ivorysql=# INSERT INTO items5 (name, num, embedding) VALUES ('1st oracle data',0, '000'), ('2nd oracle data', 111, '111');
INSERT 0 2
ivorysql=# SELECT * FROM items5 ORDER BY bit_count(embedding # '101') LIMIT 5;
 id |      name       | num | embedding
----+-----------------+-----+-----------
  2 | 2nd oracle data | 111 | 111
  1 | 1st oracle data | 0   | 000
(2 rows)

Oracle兼容特性与pgvector适配

IvorySQL不仅支持Oracle的数据类型，还能够适配Oracle的匿名块、存储过程和函数等特性。安装了pgvector扩展的IvorySQL同样具备上述功能

6.1 匿名块

ivorysql=# declare
i vector(3) := '[1,2,3]';
begin
raise notice '%', i;
end;
ivorysql-# /
NOTICE:  [1,2,3]
DO

6.2 存储过程

ivorysql=# CREATE OR REPLACE PROCEDURE ora_procedure()
AS
p vector(3) := '[4,5,6]';
begin
raise notice '%', p;
end;
/
CREATE PROCEDURE
ivorysql=# call ora_procedure();
NOTICE:  [4,5,6]
CALL

6.3 函数

ivorysql=# CREATE OR REPLACE FUNCTION AddVector(a vector(3), b vector(3))
RETURN vector(3)
IS
BEGIN
RETURN a + b;
END;
/
CREATE FUNCTION
ivorysql=# SELECT AddVector('[1,2,3]','[4,5,6]') FROM DUAL;
 addvector
----------------
 [5,7,9]
(1 row)

*参考文章

《向量数据库与pgvector》

https://zhuanlan.zhihu.com/p/649779973