0. 预备知识

快速傅里叶变换旨在解决离散傅里叶变换DFT计算量大效率低的问题。当我们想要抑制噪声提取出某段信号中的有效信息时，如系统模型辨识或者是使用高精度力传感器测量人体腕部寸关尺脉搏信号这类应用，应该如何设计采样流程？

首先，应当考虑采样频率 $f_s$ 的问题，根据香农采样定理，采样频率应大于等于目标信号频率 $f$ 最高频段的2倍，工程中通常取2.56到4倍的频率。采样频率可以直接配置传感器的采样触发信号，对于采样频率固定的设备，如普通家用摄像头，则需要根据应用选择设备型号。采样频率最好是2的幂次。
其次，采样时间的问题，在确定采样频率后等同于确定采样点数量 $N$ 。采样点数量越多，则FFT变换后生成的频谱的频段间隔越小，即分辨力越高。采样数据点数量最好是采样频率的倍数关系。

FFT应用时需要主意的点包括：

FFT输出的频谱是双边对称的，关于第 $N /2$ 个数据点左右对称，每一个数据点是一个复数 $a+b\mathbf{j}$ ，这些数据点只有幅值和相位是具有实际意义的。
FFT输入 $N$ 个数据点，输出 $N$ 个频段的复数，可以通过这些复数计算出对应的相位和未归一化的幅值。对幅值部分进行归一化时需要主意的是，直流分量需要除以 $N$ ，剩余分量需要除以 $N /2$ 。
由于FFT是双边对称的，因此频率和幅值部分应该取前半段，频段点为： $f=(n-1)f_s/N$ ，需要注意，因为FFT输出的结果是双边的，只有前半段的频谱是有意义的，因此这里 $n$ 的取值范围是 $n = 1, ..., N /2$

当我们理解fft的过程，就可以调整不同频段的幅值，重新组合出一个过滤后的信号。

1. 代码示例

1.1 代码

借用这位老哥的案例： https://blog.csdn.net/qq_27825451/article/details/88553441?spm=1001.2014.3001.5506 。
我们重新写一份FFT的代码，分析信号的频谱：

'''
Author: Dianye Huang
Date: 2023-01-14 10:26:47
LastEditors: Dianye Huang
LastEditTime: 2023-01-14 14:37:02
Description: 
'''

import numpy as np
from scipy.fftpack import fft, ifft
import matplotlib.pyplot as plt

class myFFT:
    def __init__(self):
        pass
    
    def get_spetrum(self, data, fs, flag_plt=False):
        N = len(data)
        fft_y = fft(data)        # get complex number
        abs_y = np.abs(fft_y)    # get magnitude
        ang_y = np.angle(fft_y)  # get phase
        nrm_y = abs_y/(N/2)      # get normailzed magnitude (A0/N, A1.../(N/2))
        nrm_y[0] = nrm_y[0]/2      
        nmh_y = nrm_y[:int(N/2)] # half normalized magnitude
        agh_y = ang_y[:int(N/2)] # half normalized angle
        spes  = np.arange(int(N/2))*fs/N  # specturm axis 
        
        if flag_plt:
            plt.figure()
            x = np.arange(N)
            plt.subplot(2,3,1)
            plt.plot(x/fs, data)
            plt.title('raw signal')
            plt.xlabel('Time (s)')
            
            plt.subplot(2,3,4)
            plt.plot(x[:50]/fs, data[:50])
            plt.title('partial raw signal')
            plt.xlabel('Time (s)')
            
            plt.subplot(2,3,2)
            plt.plot(x, abs_y)
            plt.title('magnitudes')
            plt.xlabel('Sample index')
            
            plt.subplot(2,3,5)
            plt.plot(x, ang_y)
            plt.title('angles')
            plt.xlabel('Sample index')
            
            plt.subplot(2,3,3)
            plt.plot(x, nrm_y)
            plt.title('nomalized magnitude')
            plt.xlabel('Sample index')
            
            plt.subplot(2,3,6)
            plt.plot(spes, nmh_y)
            plt.title('half nomalized magnitude')
            plt.xlabel('Frequency (Hz)')
            
            plt.show()
        
        return nmh_y, agh_y, spes

    def get_fft(self, data, fs):
        N = len(data)
        fft_y = fft(data)
        tmp_arr = np.arange(0, fs/2, fs/N)
        freq_y = np.hstack((tmp_arr, np.flip(tmp_arr, axis=0)))
        return fft_y, freq_y
    
    def create_demo_signal(self, N=2800, fs=1400):
        # create a signal along with sample rate
        t = np.arange(0, N/fs, 1/fs)
        y = 3 + 7*np.sin(2*np.pi*200*t) + 5*np.sin(2*np.pi*400*t) + 3*np.sin(2*np.pi*600*t)
        noise_arr = np.random.normal(0, 2, N)
        return t, y+noise_arr, fs
    
if __name__ == '__main__':
    mfft=myFFT()
    t, data, fs = mfft.create_demo_signal(N=4096, fs=2048)
    # mags, angs, spes = mfft.get_spetrum(data, fs, flag_plt=True) 
    fft_y, freq_y = mfft.get_fft(data, fs)
    fft_y[freq_y>450] = 0
    sig = ifft(fft_y)
    
    plt.figure()
    plt.plot(t[:50], data[:50])
    plt.plot(t[:50], sig[:50])
    plt.show()

1.2 总结

$ff t$ 和 $i ff t$ 的求解包在scipy.fftpack中
复数的幅值和相位可以使用numpy包中的np.abs()和np.angle()函数

示例程序运行结果如下：

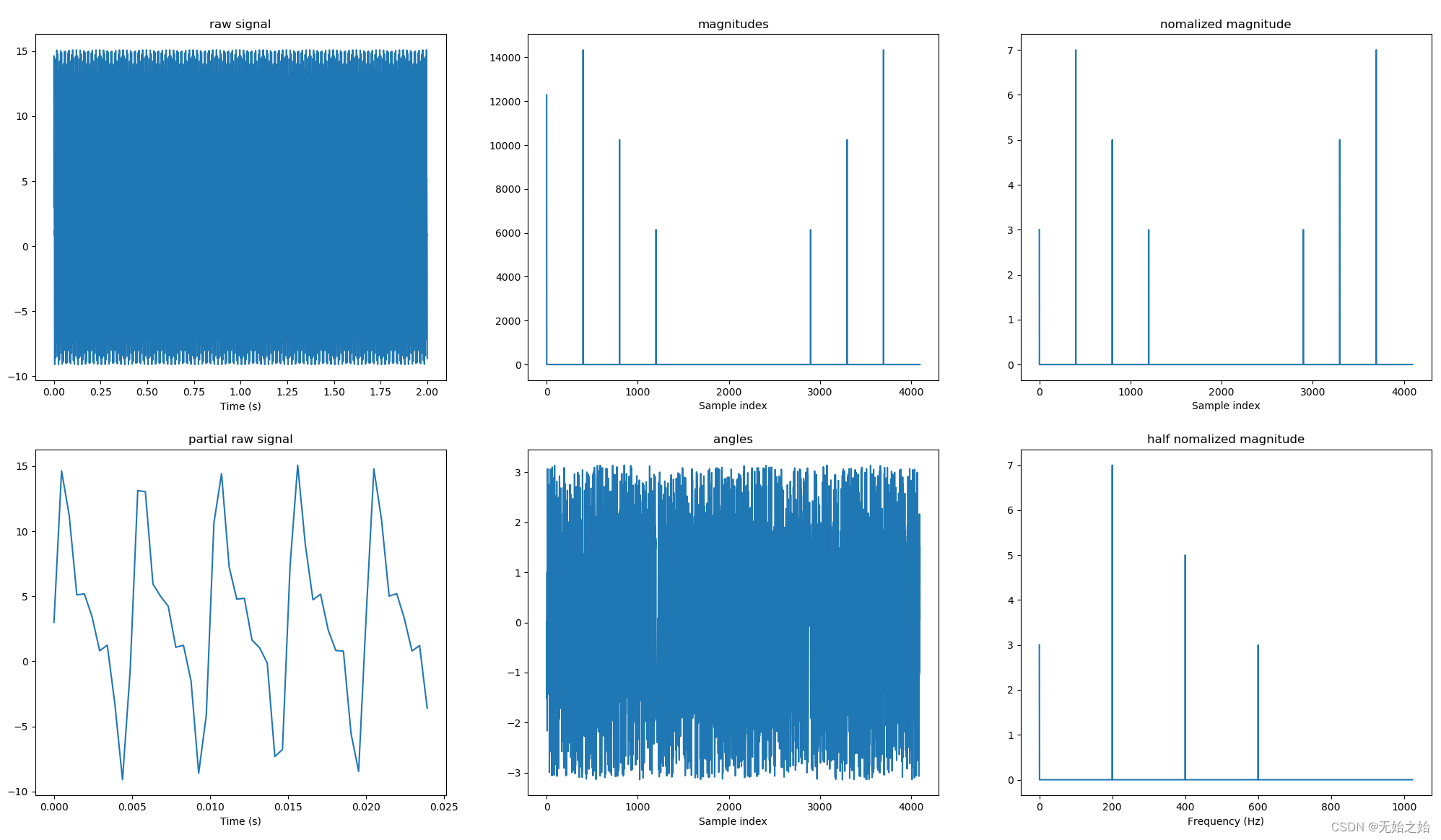
1.2.1 分析频谱，右下角为最终结果

if __name__ == '__main__':
    mfft=myFFT()
    t, data, fs = mfft.create_demo_signal(N=4096, fs=2048)
    mags, angs, spes = mfft.get_spetrum(data, fs, flag_plt=True)

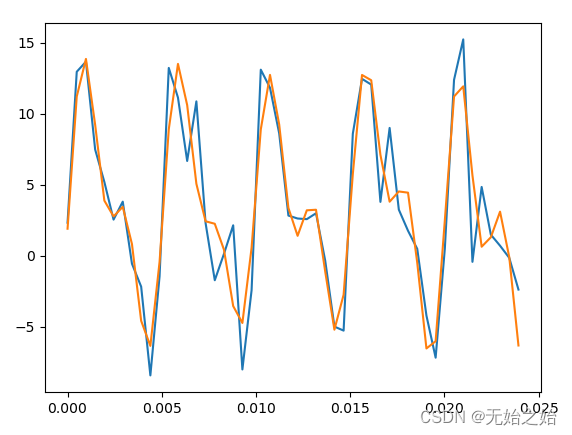
在这里插入图片描述

1.2.2 简单的滤波，除去大于450Hz的分量利用ifft重新组合信号的结果

if __name__ == '__main__':
    mfft=myFFT()
    t, data, fs = mfft.create_demo_signal(N=4096, fs=2048)
    
    fft_y, freq_y = mfft.get_fft(data, fs)
    fft_y[freq_y>450] = 0
    sig = ifft(fft_y)
    
    plt.figure()
    plt.plot(t[:50], data[:50])
    plt.plot(t[:50], sig[:50])
    plt.show()