前言

卷积运算实际上是一种常见的数学方法，与加法，乘法等运算类似，都是由两个输入的到一个输出。不同的是，卷积运算输入的是两个信号，输出第三个信号。除了信号处理外，卷积运算也常用于概率论与数理统计等其他诸多领域。在线性系统中，卷积用于描述信号（Input Signal）,冲激响应(Impulse Response),以及输出信号（Output Signal）3者之间的关系。

数字信号处理与卷积运算

卷积运算符号一般用*来表示，故表达式为：
y[n]=x[n]*h[n]
x[n]为输入信号，h[n]为冲激响应，y[n]为输出信号。卷积的常见用途是信号滤波。
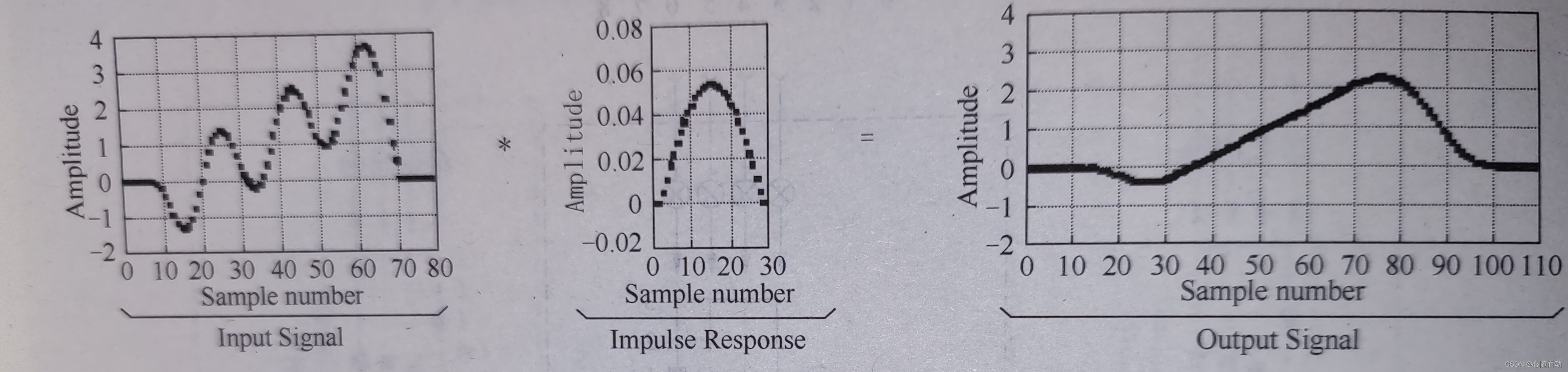
在这里插入图片描述
（a）低通滤波器

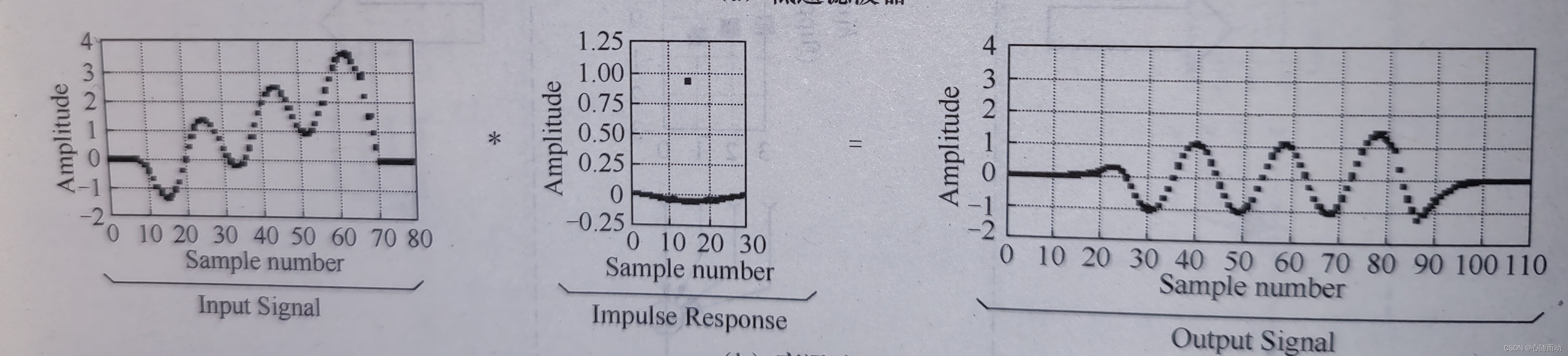
(b)高通滤波器
在数字信号处理的各种应用中，输入信号的长度可能会有成百上千乃至数百万个采样点。冲激响应信号的长度通常要短得多，例如，只有几个或几百个采样点。虽然卷积运算并不限制这些信号的长度，然而，我们仍然需要搞清楚信号长度。
假设输入信号x[n]的长度为N（采样点的下标为0——N——1），冲激响应信号h[n]的长度为M（采样点的下标设为0——M-1），则输出信号y[n]长度为N+M-1

卷积公式与计算过程

卷积计算示意图
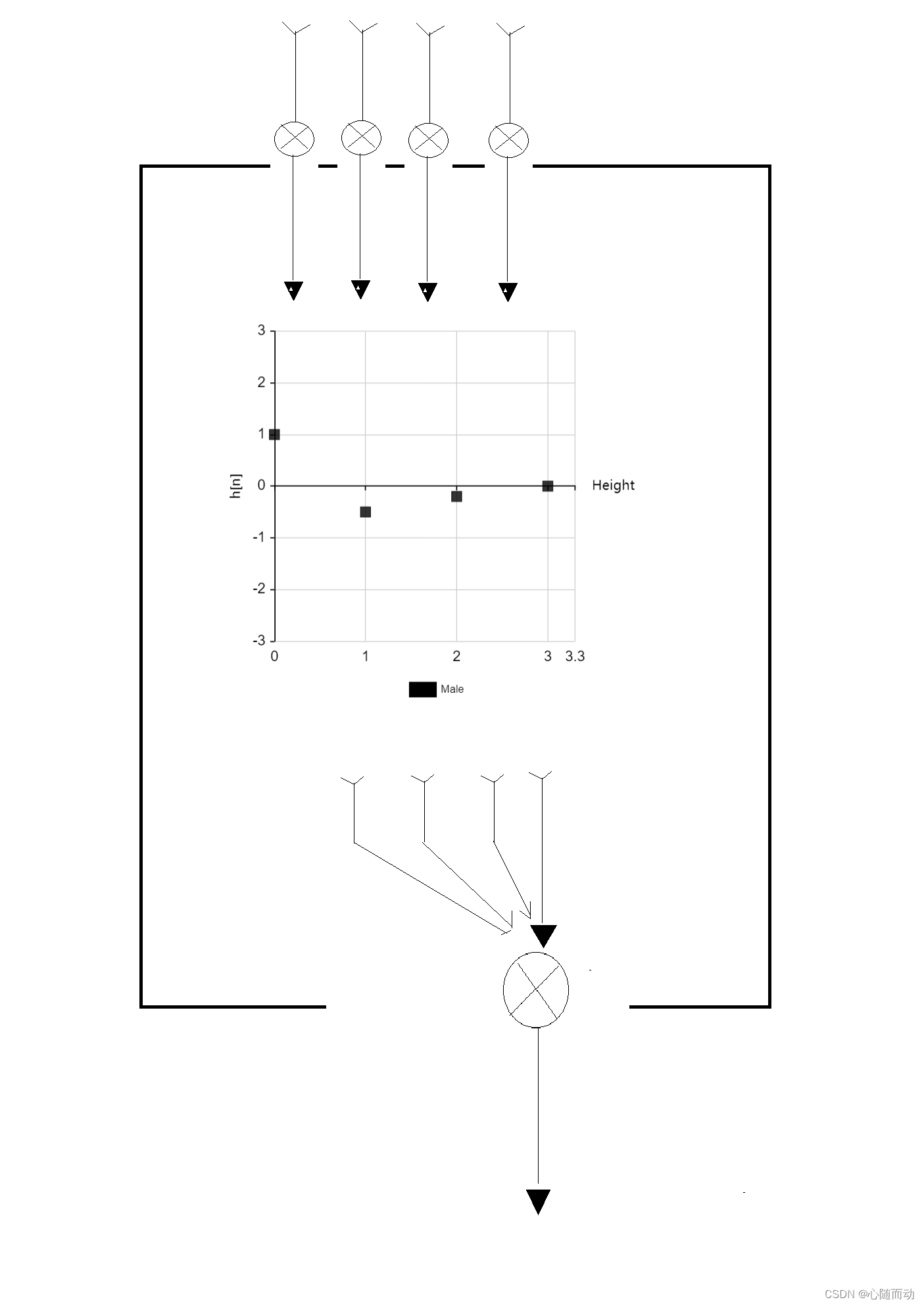
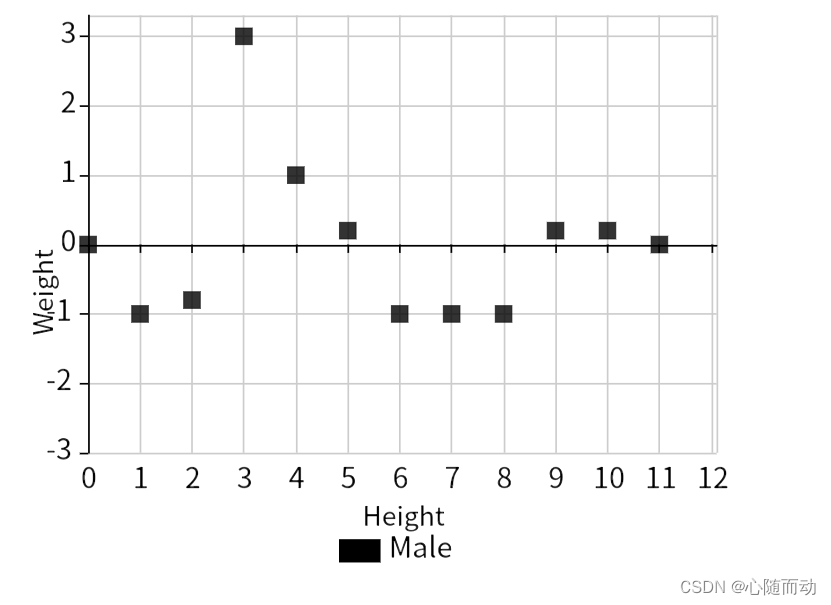
在这里插入图片描述

边缘卷积计算与0填充

当我们计算y0或y11等信号边缘处点的卷积时，会发现有些问题。例如，计算y0时，则将h0与x0对齐，此时我们会发现，h3,h2,h1的对应采样点应为x(-1),x(-2),x(-3),而这些点却根本不存在。类似的，当计算y11时，我们也会面对不存在的x9,x10,x11。
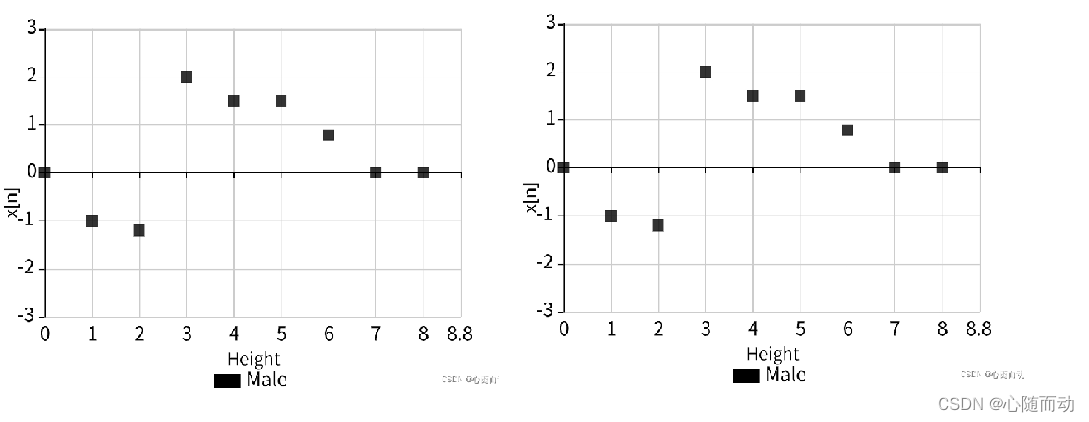
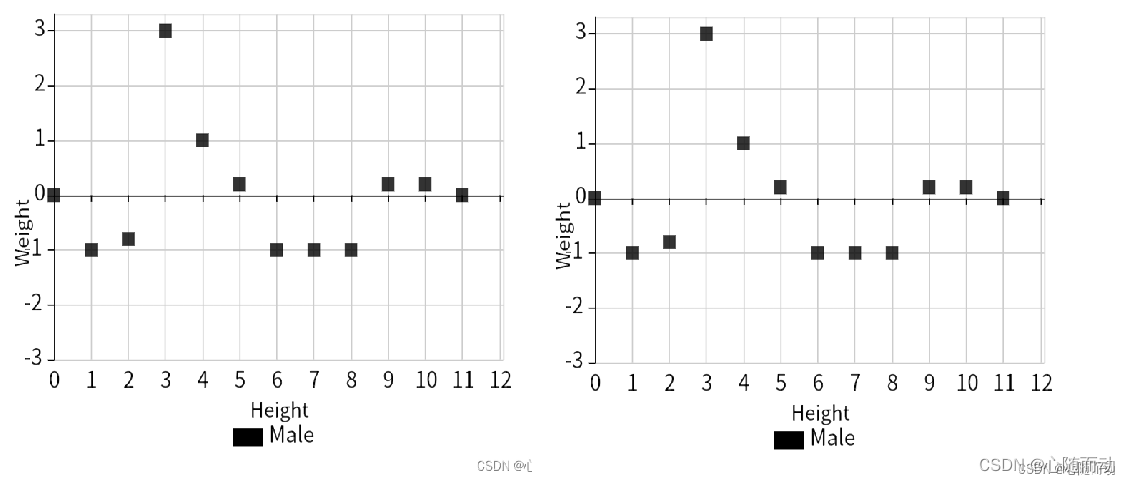
在这里插入图片描述

在这里插入图片描述
对于以上所描述的卷积计算过程，我们可以通过下列代码实现：

import numpy as np
def MyConvolve(input,kernel):
    #对h[n]进行180度翻转
    kernel_flipped=np.array([kernel[len(kernel)-1-i] for i in range(len(kernel))])
    #kernel_flipped=kernel[::-1]也可以翻转
    len_input=len(input) #x[n]的长度
    len_kernel=len(kernel) #h[n]的长度


    #对输入数组进行0填充来解决卷积计算过程中的边缘对齐
    padding=np.zeros(len_kernel-1,dtype='int') #填充数值为0
    temp_pad=np.append(padding,input)
    input_pad=np.append(temp_pad,padding) #0填充后的数据

    #定义一个数组保存卷积结果，数组长度为：x[n]的长度+h[n]的长度-1
    con_array=np.array(range(len_input+len_kernel-1))

    #对x[n]与h[n]进行卷积计算
    for m in range(len(con_array)):
        sum_con=0
        for n in range(len(kernel_flipped)):
            sum_con=sum_con+input_pad[n+m]*kernel_flipped[n]
        con_array[m]=sum_con
    
    #输出卷积结果
    print('Input Signal:',input)
    print("Convolution Kernel:",kernel)
    print('Convolution:',con_array)
if __name__=='__main__':
    input=[1,3,5,7,9,11,13]
    kernel=[2,3,6,8]
    MyConvolve(input,kernel)

结果展示：

Input Signal: [1, 3, 5, 7, 9, 11, 13]
Convolution Kernel: [2, 3, 6, 8]
Convolution: [  2   9  25  55  93 131 169 177 166 104]

NumPy卷积函数

NumPy模块也内置了卷积函数，函数原型为：numpy.convolve(a,v,mode='full).
a`:输入一维数组，长度为N.
v:输入的第二个一位数组，长度为M。
mode:有三个参数（full，valid，same）
full,默认值。计算每一个采样点的卷积值，返回的数组长度为N+M-1.在卷积的边缘处，此信号不重叠，存在边缘效应
valid,返回的数组长度为max(M,N)-min(M,N)+1.此时返回的是完全重叠的点，边缘点无效，因此无边缘效应
same,返回的数组长度为max(M,N),边缘效应依然存在
NumPy卷积函数示例代码：


import numpy as np
a=[1,3,5,7,9,11,13]
b=[2,4,6,8]
c1=np.convolve(a,b,mode='full')
print("full卷积计算",c1)
c2=np.convolve(a,b,mode='same')
print('same计算',c2)
c3=np.convolve(a,b,mode='valid')
print('valid计算',c3)

计算结果：

>>> import numpy as np
>>> a=[1,3,5,7,9,11,13]
>>> b=[2,4,6,8]
>>> c1=np.convolve(a,b,mode='full')
>>> print("full卷积计算",c1)
full卷积计算 [  2  10  28  60 100 140 180 190 166 104]
>>> c2=np.convolve(a,b,mode='same')
>>> print('same计算',c2)
same计算 [ 10  28  60 100 140 180 190]
>>> c3=np.convolve(a,b,mode='valid')
>>> print('valid计算',c3)
valid计算 [ 60 100 140 180]
>>>

二维矩阵卷积计算

在进行数字图像处理时，每幅图像对应的是二维离散信号。我们经常会将一些具有某种特征的二维数组作为模板与图像进行卷积操作。使得新的图像具有某种特征，诸如模糊，锐化，浮雕等，这些模板统称为卷积核（Convolution Kernel）.图像与卷积核之间的卷积操作从原理上与上文所述的一维信号卷积计算过程基本类似：将卷积核视为一个m*n大小的窗口一次在图像上滑动，将图像每个像素点上的灰度值与对应的卷积核上的数值相乘，然后将所有相乘后的值累加作为卷积核中间像素对应像素的灰度值，以此类推，计算所有像素点的卷积值。
例如，如图：
（0*4）+（0*0）+（0*0）+(0*0)+(1*0)+(1*0)+(0*0)+(1*0)+(2*-4)=-8
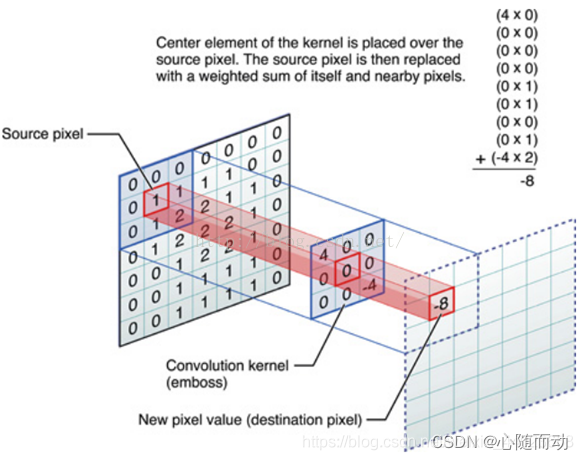在这里插入图片描述图像卷积时一般不进行边缘填充，因此，卷积操作可能导致图像变小（损失图像边缘）。在进行卷积操作计算之前，卷积核也需要180°翻转。例如，卷积核为[[1,2,3],[4,5,6],[7,8,9]],反转后则为[[9,8,7],[6,5,4],[3,2,1]].二维数组的180°翻转可通过数组切片（Slice）与重塑（Reshape）操作来完成。示例代码如下：

import numpy as np
def ArrayRotate180(matrix):
    new_arr=matrix.reshape(matrix.size)  #将二维数组重塑为一维数组
    new_arr=new_arr[::-1] #一维数组实现翻转
    new_arr=new_arr.reshape(matrix.shape) #将一维数组重塑为二维数组
    return new_arr
if __name__=='__main__':
    m=np.array([[1,2,3],[4,5,6],[7,8,9]])
    print(ArrayRotate180(m))

结果展示：
[[9 8 7]
 [6 5 4]
 [3 2 1]]

二维数组卷积计算涉及矩阵运算和矩阵求和，卷积计算的步骤：
①.先将卷积核翻转180°
②.将翻转后的卷积核中心与输入二维矩阵数组第一个元素对齐，并将相乘后得到的矩阵所有元素进行求和，得到结果矩阵的第一个元素。如果考虑边缘效应，那么卷积核与输入矩阵不重叠部分用0填充
③.依此类推，完成其他所有元素的卷积运算，直至输出结果矩阵
完成上述过程代码示例：

import numpy as np
def ArrayRotate180(matrix):
    new_arr=matrix.reshape(matrix.size)  #将二维数组重塑为一维数组
    new_arr=new_arr[::-1] #一维数组实现翻转
    new_arr=new_arr.reshape(matrix.shape) #将一维数组重塑为二维数组
    return new_arr

def My2Dconv(matrix,kernel):
    #对矩阵数组进行深复制作为输出矩阵，而输出矩阵将改变其中参与卷积计算的元素。
    new_martix=matrix.copy()
    m,n=new_martix.shape #输入二维矩阵的行列数
    p,q=kernel.shape #卷积核的行列数
    kernel=ArrayRotate180(kernel) #对卷积核进行180杜翻转;
    #将卷积核与输入二维矩阵进行卷积计算
    for i in range(1,m):
        for j in range(1,n-1):
            new_martix[i,j]=(matrix[(i-1):(p-1+i),(j-1):(j+q-1)]*kernel).sum()
    return new_martix
if __name__=='__main__':
    input=np.array([[1,2,3,4],[5,7,8,8],[6,9,0,2],[11,22,33,44]])
    kernel=np.array([[1,0,1],[-1,-1,-1]]) #示例卷积核
    print(My2Dconv(input,kernel))

结果展示:

[[  1   2   3   4]
 [  5   7   6   8]
 [  6 -14 -12   2]
 [ 11  29  55  44]]

图像卷积应用实例

对于二维矩阵卷积计算，诸如SciPy,OpenCV等等第三方Python模块同样也内置了该功能，以下示例代码利用OpenCV内置的filter2D（）对一幅输入图像进行边缘检测。卷积核在很大程度上决定了输出图像的效果。例如，[[-1,-1,-1],[-1,8,-1],[-1,-1,-1]]可实现对一幅图像进行边缘化检测，[[-1,-1,-1],[-1,9,-1],[-1,-1,-1]]可实现对图像进行锐化操作.[[-6,-3,0],[-3,1,-3],[0,3,6]]可实现对图像进行浮雕处理。
下面展示对图像锐化处理:

#图像卷积应用示例
import matplotlib.pyplot as plt
import pylab
import cv2
import numpy as np
img=plt.imread('D:\csdn专用图片\cb967cce-56cd-45de-ba96-ffb05edabd8b_batchwm.jpg')
plt.imshow(img)
pylab.show()
#定义卷积核
kernel=np.array([[-1,-1,-1],[-1,8,-1],[-1,-1,-1]])
res=cv2.filter2D(img,-1,kernel)
plt.imshow(res)
plt.imsave('result.jpg',res)
pylab.show()