台阶问题

题目描述

有$N$级的台阶，你一开始在底部，每次可以向上迈最多$K$级台阶（最少$1$级），问到达第$N$级台阶有多少种不同方式。

输入格式

两个正整数N，K。

输出格式

一个正整数，为不同方式数，由于答案可能很大，你需要输出$ans\mathrm{mod}100003$后的结果。

样例 #1

样例输入 #1

5 2

样例输出 #1

8

提示

对于$20\%$的数据,有$N\le 10,K\le 3$;

对于$40\%$的数据，有$N\le 1000$;

对于$100\%$的数据，有$N\le 100000,K\le 100$。

---

列举一下事例
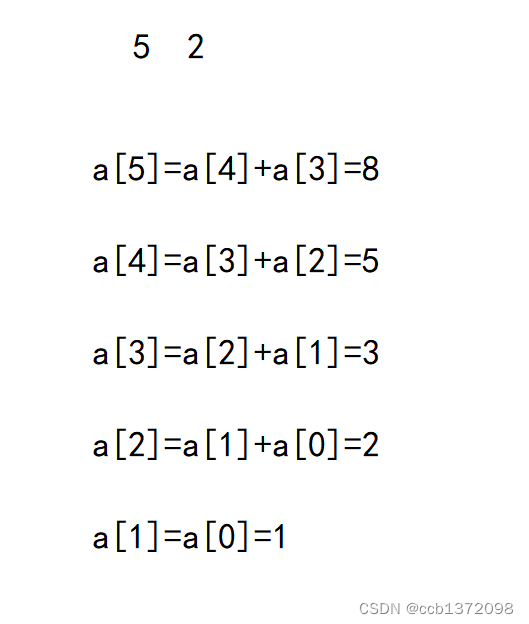就会发现规律，至多一次性爬k阶，那么第n阶就是由n-k,n-k-1,n-k-2…1的情况上来，把以上情况全部加起来，就是n阶的总方法。

#include<bits/stdc++.h>

using namespace std;

int n,k;

int a[200000];
int main()
{

	cin>>n>>k;

	a[0]=1;
	
	for(int i=1;i<=n;++i){
		
		for(int j=1;i-j>=0&&j<=k;++j){
			
			a[i]+=a[i-j];
			
			a[i]=a[i]%100003;
			
		}
		
//		cout<<i<<":"<<a[i]<<endl;
	}
	
	cout<<a[n]<<endl;

	return 0;
}