A V L树

news2024/11/20 12:32:30

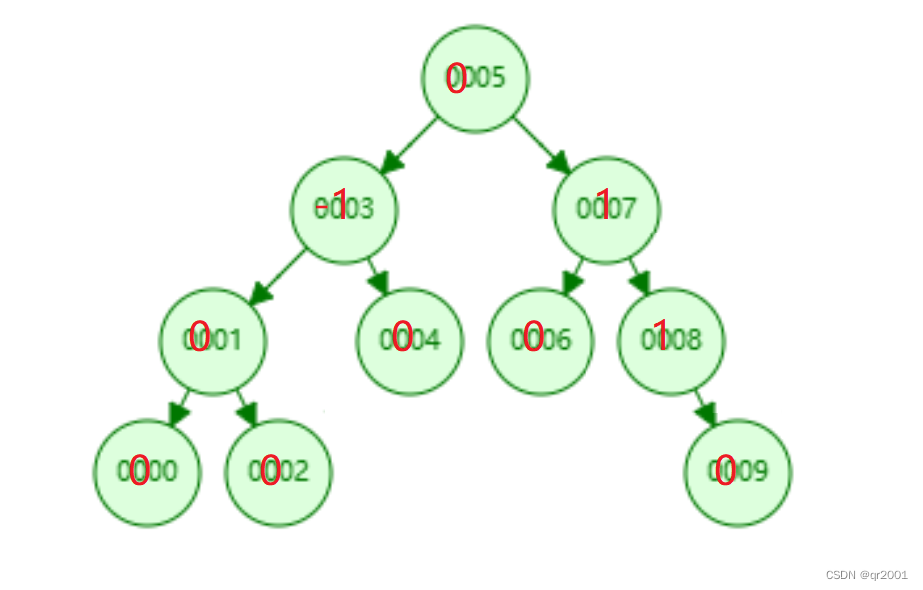
概念

在之前介绍了搜索二叉树，但是当我们插入的数据若是有序或者接近于有序，那么此时查找的效率底下，于是俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，是二叉树更加平衡，从而减少平均搜索长度。

AVL树的性质

  1. 它的左右子树都是AVL树
  2. 左右子树的高度之差的绝对值不超过1(-1/0/1)(高度之差简称为平衡因
    在这里插入图片描述

AVL树实现

在AVL树的实现这里我们只来实现一下它的插入，我们采用记录平衡因子的方式来定义完成AVL树的实现。
我们先来定义它的节点

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	int _bf;//平衡因子  balance factor

	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
};

这里的_bf我们当作这个节点的平衡因子，我们默认这里的平衡因子为右子树的高度减去左子树的高度。
在我们插入之前，我们首先要遵循搜索树的规则，找到空的位置

bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(KV);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;

		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			cur->_parent = parent;
			parent->_right = cur;
		}
		else
		{
			cur->_parent = parent;
			parent->_left = cur;
		}
	}

在找到位置之后我们需要去更新平衡因子，这里有五种情况

  1. 插入的cur的位置为parent的右边的时，此时右子树的高度加一，那么parent->_bt++;
  2. 插入的cur的位置为parent的左边的时，此时右子树的高度加一，那么parent->_bt–;
  3. 更新以后，parent的平衡因子要是是0，那么更新结束，因为插入一个节点之后这个节点的_bf变为了0，代表这个新增的节点一定是插入在高度小的那边的，因此parent的所在的子树高度不变。
  4. 更新以后，parent的平衡因子要是是1或者-1，那么继续向上更新，因为插入一个节点前parent->_bf就是0，那么parent的高度变化了，因此parent的父亲的平衡因子也肯定要变化。
  5. 更新之后，parent->_bt==-2/2,parent已经不平衡了，需要进行旋转处理

旋转

右单旋

新节点插入较高左子树的左侧—左左
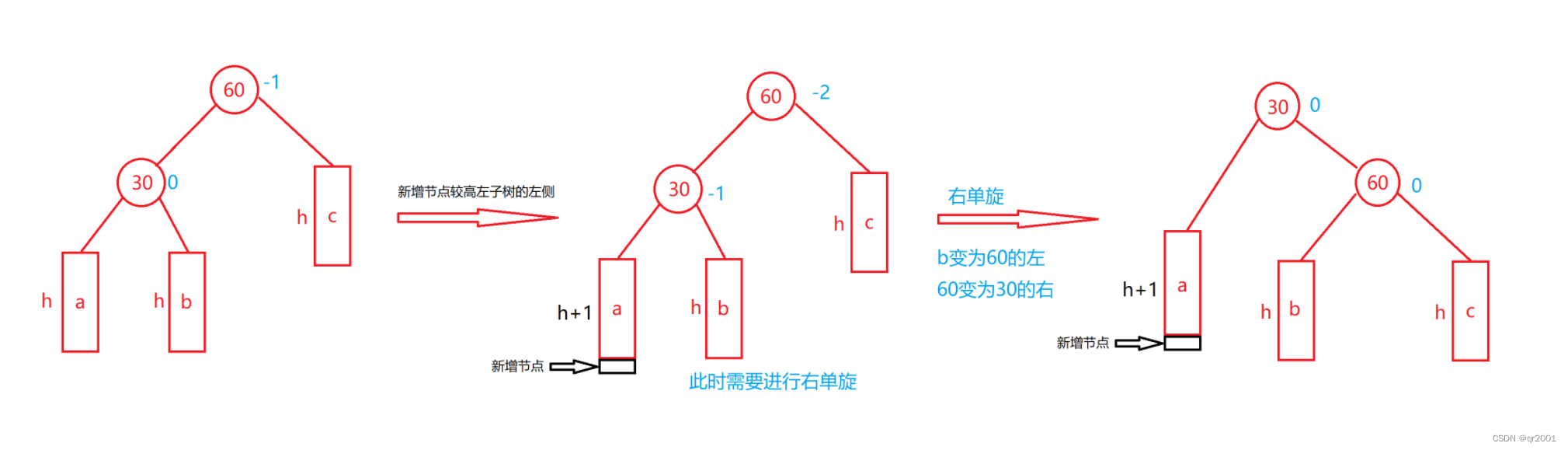
在这里插入图片描述
代码实现

void RotateR(Node* parent)
	{
		Node* SubL = parent->_left;
		Node* SubLR = SubL->_right;

		parent->_left = SubLR;
		//此时SubLR可能为空
		if (SubLR)
		{
			SubLR->_parent = parent;
		}

		Node* parentparent = parent->_parent;

		SubL->_right = parent;
		parent->_parent = SubL;

		if (parent == _root)
		{
			_root = SubL;
			SubL->_parent = nullptr;
		}
		else
		{
			if (parent == parentparent->_left)
			{
				parentparent->_left = SubL;
				SubL->_parent = parentparent;
			}
			else
			{
				parentparent->_right = SubL;
				SubL->_parent = parentparent;
			}
		}
		parent->_bf = SubL->_bf = 0;
	}

左单旋

新节点插入较高右子树的右侧—右右
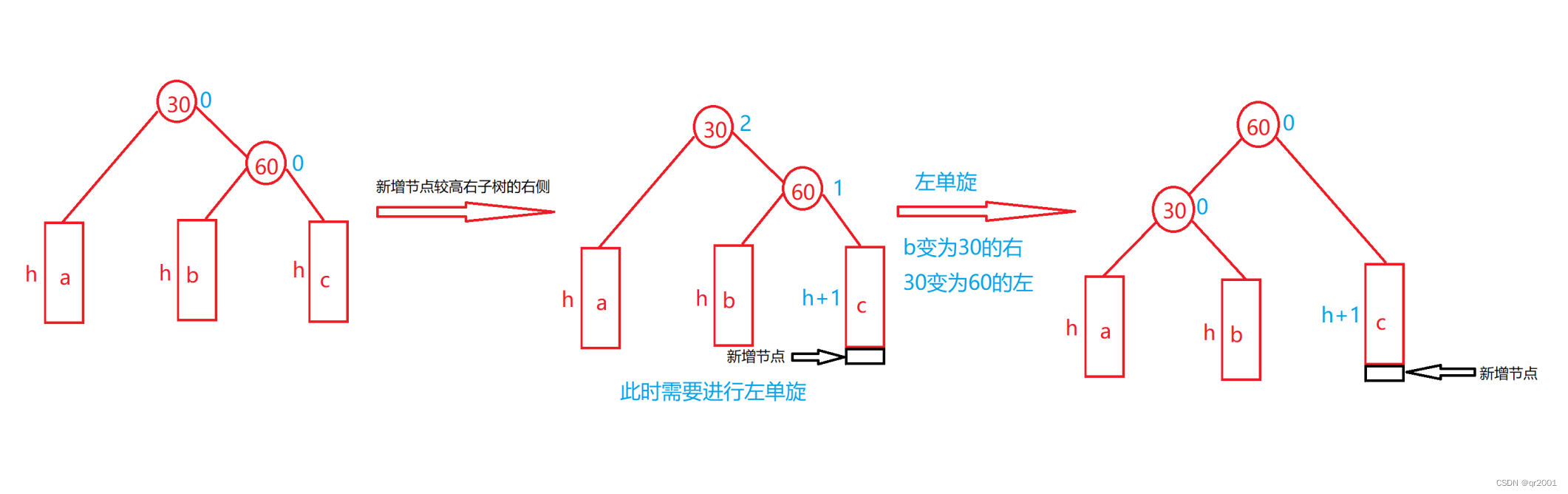
在这里插入图片描述
代码实现

void RotateL(Node* parent)
	{
		Node* SubR = parent->_right;
		Node* SubRL = SubR->_left;

		parent->_right = SubRL;
		if (SubRL)
		{
			SubRL->_parent = parent;
		}

		Node* parentparent = parent->_parent;

		SubR->_left = parent;
		parent->_parent = SubR;

		if (parent == _root)
		{
			_root = SubR;
			SubR->_parent = nullptr;
		}
		else
		{
			if (parent == parentparent->_left)
			{
				parentparent->_left = SubR;
			}
			else
			{
				parentparent->_right = SubR;
			}
			SubR->_parent = parentparent;
		}
		SubRL->_bf = SubR->_bf = 0;

	}

左右双旋

新节点插入较高左子树的右侧—左右
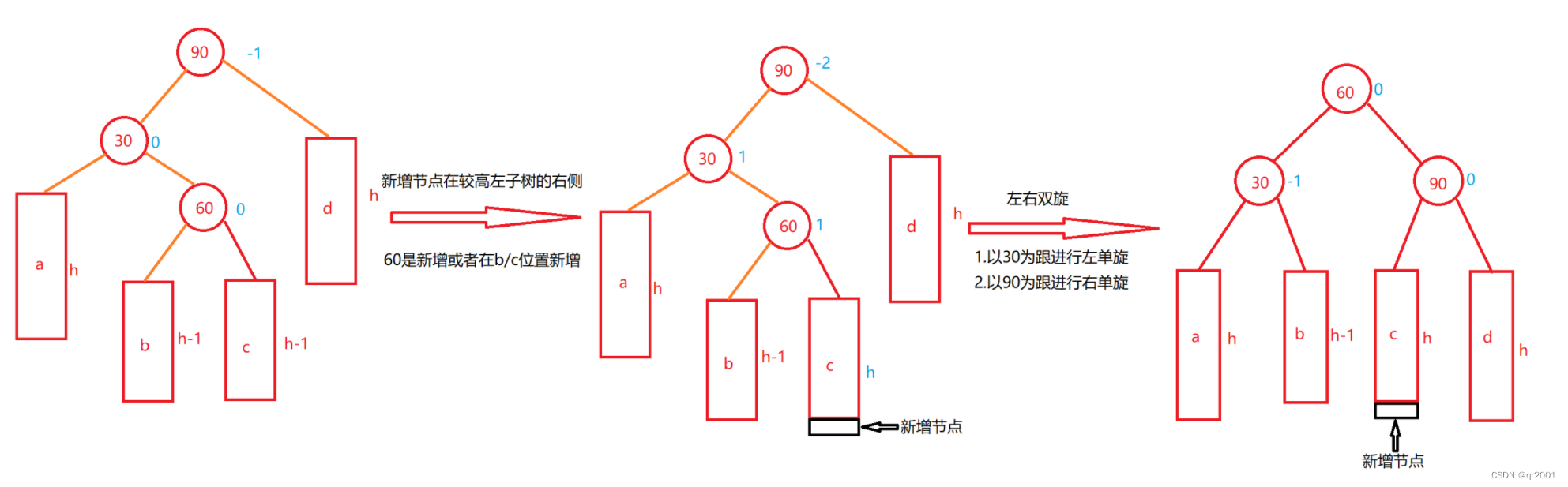
在这里插入图片描述
代码实现

void RotateLR(Node* parent)
	{
		RotateL(parent->_left);
		RotateR(parent);
	}

右左双旋

新节点插入较高右子树的左侧—右左
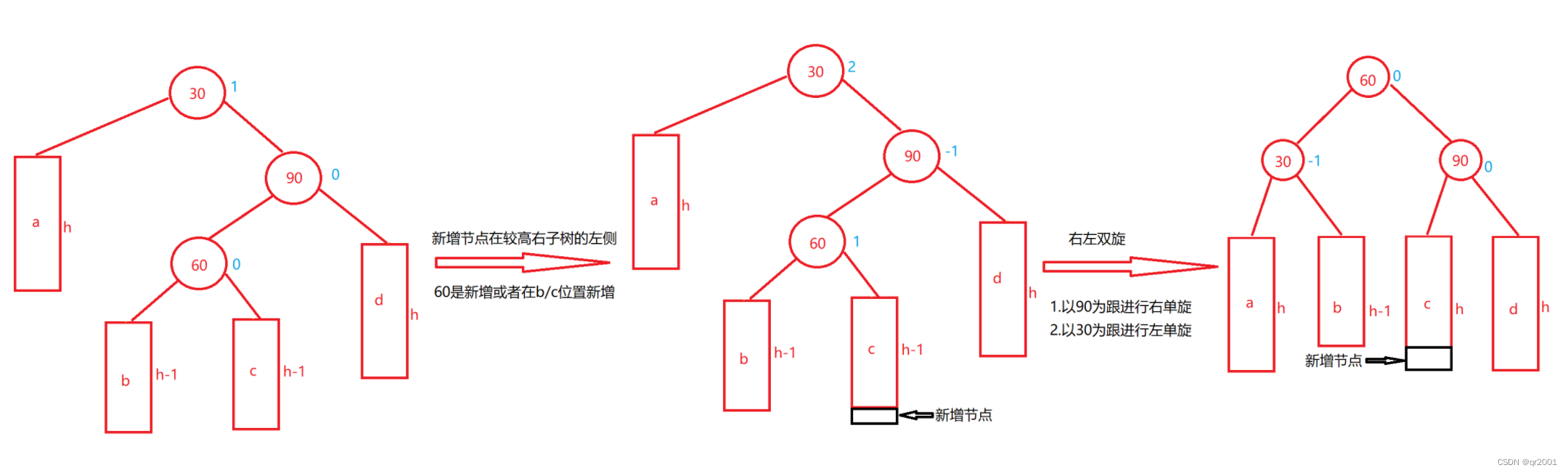
在这里插入图片描述
代码实现

void RotateRL(Node* parent)
	{
		RotateR(parent->_right);
		RotateL(parent);
	}

双旋平衡因子更正

上面的就是针对于插入导致树不平衡之后对其节点进行旋转的处理，那么针对于双旋，我们都是举例插在C的位置，那么当h要是等于0和h等于一的时候插入在b/c不同的位置，又需要对平衡因子进行更正

左右双旋

在这里插入图片描述
针对于以上三种情况，我们要对平衡因子进行处理

void RotateLR(Node* parent)
	{
		Node* Subl = parent->_left;
		Node* SubLR = Subl->_right;
		int bf = SubLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == -1)
		{
			parent->_bf = 1;
			Subl->_bf = 0;
			SubLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			Subl->_bf = -1;
			SubLR->_bf = 0
		}
		else if (bf == 0)
		{
			parent->_bf = Subl->_bf = SubLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

右左双旋

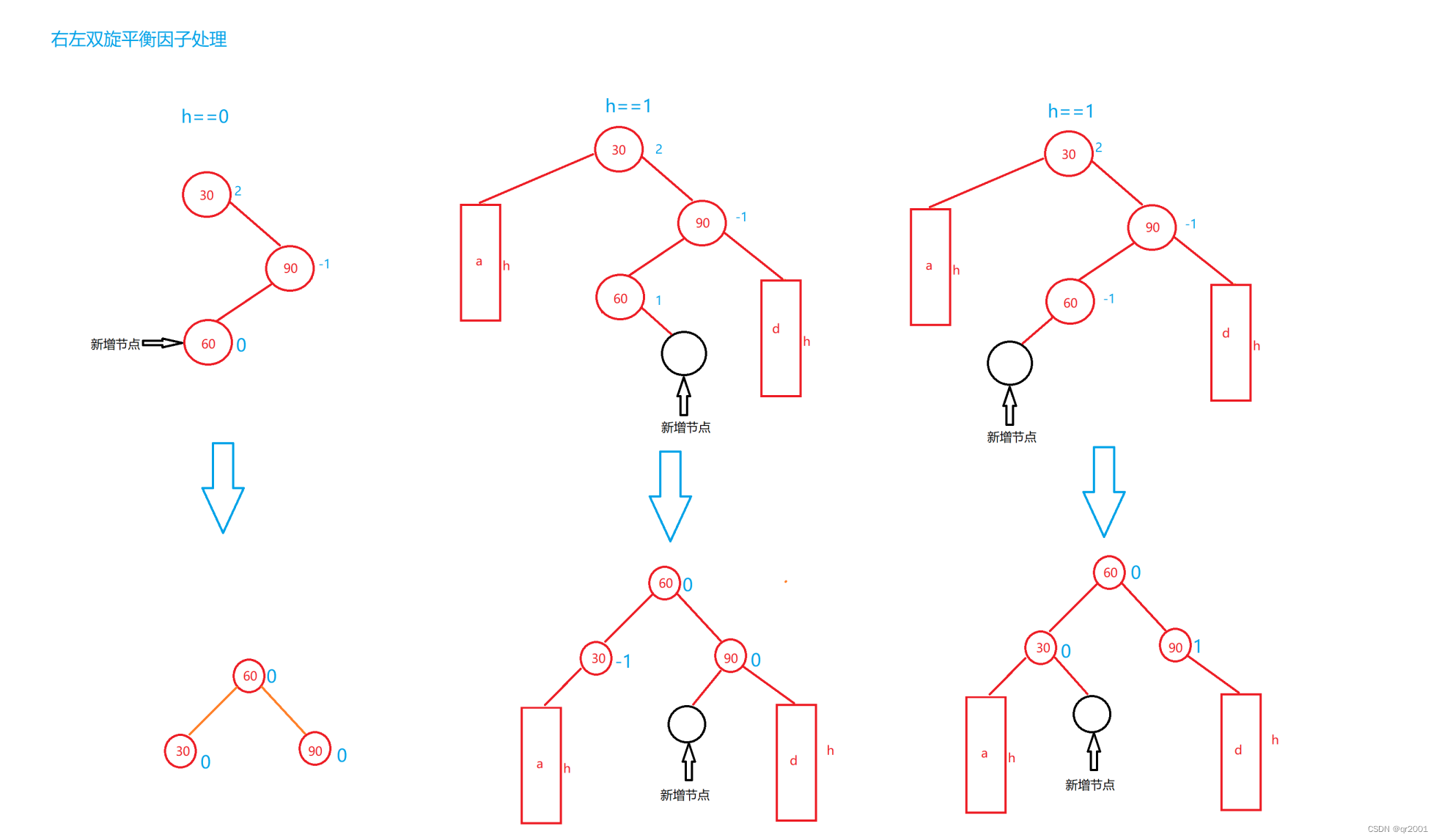
在这里插入图片描述
针对于以上三种情况，我们还是要对平衡因子进行处理

void RotateRL(Node* parent)
	{
		Node* SubR = parent->_right;
		Node* SubRL = SubR->_left;
		int bf = SubRL->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 1)
		{
			parent->_bf = -1;
			SubR->_bf = 0;
			SubRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			SubR->_bf = 1;
			SubRL->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = SubR->_bf = SubRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

完整代码

#pragma once
#include<assert.h>
template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	int _bf;//平衡因子  balance factor

	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:

	AVLTree()
		:_root(nullptr)
	{}

	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(KV);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;

		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			cur->_parent = parent;
			parent->_right = cur;
		}
		else
		{
			cur->_parent = parent;
			parent->_left = cur;
		}


		//接下来需要控制平衡
		while (parent)
		{
			if (cur == parent->_left)
			{
				parent->_bf--;
			}
			else
			{
				parent->_bf++;
			}

			if (parent->_bf == 0)//平衡因子等于0的时候就说明这里插入的位置是正确的，直接跳出
			{
				break;
			}
			//平衡因子等于1或-1的时候，此时需要向上调整
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = parent->_parent;
			}
			//平衡因子等于2或-2的时候，此时需要旋转处理
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//右单旋
				if (parent->_bf == -2 && cur->_bf == -1)
				{
					RotateR(parent);
				}
				//左单旋
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);
				}
				else
				{
					assert(false);
				}
			}
			else
			{
				//当走到这里的时候就说明原本的树就有问题,直接报错
				assert(false);
			}

		}

		return true;
	}

	//右单旋
	void RotateR(Node* parent)
	{
		Node* SubL = parent->_left;
		Node* SubLR = SubL->_right;

		parent->_left = SubLR;
		//此时SubLR可能为空
		if (SubLR)
		{
			SubLR->_parent = parent;
		}

		Node* parentparent = parent->_parent;

		SubL->_right = parent;
		parent->_parent = SubL;

		if (parent == _root)
		{
			_root = SubL;
			SubL->_parent = nullptr;
		}
		else
		{
			if (parent == parentparent->_left)
			{
				parentparent->_left = SubL;
				SubL->_parent = parentparent;
			}
			else
			{
				parentparent->_right = SubL;
				SubL->_parent = parentparent;
			}
		}
		parent->_bf = SubL->_bf = 0;
	}

	void RotateL(Node* parent)
	{
		Node* SubR = parent->_right;
		Node* SubRL = SubR->_left;

		parent->_right = SubRL;
		if (SubRL)
		{
			SubRL->_parent = parent;
		}

		Node* parentparent = parent->_parent;

		SubR->_left = parent;
		parent->_parent = SubR;

		if (parent == _root)
		{
			_root = SubR;
			SubR->_parent = nullptr;
		}
		else
		{
			if (parent == parentparent->_left)
			{
				parentparent->_left = SubR;
			}
			else
			{
				parentparent->_right = SubR;
			}
			SubR->_parent = parentparent;
		}
		SubRL->_bf = SubR->_bf = 0;

	}

	void RotateLR(Node* parent)
	{
		Node* Subl = parent->_left;
		Node* SubLR = Subl->_right;
		int bf = SubLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == -1)
		{
			parent->_bf = 1;
			Subl->_bf = 0;
			SubLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			Subl->_bf = -1;
			SubLR->_bf = 0
		}
		else if (bf == 0)
		{
			parent->_bf = Subl->_bf = SubLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	void RotateRL(Node* parent)
	{
		Node* SubR = parent->_right;
		Node* SubRL = SubR->_left;
		int bf = SubRL->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 1)
		{
			parent->_bf = -1;
			SubR->_bf = 0;
			SubRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			SubR->_bf = 1;
			SubRL->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = SubR->_bf = SubRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

private:
	Node* _root;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/162990.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

javaEE学生教学实习计划申报系统Myeclipse开发mysql数据库web结构jsp编程计算机网页项目

javaEE学生教学实习计划申报系统Myeclipse开发mysql数据库web结构jsp编程计算机网页项目

一、源码特点 javaEE学生教学实习计划申报系统 是一套完善的web设计系统&#xff0c;对理解JSP java编程开发语言有帮助&#xff0c;系统具有完整的源代码和数据库&#xff0c;系统主要采用B/S模式开发。开发环境为TOMCAT7.0,Myeclipse8.5开发&#xff0c;数据库为Mysql&…
阅读更多...
正点原子【第四期】手把手教你学 Linux之驱动开发篇-01

正点原子【第四期】手把手教你学 Linux之驱动开发篇-01

学习目的 了解驱动开发和应用开发的过程&#xff0c;具有一定的基础就行 第一讲&#xff1a;linux驱动开发与裸机开发区别 刚开始听不懂很正常&#xff0c;等之后学了一点你就会知道它说啥了 第二讲&#xff1a;字符设备驱动开发基础 字符设备驱动是最简单的&#xff0c;块设…
阅读更多...
C++ 移动语义

C++ 移动语义

从拷贝说起我们知道&#xff0c;C中有拷贝构造函数和拷贝赋值运算符。那既然是拷贝&#xff0c;听上去就是开销很大的操作。没错&#xff0c;所谓拷贝&#xff0c;就是申请一块新的内存空间&#xff0c;然后将数据复制到新的内存空间中。如果一个对象中都是一些基本类型的数据的…
阅读更多...
【Unity3D】绘制物体外框线条盒子

【Unity3D】绘制物体外框线条盒子

1 需求描述 点选物体、框选物体、绘制外边框 中介绍了物体投影到屏幕上的二维外框绘制方法&#xff0c;本文将介绍物体外框线条盒子绘制方法。 内框&#xff1a;选中物体后&#xff0c;绘制物体的内框&#xff08;紧贴物体、并与物体姿态一致的内框盒子&#xff09;外框&#…
阅读更多...
Python与C++语法比较--字符串篇

Python与C++语法比较--字符串篇

tags: C Python 写在前面 刷lc从Python转向C, 不只是语法层面, 还要改变很多的API, 这次记录一下C和Python在字符串方面的一些区别, 供参考. 基本区别 Python字符串是不可变类型, 而C的String为容器(本质上是一个类的别名, 说容器有点不合适, 因为容器内的元素类型已经被指…
阅读更多...
Kotlin中的Lambda编程

Kotlin中的Lambda编程

文章目录1.集合的创建与遍历2.集合的函数式API3.Java函数式API的使用1.集合的创建与遍历 传统意义上的集合主要是List和Set&#xff0c;再广泛一点的话&#xff0c;像Map这样的键值对数据结构也可以包含进来。List&#xff0c;Set和Map再Java中都是接口&#xff0c;List主要的…
阅读更多...
Java设计模式-命令模式Command

Java设计模式-命令模式Command

介绍 命令模式&#xff08;Command Pattern&#xff09;&#xff1a;在软件设计中&#xff0c;我们经常需要向某些对象发送请求&#xff0c;但是并不知道请求的接收 者是谁&#xff0c;也不知道被请求的操作是哪个&#xff0c; 我们只需在程序运行时指定具体的请求接收者即可&…
阅读更多...
数影周报：TikTok因在线跟踪被罚500万欧，Windows 7退出历史舞台

数影周报：TikTok因在线跟踪被罚500万欧，Windows 7退出历史舞台

本周看点&#xff1a;TikTok因在线跟踪被法国罚款500万欧元 &#xff1b;思科已裁员近700 人&#xff1b;Windows 7退出历史舞台&#xff1b;亚马逊向所有卖家开放Buy with Prime服务&#xff1b;“全路程”完成2亿元C轮融资......数据安全那些事TikTok因在线跟踪被法国罚款500…
阅读更多...
Android13 wifi无线调试adb连接设置

Android13 wifi无线调试adb连接设置

在进行adb调试的时候&#xff0c;有时候需要使用wifi连接&#xff0c;或者wifi连接较为方便&#xff0c;早些的Android上&#xff0c;需要设置端口等操作&#xff0c;adb tcpip 6666参考android wifi adb 调试 - 简书 (jianshu.com)好几步操作&#xff0c;在Android13上&#x…
阅读更多...
Deque 的理解 STL中stack与queue为什么选择使用deque为底层模板容器

Deque 的理解 STL中stack与queue为什么选择使用deque为底层模板容器

目录 一、Deque的引入 二、Deque是什么&#xff1f; 三、deque的遍历方式&#xff1f;deque的缺陷&#xff1f; 四、它为什么能更贴合与stack与queue&#xff1f; 五、STL中vector与list的底层实现 一、Deque的引入 Stack、Queue在之前的博客中我也是分别使用了更容易处理…
阅读更多...
【蓝桥杯】历届真题 杨辉三角形 （省赛）Java

【蓝桥杯】历届真题 杨辉三角形 （省赛）Java

【问题描述】 下面的图形是著名的杨辉三角形: 如果我们按从上到下、从左到右的顺序把所有数排成一列&#xff0c;可以得到如下数列: 1,1&#xff0c;1&#xff0c;1&#xff0c;2,1&#xff0c;1&#xff0c;3,3&#xff0c;1&#xff0c;1,4&#xff0c;6,4&#xff0c;1&…
阅读更多...
数字IC设计、验证、FPGA笔试必会 - Verilog经典习题 （六）多功能数据处理器

数字IC设计、验证、FPGA笔试必会 - Verilog经典习题 （六）多功能数据处理器

数字IC设计、验证、FPGA笔试必会 - Verilog经典习题 &#xff08;六&#xff09;多功能数据处理器 &#x1f508;声明&#xff1a; &#x1f603;博主主页&#xff1a;王_嘻嘻的CSDN博客 &#x1f9e8;未经作者允许&#xff0c;禁止转载 &#x1f511;系列专栏&#xff1a;牛客…
阅读更多...
react基础Day02-受控组件评论案例propscontext

react基础Day02-受控组件评论案例propscontext

React组件 目标 能够知道受控组件是什么能够写出受控组件了解非受控组件 表单处理 受控组件&#xff08;★★★&#xff09; HTML中的表单元素是可输入的&#xff0c;也就是有自己的可变状态而React中可变状态通常保存在state中&#xff0c;并且只能通过setState() 方法来…
阅读更多...
[acwing周赛复盘] 第 86 场周赛20230114

[acwing周赛复盘] 第 86 场周赛20230114

[acwing周赛复盘] 第 86 场周赛20230114 一、本周周赛总结二、 4794. 健身1. 题目描述2. 思路分析3. 代码实现三、4795. 安全区域1. 题目描述2. 思路分析3. 代码实现四、4796. 删除序列1. 题目描述2. 思路分析3. 代码实现六、参考链接一、本周周赛总结 去吃羊蝎子了&#xff0…
阅读更多...
基于汽车知识图谱的汽车问答多轮对话系统 详细教程

基于汽车知识图谱的汽车问答多轮对话系统 详细教程

结果： 1 技术路线 该技术路线主要将KBQA分为三部分，实体识别与实体链接，关系识别，sparql查询，其中每个部分分为一到多种方法实现。具体的处理流程图如下：
阅读更多...
大脑的记忆

大脑的记忆

AI神经网络中的记忆 当前AI发展进入一个瓶颈，大家都意识到还是要继续在人脑中获取AI方向的指引。当然也有科学家说物理世界与心理世界并非一一对应，人类的智能也没必要与物理世界一一对应，甚至本质上都可以是不同的，所以没必要研究大脑认知和大脑的机制，更不需要分子级别…
阅读更多...
IDEA structure窗口各标志及功能

IDEA structure窗口各标志及功能

文章目录图标对象类型访问权限其他修饰符工具栏图标 对象类型 class 类 interface 接口 enum 枚举 interface 注解 class initializer 代码块 method 方法 field 字段/属性 anonymous class 匿名类 lambda lambda表达式 propertie 访问器&#xff08;get方法&#xff0…
阅读更多...
【Java面试】Queue接口

【Java面试】Queue接口

文章目录BlockingQueue中有哪些方法&#xff0c;为什么这样设计&#xff1f;BlockingQueue是怎么实现的&#xff1f;BlockingQueue中有哪些方法&#xff0c;为什么这样设计&#xff1f; 先看一眼结构&#xff0c;再看具体的分析 为了应对不同的业务场景&#xff0c;Blockin…
阅读更多...
拉伯证券|业绩猛增超13倍，主力连续抢筹，这只股收获4连板

拉伯证券|业绩猛增超13倍，主力连续抢筹，这只股收获4连板

成绩陡增股获主力接连抢筹 春节日益接近&#xff0c;A股成交活跃度有所下滑&#xff0c;不过有一些股票节前继续取得主力喜爱。证券时报•数据宝核算&#xff0c;到1月12日收盘&#xff0c;沪深两市共54只个股接连5日或5日以上主力资金净流入。 主力资金净流入继续周期最长的是…
阅读更多...
人工智能学习07--pytorch03--tensorboard（下载tensorboard、opencv）

人工智能学习07--pytorch03--tensorboard（下载tensorboard、opencv）

transform 主要是对input图像进行变换&#xff08;统一尺寸、对图像中的数据进行类的转换&#xff09; TensorBoard很有用 如&#xff1a;通过loss的变化过程&#xff0c;来看loss的变化是否复合预想。也可以通过loss来选择模型。 TensorBoard&#xff0c;虽然他是TensorFlo…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023