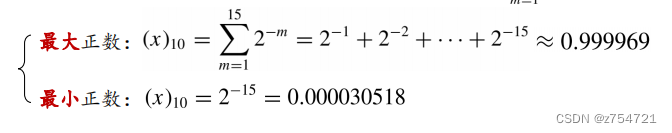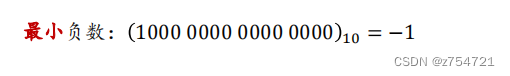-
文章图片内容主要来着老师的PPT,内容为自己总结梳理的学习笔记
-
二进制定点表示与量化误差
-
二进制定点表示
-
基础知识
-
二进制小数的定点表示
-
正数小数的定点表示:
-
-
思考题:推算字长为16的二进制最大正数与二进制正数
-
-
-
-
补码:正数不变,负数为除符号位所有位取反然后加1.(为了允许采用相同硬件来执行的加法和减法)
-
负数小数的定点表示:
-
-
思考题:推算最小16位字长表示下,定点表示的负数是多少?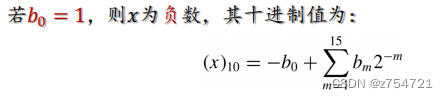
-
-
-
-
-
-
量化误差
-
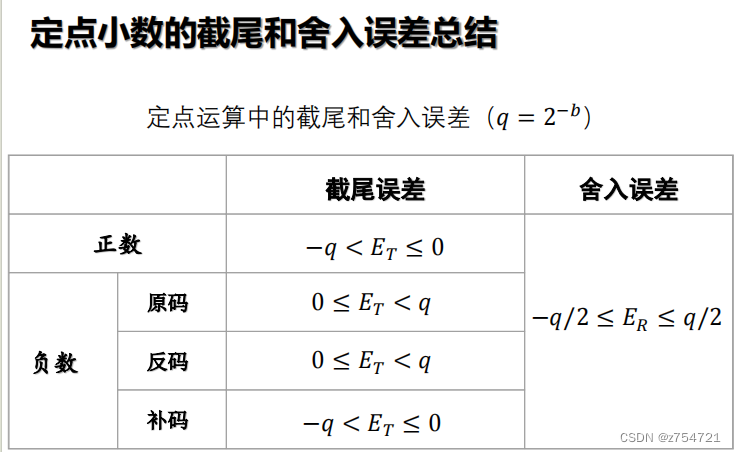
正数的截尾误差:
-
-
负数的截尾误差
-
负数的原码、反码、补码表示法不同,所以量化影响也不同
-
原码的量化误差(截尾后负小数的绝对值变小,截尾误差为正):
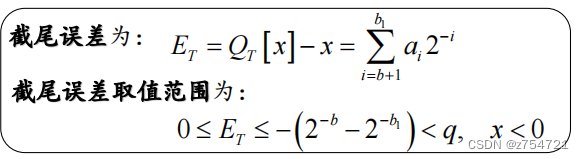
-
反码:
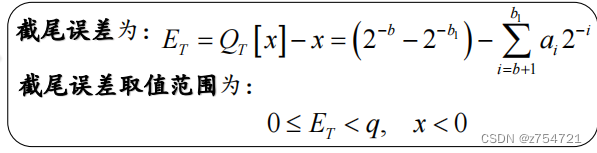
-
补码:
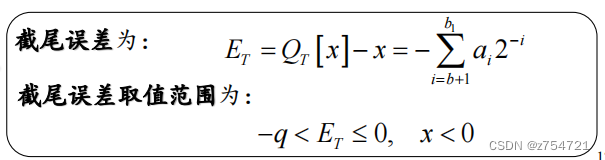
-
-
-
结论:1)原码与反码的截尾误差与数的正负有关;2)补码的截尾误差解释负数

-
-
-
-
A/D转化器中的量化误差
-
量化误差的统计分析
-

-
量化信噪比与所需字长的关系
-
字长每增加1位,信噪比增加约6db
-
-
量化噪声通过LTI系统
-

-
-
系数量化对数字滤波器的影响
-
系数量化器对IIR系统极点的影响
-
前提:实际设计中,传递函数的系数需要定点量化
-
影响:零极点位置的移动,实际频率响应不等于理想频率响应尤其当极点靠近单位圆是,导致的稳定性问题
-
直接型:系数与零极点的关系不直接,不易控制和调制滤波器的性能
-
级联型:可单独调制滤波器的第k对临极点而不影响其他零极点
-
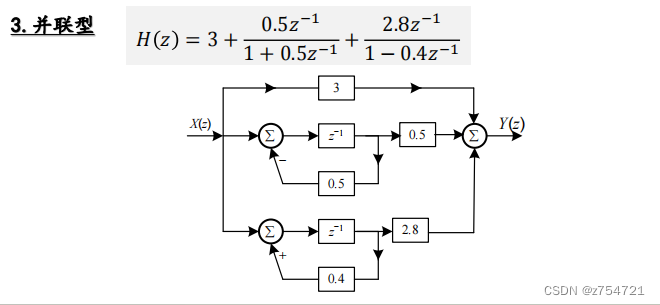
并联型(传递函数部分分式展开):可单独调制第k对极点位置,各子系统的误差互不影响,运算累计误差小
-
例题:试画出该传递函数的直接型,级联型和并联型的模拟框图
-

-

-
-
-
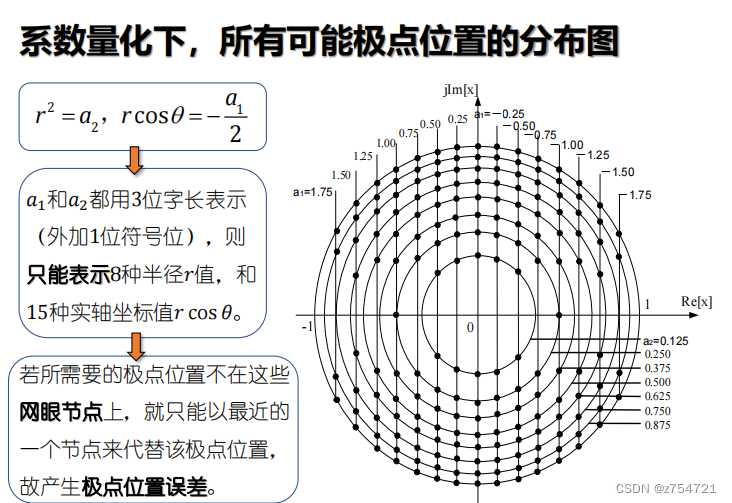
系数量化对二阶子系统对极点位置的影响:
-

-
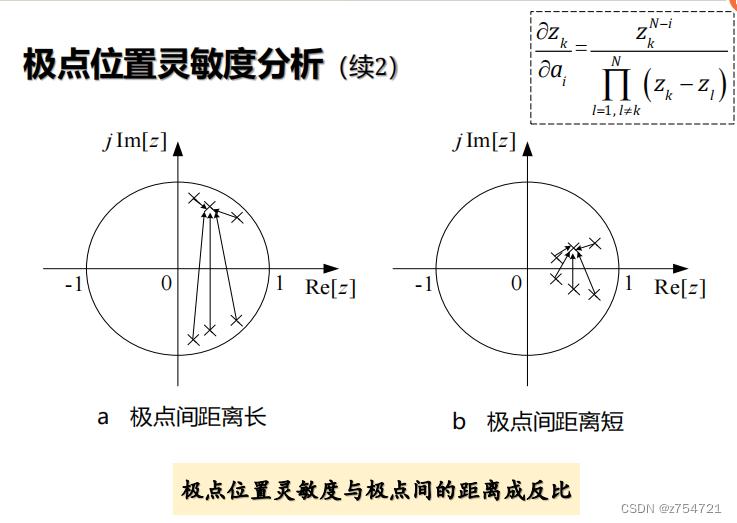
总结:1.一般,较高阶的IIR传输函数不适合用直接型结构实现,可以通过二阶系统和一阶系统的级联型结构来实现;2.重点关注二阶系统的乘法器系数量化所引起的极点偏移;若极点在系数量化后离原始位置很近,则该结构具有低极点灵敏度,反之则有高极点灵敏度
-
二阶网络结构(直接型与耦合型)
-

-

-
-
极点位置灵敏度分析
-
-
-
运算量化效应
-
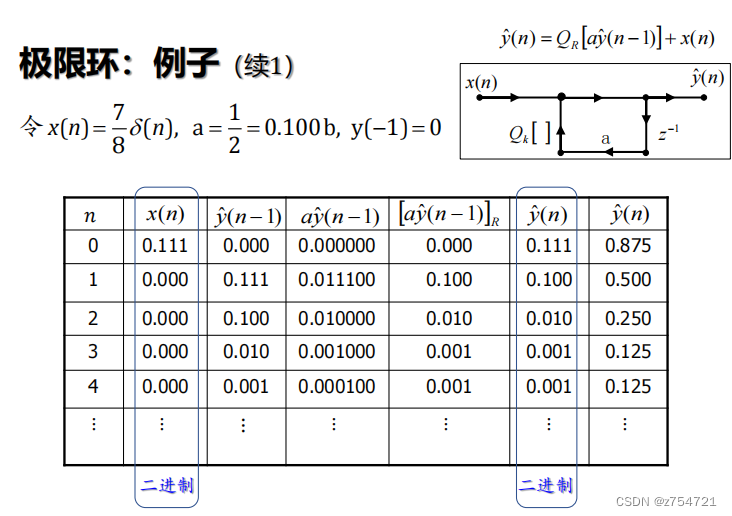
零输入极限环:对于IIR滤波器,在无限精度的情况下当所有极点都位于单位圆内时,系统稳定 • 若稳定,去掉输入信号后,随着时间推移,系统输出逐渐衰减趋于零 • 然而,在有限字长的情况下 • 量化过程产生非线性作用 • 即便稳定,去掉输入信号后,系统输出将不随时间衰减趋于零,而是衰 减到某一个非零的幅度范围内
-
例子:
-
-
DSP技术及应用——学习笔记一(量化效应)
news2026/2/13 16:58:38
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1624288.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
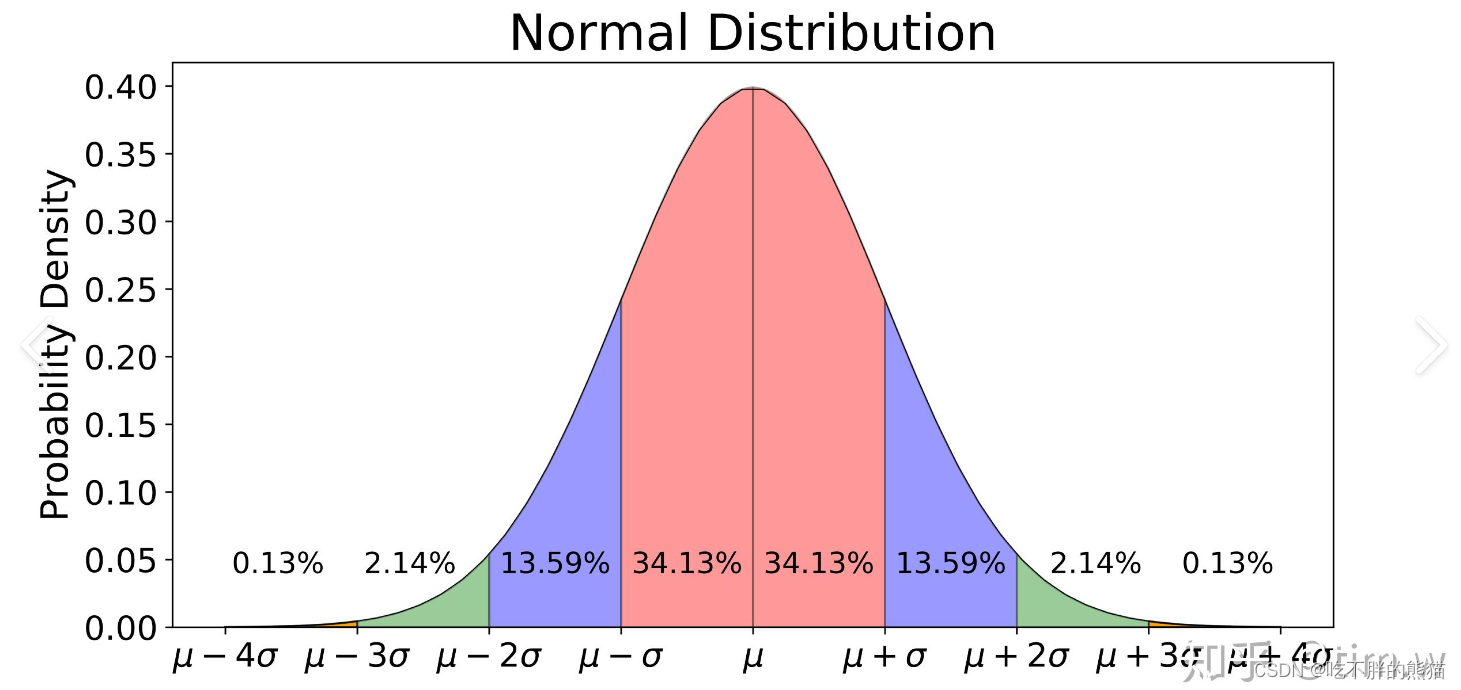
【AI相关】数学和统计学知识
数学和统计学的知识可以分为两部分:
一部分是线性代数中的基础概念,比如标量、向量和张量。
另一部分是概率统计中常见的分布类型,比如正态分布和伯努利分布。 线性代数
什么是标量?
标量是一个单独的数,可以是整…
matlab新手快速上手6(引力搜索算法)
本文根据一个较为简单的matlab引力搜索算法框架详细分析蚁群算法的实现过程,对matlab新手友好,源码在文末给出。
引力搜索算法简介: 引力搜索算法是一种启发式优化算法,最初于2009年由伊朗的Esmat Rashedi、Hossein Nezamabadi-p…
Vitis HLS 学习笔记--HLS入门示例集合-目录
目录
1. 示例集合概述
2. Interface 接口
2.1 Aggregation_Disaggregation 聚合与解聚
2.1.1 aggregation_of_m_axi_ports
2.1.2 aggregation_of_nested_structs
2.1.3 aggregation_of_struct
2.1.4 auto_disaggregation_of_struct
2.1.5 disaggregation_of_axis_port …
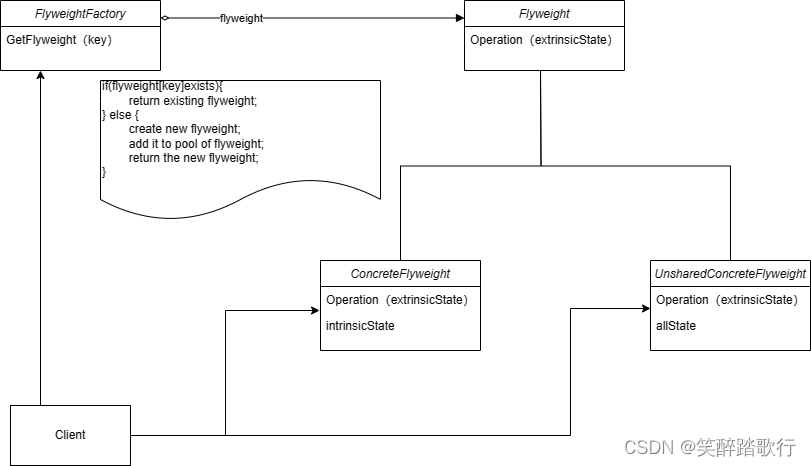
2.6设计模式——Flyweight 享元模式(结构型)
意图
运用共享技术有效地支持大量细粒度的对象。
结构 其中
Flyweight描述一个接口,通过这个接口Flyweight可以接受并作用于外部状态。ConcreteFlyweight实现Flyweight接口,并作为内部状态(如果有)增加存储空间。ConcreteFlywe…
6547网新增信息素养大赛真题及白名单考级真题
打扰大家了,汇报一下最近的更新动态,如果大家有急切需要的白名单真题及试卷留言,我们会优先更新! 6547网文库(www.6547.cn/wenku):新增信息素养大赛图形化编程真题及Python真题,2024…
STM32单片机C语言模块化编程实战:LED控制详解与示例
一、开发环境
硬件:正点原子探索者 V3 STM32F407 开发板
单片机:STM32F407ZGT6
Keil版本:5.32
STM32CubeMX版本:6.9.2
STM32Cube MCU Packges版本:STM32F4 V1.27.1
之前介绍了很多关于点灯的方法,比如…
不要小看使用说明书,它才是提高成交率的秘诀
在产品推广和销售环节中,许多企业可能忽略了一个非常重要但常被低估的环节——使用说明书的作用。使用说明书,这本附随每件产品的“小书”,往往是用户了解和使用产品的第一步。事实上,一个清晰、详尽、易懂的使用说明书能够显著提…
Blueprints - 鼠标光标判断相关节点
一些以前的学习笔记归档; 俯视角场景中要用鼠标光标判断是否点中物体,或依靠光标引发各种事件;
这些逻辑一般编写在Controller中,Controller类本身就带有相关判断节点: 其中Get Hit Result Under Cursor by Channel是…
OpenFeign微服务调用组件!!!
1.Feign是什么
GitHub - OpenFeign/feign: Feign makes writing java http clients easierFeign makes writing java http clients easier. Contribute to OpenFeign/feign development by creating an account on GitHub.https://github.com/OpenFeign/feignFeign是Netflix开…
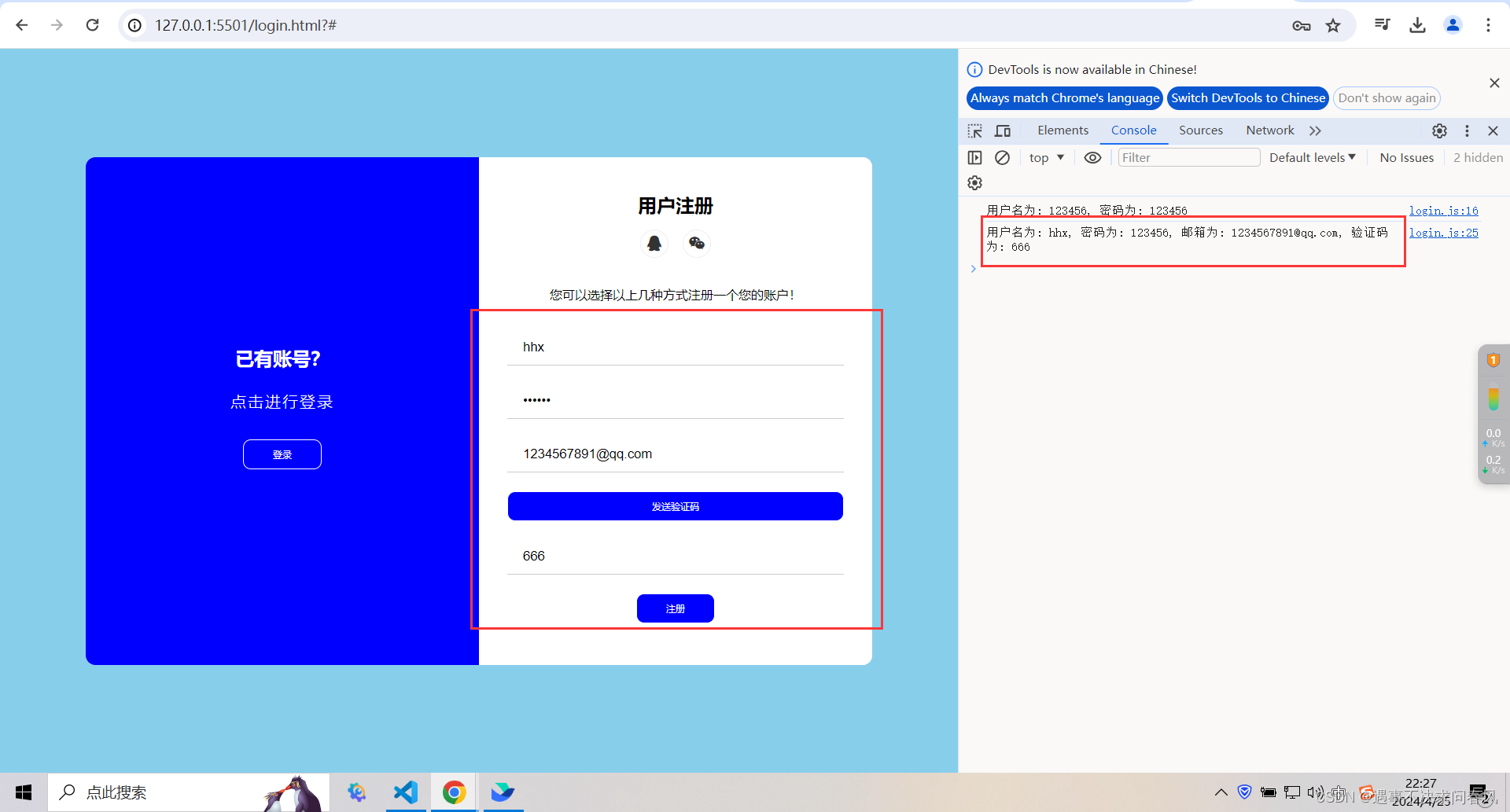
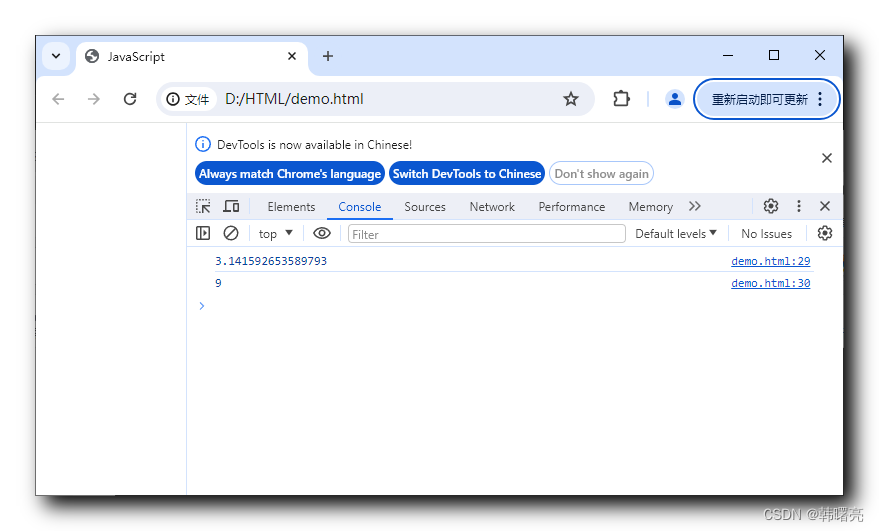
JavaScript:将input标签中的内容打印到控制台
使用浏览器进行开发时,按F12可以查看网页信息。
目标:实现将input标签中的内容,打印到控制台(console)
HTML页面的关键代码实现:
登录功能:
HTML代码: <div class"form-…
个人博客系统的设计与实现
https://download.csdn.net/download/liuhaikang/89222885http://点击下载源码和论文 本 科 毕 业 设 计(论文) 题 目:个人博客系统的设计与实现 专题题目: 本 科 毕 业 设 计(论文)任 务 书 题 …
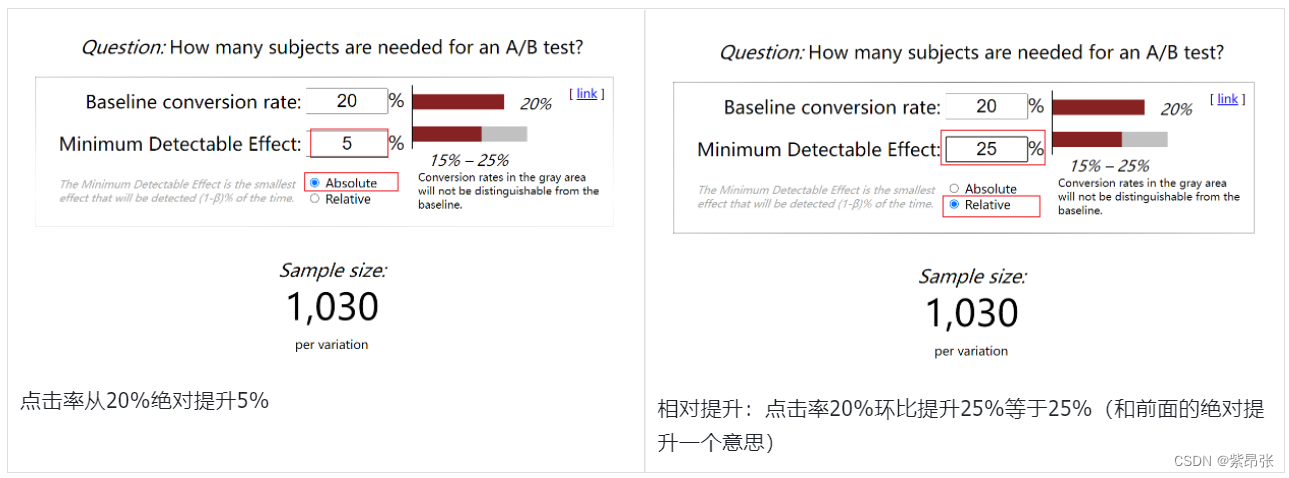
ABTest如何计算最小样本量-工具篇
如果是比例类指标,有一个可以快速计算最小样本量的工具:
https://www.evanmiller.org/ab-testing/sample-size.html 计算样本量有4个要输入的参数:①一类错误概率,②二类错误概率 (一般是取固定取值)&…
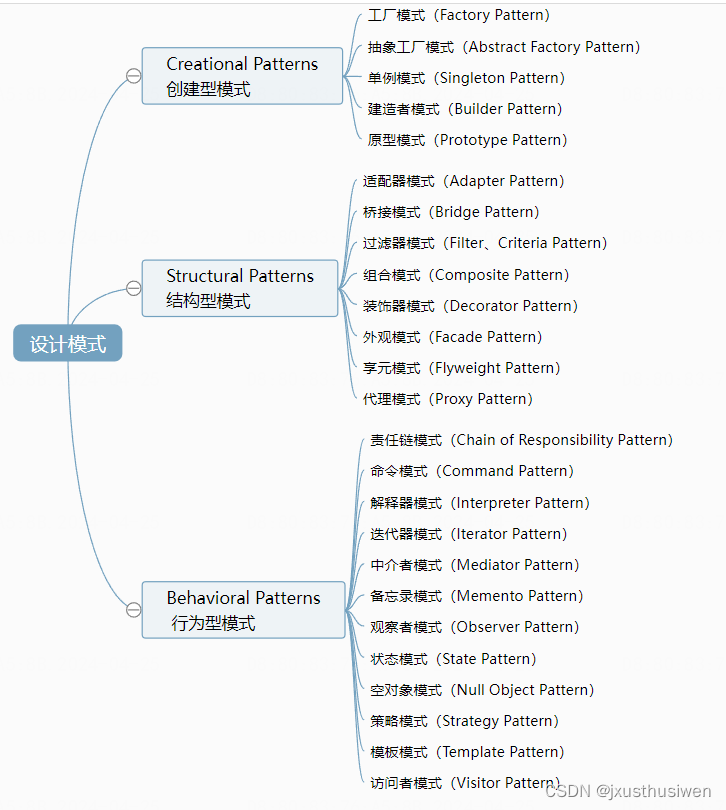
设计模式-01 设计模式简介之分类
设计模式-01 设计模式简介之分类 1.分类概述 今天梳理下设计模式的分类学说。按照GoF书籍 《Design Patterns - Elements of Reusable Object-Oriented Software》(中文译名:《设计模式 - 可复用的面向对象软件元素》) 中所提到的,…
牛客NC209 最短无序连续子数组【中等 数组,双指针 C++/Java/Go/PHP】
题目 题目链接: https://www.nowcoder.com/practice/d17f4abd1d114617b51e951027be312e
思路
解题思路
1、方法1,排序对比:将数组按升序排序,然后与原数组对照,从哪里开始变化到哪里结束变化的数组就是答案。
2、 方…
初识 Express
目录
1. Express 简介
1.1. 什么是 Express
1.1.1. 概念
1.1.2. 通俗理解
1.1.3. Express 的本质
1.2. 进一步理解 Express
1.2.1. 问题引入1——不使用 Express 能否创建 Web 服务器?
1.2.2. 问题引入2——有了 http 内置模块,为什么还要用 Exp…
【算法刷题 | 贪心算法03】4.25(最大子数组和、买卖股票的最佳时机|| )
文章目录 4.最大子数组和4.1题目4.2解法一:暴力4.2.1暴力思路4.2.2代码实现 4.3解法二:贪心4.3.1贪心思路4.3.2代码实现 5.买卖股票的最佳时机||5.1题目5.2解法:贪心5.2.1贪心思路5.2.2代码实现 4.最大子数组和
4.1题目
给你一个整数数组 n…
【JavaScript】内置对象 ③ ( Math 内置对象 | Math 内置对象简介 | Math 内置对象的使用 )
文章目录 一、Math 内置对象1、Math 内置对象简介2、Math 内置对象的使用 二、代码示例1、代码示例 - Math 内置对象的使用2、代码示例 - 封装 Math 内置对象 一、Math 内置对象 1、Math 内置对象简介 JavaScript 中的 Math 内置对象 是一个 全局对象 , 该对象 提供了 常用的 数…
openEuler-22.03下载、安装
一、下载
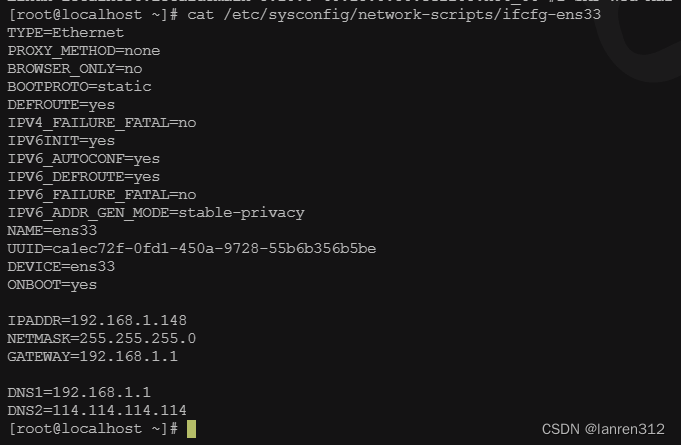
下载地址:openEuler下载 | 欧拉系统ISO镜像 | openEuler社区官网 下载版本:openEuler-22.03-LTS-x86_64-dvd.iso 二、安装 配置完后开启虚拟机 设置完后,重启虚拟机 设置桥接模式的网络
cd /etc/sysconfig/network-scripts/
vi if…