文章目录
- 4.最大子数组和
- 4.1题目
- 4.2解法一:暴力
- 4.2.1暴力思路
- 4.2.2代码实现
- 4.3解法二:贪心
- 4.3.1贪心思路
- 4.3.2代码实现
- 5.买卖股票的最佳时机||
- 5.1题目
- 5.2解法:贪心
- 5.2.1贪心思路
- 5.2.2代码实现
4.最大子数组和
4.1题目
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
- 示例一:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
- 示例二:
输入:nums = [1]
输出:1
4.2解法一:暴力
4.2.1暴力思路
- 两层for循环,第一层为起点,第二层为终点
- 注意:该方法只能算数组任意一个元素到数组末尾的最大值,不能指派到任意一个终点
4.2.2代码实现
public int maxSubArray(int[] nums) {
int res=Integer.MIN_VALUE;
for(int i=0;i<nums.length;i++){
int sum=0;
for(int j=i;j<nums.length;j++){
sum+=nums[j];
}
res=Math.max(res,sum);
}
return res;
}
- 注意:
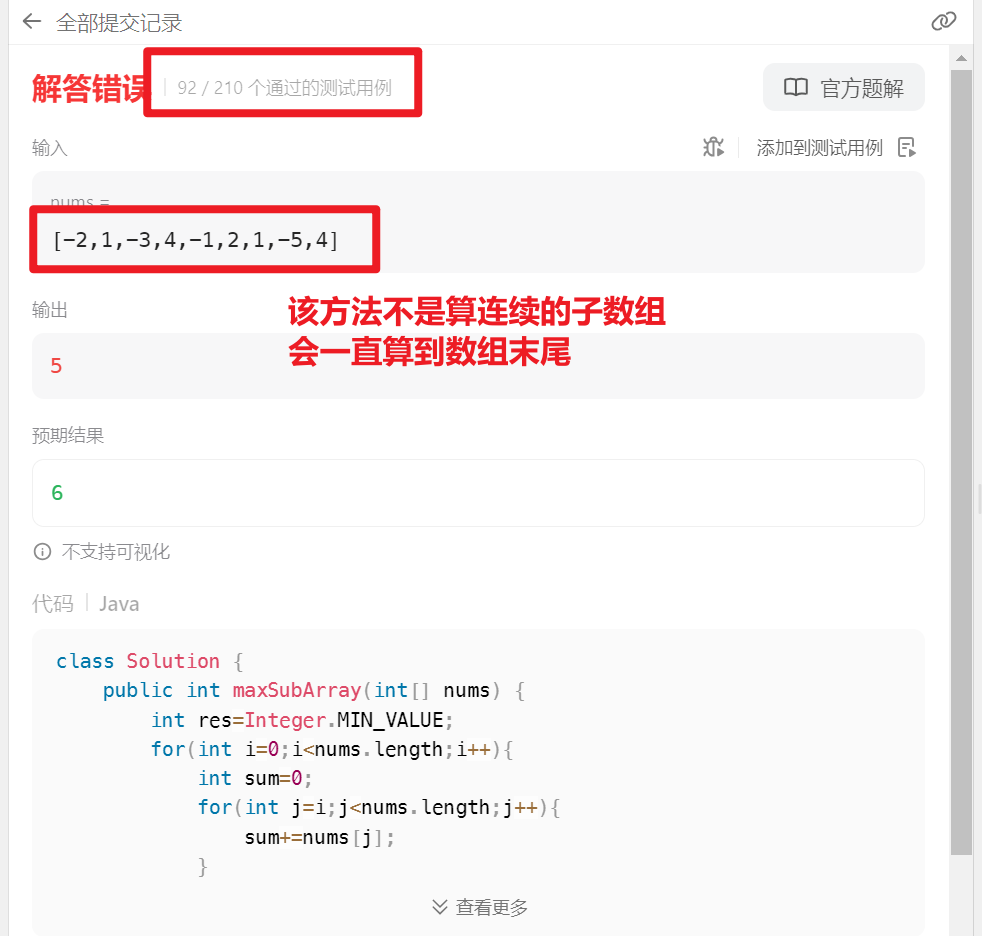
4.3解法二:贪心
4.3.1贪心思路
- 贪心贪在哪里:如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
- 局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
- 全局最优:选取最大“连续和”
4.3.2代码实现
public int maxSubArray(int[] nums) {
int res=Integer.MIN_VALUE; //全局最大连续和
int count=0; //局部最大连续和
for(int i=0;i<nums.length;i++){
//先加上此数
count+=nums[i];
if(count>res){
//更新全局最优解
res=count;
}
//若局部最大连续和为负数,则重置为0,代表从下一位开始计算
if(count<0){
count=0;
}
}
return res;
}
5.买卖股票的最佳时机||
5.1题目
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
- 示例一:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
- 示例二:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
5.2解法:贪心
5.2.1贪心思路
- 平常思想:选一个低的买入,再选个高的卖,再选一个低的买入…循环反复
- 但是最终利润是可以分解的
- 例如:
- 假如第 0 天买入,第 3 天卖出,那么利润为:prices[3] - prices[0]。
- 相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。
- 此时就是把利润分解为每天为单位的维度,而不是从 0 天到第 3 天整体去考虑!
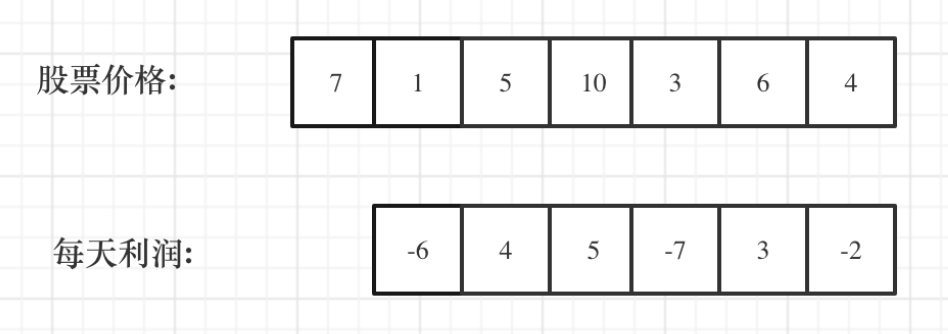
最终的利润:4+5+3=12
从图中可以发现,其实我们需要收集每天的正利润就可以,收集正利润的区间,就是股票买卖的区间,而我们只需要关注最终利润,不需要记录区间。
5.2.2代码实现
public int maxProfit(int[] prices) {
int res=0;
//从第二天开始
for(int i=1;i<prices.length;i++){
//利润取正整数
res+=Math.max(prices[i]-prices[i-1],0);
}
return res;
}