数学和统计学的知识可以分为两部分:
一部分是线性代数中的基础概念,比如标量、向量和张量。
另一部分是概率统计中常见的分布类型,比如正态分布和伯努利分布。
线性代数
什么是标量?
标量是一个单独的数,可以是整数、实数或复数。
它就像是一个单独的点,没有方向,只有大小。
什么是向量?
向量是一组有序的标量,它们按照一定的顺序排列。
你可以把向量想象成一条有方向的线段,线段上的每个点都代表一个标量。
向量可以看作是标量的扩展,
因为它给标量增加了一个维度,让标量从一个单独的数变成了一个有序的数列。
什么是矩阵?
矩阵是由多个向量组成的,这些向量可以是行向量或列向量。
你可以把矩阵想象成一个二维的表格,表格中的每个元素都是一个标量。
矩阵可以看作是向量的扩展,
因为它给向量增加了一个维度,让向量从一个一维的数组变成了一个二维的表格。
什么是张量?
如果我们把矩阵中的每个标量元素再替换成向量,那么我们就得到了一个张量。
张量可以看作是矩阵的扩展,因为它给矩阵增加了一个或多个维度。
换句话说,张量是矩阵向任意维度的扩展。
简单来说,
标量是单个的数,
向量是一组有序的标量,
矩阵是由多个向量组成的二维表格,
而张量则是矩阵向任意维度的扩展。
概率统计
最常见的概率分布包括伯努利分布、二项分布、泊松分布和正态分布;
什么是伯努利分布?
伯努利分布,也叫零一分布,
描述的是只有两种可能结果(通常是成功和失败,用0和1表示)的随机实验。
比如抛硬币,正面是1(成功),反面是0(失败)。
这种分布常用于描述这种单次、二选一的情况。
什么是二项分布?
二项分布则是当伯努利实验重复多次,并且每次实验都是独立的时候,出现特定结果次数(比如硬币正面出现的次数)的概率分布。
如果你抛一个硬币n次,想知道正面出现0次、1次、2次...直到n次的概率是多少,那么这就是二项分布要解决的问题。
每次抛硬币都是一个独立的伯努利实验,而二项分布描述了这些独立实验累积结果的概率分布。
什么是泊松分布?
泊松分布是一种数学工具,用来描述在固定时间或空间内,随机事件发生的次数。
比如,频道页平均每分钟有2000次访问,这就是一个固定时间内的随机事件次数。
泊松分布可以帮助我们计算,在下一分钟里,访问次数达到4000次的可能性有多大。
简单来说,它能帮助我们预测随机事件发生的频率和概率。
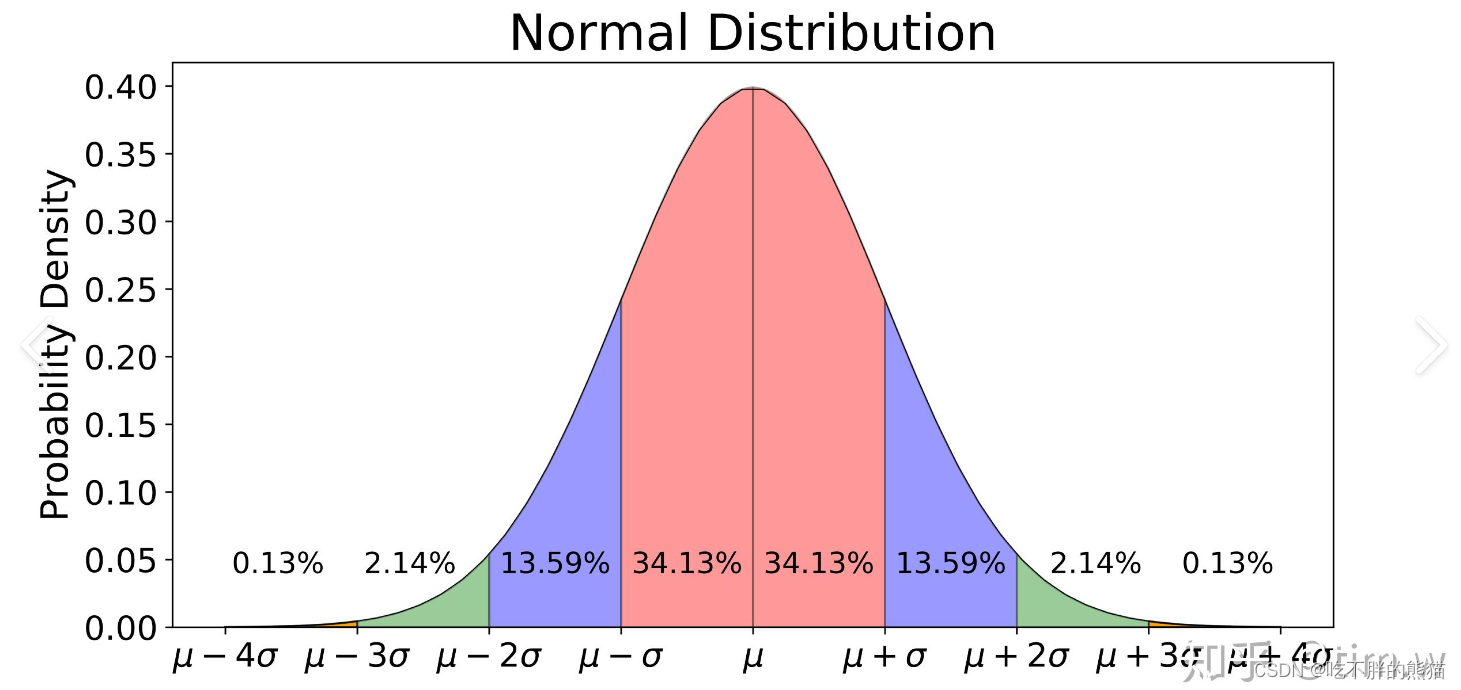
什么是正态分布?
正态分布,也叫高斯分布,是一种常见的数据分布形态。
它的曲线形状特点是两头低、中间高,像一个倒钟形,而且左右两边是对称的。
这意味着数据大多集中在中间,而远离中间的值则相对较少。
这种分布在实际生活中很常见,比如人的身高、考试分数等。