多目标粒子群算法及其MATLAB实现

news2024/10/5 19:14:13

多目标粒子群优化（Multi-Objective Particle Swarm Optimization, MOPSO）算法是一种基于种群的优化算法，它结合了粒子群优化（Particle Swarm Optimization, PSO）和多目标优化的思想。多目标粒子群（MOPSO）算法是由CarlosA. Coello Coello等在2004年提出来的。

以下是对多目标粒子群算法流程的另一种表达方式：

(1) 粒子速度更新机制

粒子速度的更新是基于三个关键组成部分：

  • 惯性部分：它保持了粒子先前的运动方向和速度，有助于粒子保持其运动惯性。
  • 个体认知部分：反映了粒子向其个体历史最佳位置的趋近，体现了粒子的自我学习和调整能力。
  • 社会认知部分：体现了粒子向整个群体中的最佳位置（全局最优）的趋近，反映了粒子间的社会学习和协作。

(2) 粒子位置更新

粒子根据更新后的速度调整其位置，这个过程是粒子在搜索空间中进行探索和寻找更优解的关键步骤。

(3) 个体历史最优位置pbest的选择

对于每个粒子，算法会比较其当前目标函数值和个体历史最优位置的目标函数值。如果两者互不支配，即没有一个在所有目标上都优于另一个，则随机选择一个作为新的历史最优。若存在支配关系，则选择支配的解作为新的历史最优。

(4) 全局最优位置gbest的选择

在多目标优化中，全局最优不是单一的解，而是一组非支配解。MOPSO算法根据非支配解集中的拥挤程度来选择一个全局领导者。选择过程倾向于那些位于较不拥挤区域的粒子，以增加对未知区域的探索。选择概率与粒子的拥挤程度成反比，即粒子所处位置越拥挤，被选择的概率越低。

(5) 非支配解集的更新

在每次迭代后，非支配解集都会进行更新，以确保它包含当前种群中的最佳非支配解。更新过程包括三个步骤：

  1. 初步筛选：首先，根据支配关系去除劣解，只保留非被支配的解，并将它们加入到非支配解集中。
  2. 内部筛选：在非支配解集内部再次根据支配关系进行筛选，进一步去除可能的劣解，并确定每个粒子在网格中的位置。
  3. 数量控制：如果非支配解集的数量超过了设定的阈值，算法会根据自适应网格方法进行筛选，以减少非支配解的数量，直到满足数量限制。随后，重新进行网格划分以适应新的非支配解集。

总体流程图如下:

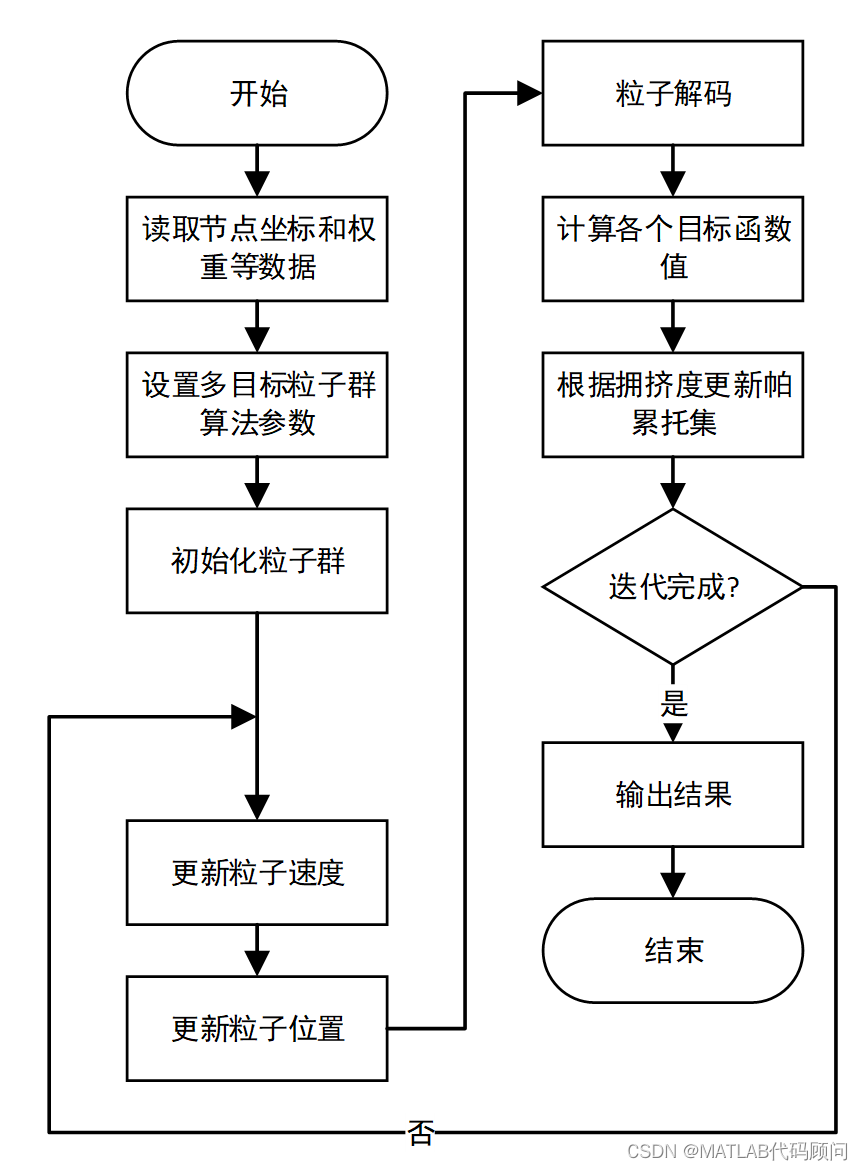
完整代码见: https://download.csdn.net/download/corn1949/89218695

MATLAB主程序部分代码如下:


%% 多目标粒子群算法

% 清除所有变量，关闭所有图形窗口，关闭所有警告信息
clc; close all; clear all; warning off;

% 设置随机数生成器的种子，以确保结果的可重复性
rand('seed', 100);
randn('seed', 100);

% 设置数值显示格式为长精度科学计数法
format long g;

% 定义变量的下界和上界
lb = -4 * ones(1, 5);
ub = 4 * ones(1, 5);

% 定义速度的下界和上界
vlb = (ub - lb) * -0.05;
vub = (ub - lb) * 0.05;

% 获取变量的维度
dimension = length(lb);

% 定义问题的目标数（这里设置为2，表示有两个优化目标）
N = 2;

%% 多目标粒子群算法参数设置

% 种群大小
popsize = 50;

% 帕累托集的大小
nRep = 20;

% 最大迭代次数
maxgen = 100;

% 定义算法中的一些参数
phi1 = 2.05;
phi2 = 2.05;
phi = phi1 + phi2;
chi = 2 / (phi - 2 + sqrt(phi^2 - 4 * phi));
w = chi;  % 惯性权重
wdamp = 1;  % 惯性权重阻尼比
c1 = chi * phi1;  % 个体学习系数
c2 = chi * phi2;  % 全局学习系数
alpha = 0.1;  % 网格膨胀参数
nGrid = 10;  % 每一维的网格数
beta = 4;  % 选择压力参数
gamma = 2;  % 帕累托集选择被删除的压力参数

%% 初始化粒子群

% 生成初始粒子和速度
[psomat, vmat] = genchrom(popsize, dimension, lb, ub, vlb, vub);
particle = CreateEmptyParticle(popsize);

% 初始化每个粒子的速度、位置、成本和最佳位置
for i = 1:popsize
    particle(i).Velocity = vmat(i, :);
    particle(i).Position = psomat(i, :);
    particle(i).Cost = myfun(particle(i).Position);
    particle(i).Best.Position = particle(i).Position;
    particle(i).Best.Cost = particle(i).Cost;
end

% 确定粒子间的支配关系
particle = DetermineDomination(particle);

% 获取非支配粒子
rep = GetNonDominatedParticles(particle);
rep_costs = GetCosts(rep);

% 创建超立方体网格
G = CreateHypercubes(rep_costs, nGrid, alpha);

% 为每个非支配粒子分配网格索引
for i = 1:numel(rep)
    [rep(i).GridIndex rep(i).GridSubIndex] = GetGridIndex(rep(i), G);
end

% 初始化记录每代最佳和平均成本的矩阵
trace_best_mat = zeros(maxgen, N);
trace_mean_mat = zeros(maxgen, N);

%% MOPSO主循环

wait_hand = waitbar(0, 'running...', 'tag', 'TMWWaitbar');
for gen = 1:maxgen
    for i = 1:popsize
        % 选择领导者粒子
        rep_h = SelectLeader(rep, beta);
        
        % 更新粒子的速度
        V = particle(i).Velocity;
        V = w * V + c1 * rand * (particle(i).Best.Position - particle(i).Position) + c2 * rand * (rep_h.Position - particle(i).Position);
        V = limitspeed(V, vlb, vub, dimension);
        particle(i).Velocity = V;
        
        % 更新粒子位置
        p = particle(i).Position;
        p = p + V;
        p = limitposition(p, lb, ub, dimension);
        particle(i).Position = p;
        particle(i).Cost = myfun(particle(i).Position);
        
        % 更新粒子的最佳位置
        if Dominates(particle(i), particle(i).Best)
            particle(i).Best.Position = particle(i).Position;
            particle(i).Best.Cost = particle(i).Cost;
        elseif ~Dominates(particle(i).Best, particle(i)) && rand < 0.5
            particle(i).Best.Position = particle(i).Position;
            particle(i).Best.Cost = particle(i).Cost;
        end
    end
    
    % 确定粒子间的支配关系，并获取非支配粒子
    particle = DetermineDomination(particle);
    nd_particle = GetNonDominatedParticles(particle);
    rep = [rep; nd_particle];
    rep = DetermineDomination(rep);
    rep = GetNonDominatedParticles(rep);
    
    % 为每个非支配粒子分配网格索引
    for i = 1:numel(rep)
        [rep(i).GridIndex rep(i).GridSubIndex] = GetGridIndex(rep(i), G);
    end
    
    % 如果非支配解的数量超过了设定的帕累托集大小，则进行删除操作
    if numel(rep) > nRep
        EXTRA = numel(rep) - nRep;
        rep = DeleteFromRep(rep, EXTRA, gamma);
        rep_costs = GetCosts(rep);
        G = CreateHypercubes(rep_costs, nGrid, alpha);
    end
    
    % 更新惯性权重
    w = w * wdamp;
    
    % 记录每代的最佳和平均成本
    costs20gen=GetCosts(particle);
    % trace_best_mat(gen,:)=min(costs20gen');
    if gen==1
        trace_best_mat(gen,:)=min(costs20gen');
    else
        vminmat=min(costs20gen');
        vminmat2=trace_best_mat(gen-1,:);
        trace_best_mat(gen,:)=trace_best_mat(gen-1,:);
        mat301=vminmat-vminmat2;
        h301= mat301<0;
        trace_best_mat(gen,h301)=vminmat(h301);
    end
    trace_mean_mat(gen,:)=mean(costs20gen');
    
    waitbar(gen/maxgen,wait_hand);
end
delete(wait_hand);
%% 输出结果

costs=GetCosts(particle);
rep_costs=GetCosts(rep);

程序结果如下:

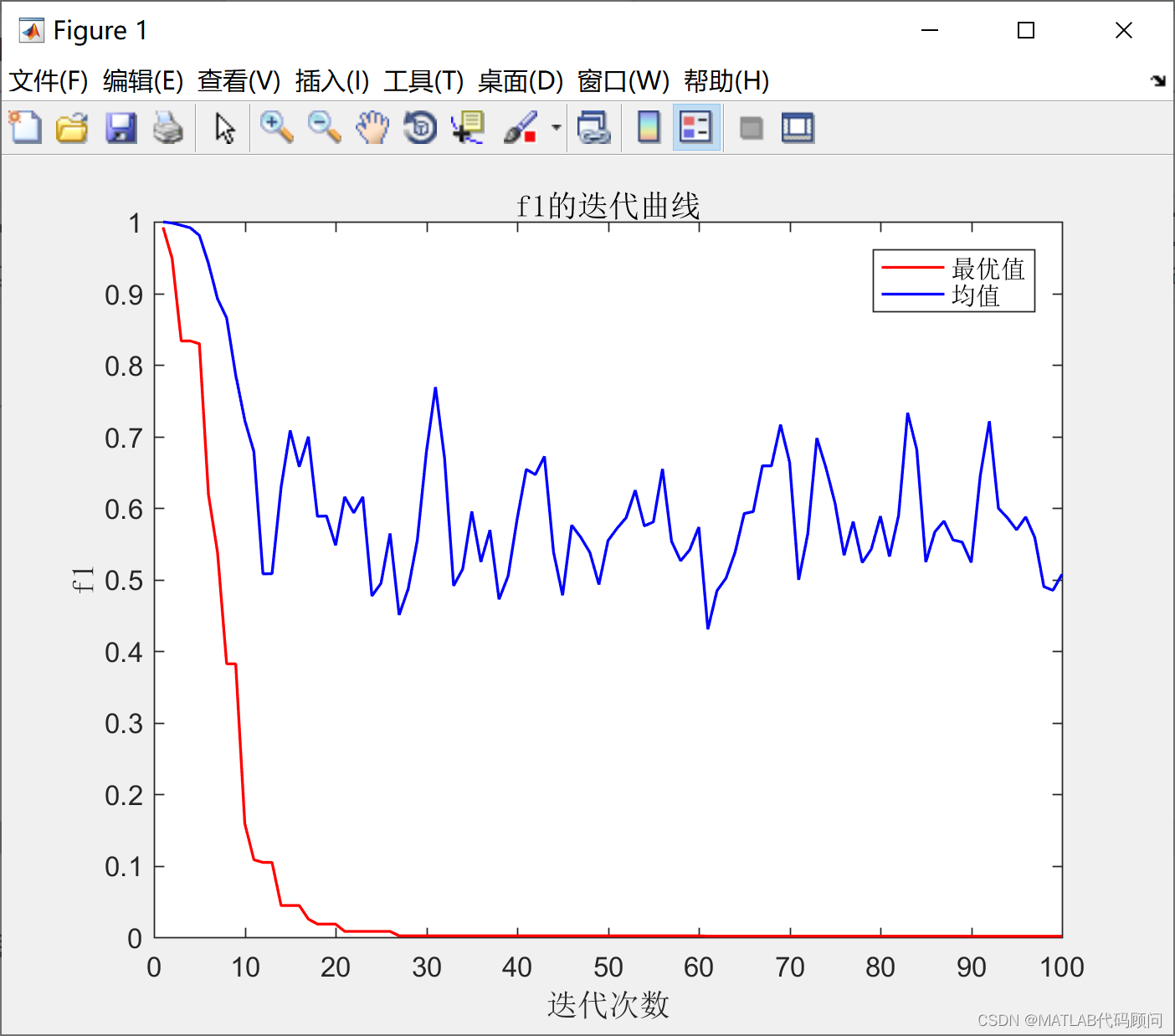
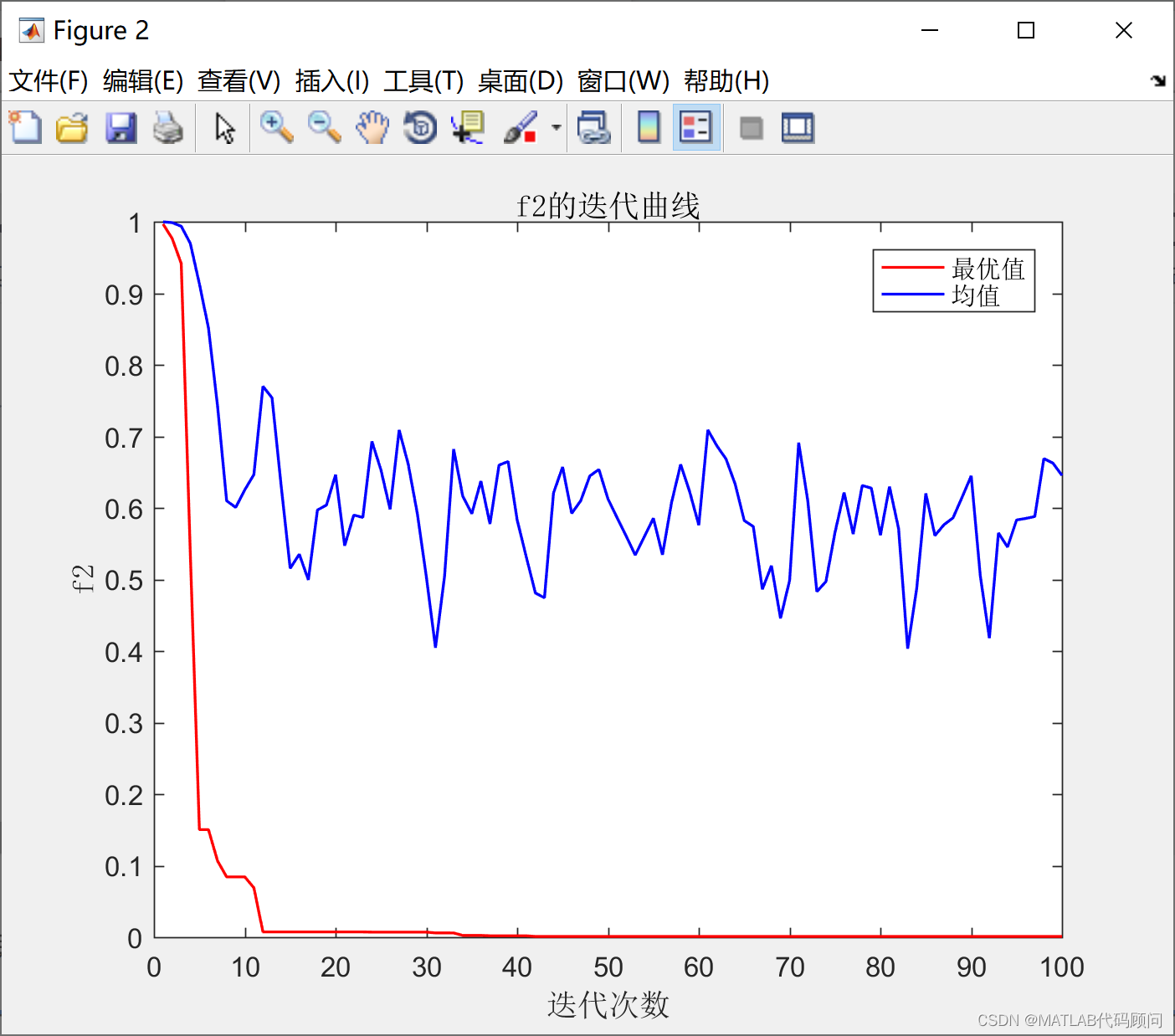
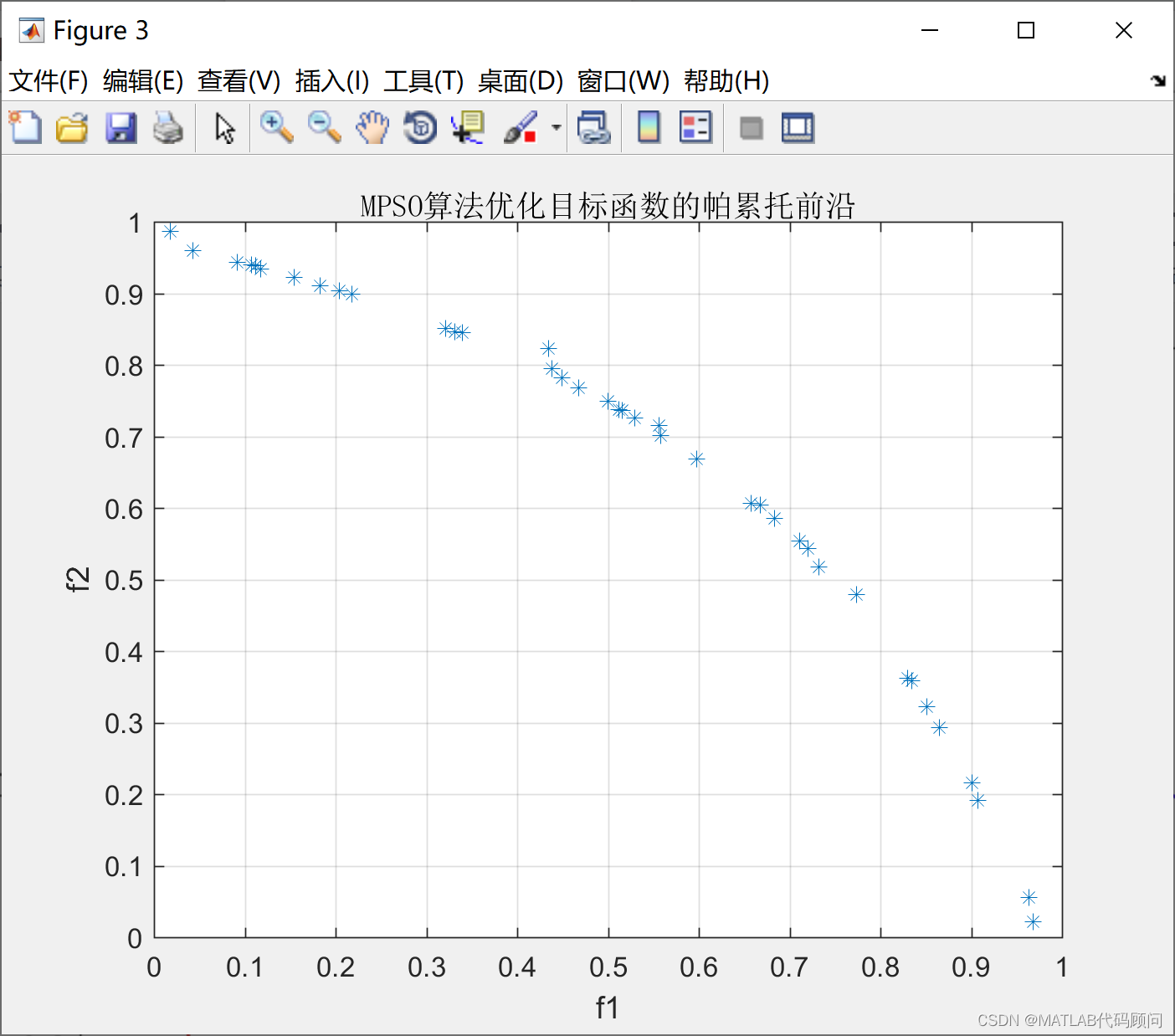
非支配解

paretomat =

      -0.00227284102228413        0.0712188161550257       -0.0163216279512607        0.0223268028879513          0.03405075873276
      -0.00978636830453622         0.170156524714462      -0.00723451433058267        0.0182846191284416        0.0771681625528947
       -0.0176101654801064       -0.0159523975594723      -0.00302200380115747      -0.00849832458300534       -0.0324966912535463
       -0.0419332201068704        0.0746825423487237       -0.0563764778122908       -0.0524243448303948       -0.0229788168721254
       -0.0554839057394384       -0.0989784771813438       -0.0262242055862137        0.0297280418138594     -0.000227264370436242
       -0.0776369060456135       0.00216881072591707       -0.0702366970770566        -0.102944631440041        -0.217642861858831
       -0.0800190754495594        0.0233548532432994        -0.131623720484054       -0.0668297989337753       -0.0185859224973561
       -0.0983626982392394        -0.048037643077243       -0.0692611671055516       -0.0529905948017304       -0.0609328036656522
        -0.105760339390864       -0.0347358884736846       -0.0892373267932827       -0.0545751682409862        0.0407188033358694
        -0.125033787402079        -0.131232202936618        -0.141447071858335        -0.172444620296566        -0.168915834021728
        -0.188399920778113        -0.119726577587646        -0.197052439456695        -0.139812180253481        -0.111490249458453
        -0.189019350743697        -0.144860818694586        -0.192348693379104        -0.179658414736104        -0.141473793690724
        -0.214940684352413        -0.190635157923252        -0.180726899336942        -0.182491821843856        -0.155094670744462
        -0.224468241501541        -0.227546563527362        -0.260585401957969        -0.265522548982672        -0.233156930268307
        -0.259084486658183        -0.195921556728781         -0.29153143335854        -0.231227768412947        -0.176736149549026
        -0.385640587641675        -0.405131975319977        -0.383266402124398        -0.378920251924422        -0.362410294125239
        -0.409708206256663        -0.232258263008486        -0.383276198073093        -0.387622420293001        -0.404531363301304
        0.0266622627949854        0.0199937608076338           0.1020344140958          0.16462373320381         0.335206887783278
         0.029252090464726         0.040560254090536        0.0582231007878223        0.0772952250813304        0.0143580767172984
        0.0523711335156912       0.00916152080864516         0.104635526130941        0.0906404136369576         0.129224191514728
        0.0634041083085849         0.111252555481021        0.0695940580687484        0.0953555138623883         0.124797310908963
        0.0768012955752901        0.0888719244083341         0.076244376622001        0.0273308115915742        0.0763923948232536
        0.0773288220286295        0.0534328982763007          0.12090850599578          0.14178695686211         0.124222179286853
        0.0867509132221776        0.0699405325222435         0.125072236606695        0.0312453154029308        0.0272014961143899
         0.089475649803505        0.0291507738967921        0.0765259423071948        0.0147511082690438        0.0909264711466479
         0.148789021129548         0.161174452260867         0.166142427712131         0.173501657183426         0.196366758068039
         0.151315789987184        0.0688968682546646         0.200197186970212         0.103900972227278        0.0378663627411232
         0.157245805067246          0.15882761519839         0.185975998293083         0.130233154440741         0.188752564844483
          0.16142983238422         0.195238405764086         0.194463073952494          0.16959756042971        0.0874732116423768
          0.22245205415835         0.269650371838859         0.224140784075583         0.246205835016685         0.274971785453224
         0.225154322749349         0.208181362098171         0.249976110858735         0.278973450904965         0.177928756027206
         0.230231006144887         0.235171902542444         0.266234156364099         0.274764469150482         0.174615593267893
         0.236626509303455         0.236665306073303         0.256782832006794         0.296167489627297         0.305962623989305
           0.2477228921018         0.298320394377546         0.289268192825444         0.315014091405021         0.352339375907663
         0.266947443396633         0.324382171096344         0.328350838090562         0.335921585226187         0.235513723671755
         0.278973420929827         0.304392708688683         0.282276552822378         0.289283667760178         0.293413794959001
         0.292384979308659         0.284785782539692         0.339886915529597         0.313743643095613         0.320354289049389
         0.363243384937082         0.379846924117677         0.351984258497255         0.331709064688054         0.347154150516659
         0.518632240891831          0.52936147168219         0.498201970418901         0.474523098342005         0.397491700185792

>> 

 完整代码见: https://download.csdn.net/download/corn1949/89218695

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1621780.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Python小功能实现（链接下载图品并存储到EXCEL中）

Python小功能实现（链接下载图品并存储到EXCEL中）

import os import requests from openpyxl import Workbook from openpyxl.drawing.image import Image from concurrent.futures import ThreadPoolExecutor# 图片链接列表 image_urls ["https://uploads/file/20230205/f85Lpcv8PXrLAdmNUDE1Hh6xqkp0NHi2gSXeqyOb.png&q…
阅读更多...
stm32f103c8t6学习笔记（学习B站up江科大自化协）-UNIX时间戳

stm32f103c8t6学习笔记（学习B站up江科大自化协）-UNIX时间戳

UNIX时间戳 UNIX时间戳最早是在UNIX系统使用的&#xff0c;所以叫做UNIX时间戳&#xff0c;之后很多由UNIX演变而来的系统也继承了UNIX时间戳的规定&#xff0c;目前linux&#xff0c;windows&#xff0c;安卓这些操作系统的底层计时系统都是用UNIX时间戳 时间戳这个计时系统和…
阅读更多...
C++ Qt QMainWindow实现无边框窗口自定义标题栏可拖拽移动拉伸改变窗口大小

C++ Qt QMainWindow实现无边框窗口自定义标题栏可拖拽移动拉伸改变窗口大小

本篇博客介绍C Qt QMainWindow实现无边框窗口&#xff0c;适用于win10/win11系统。 QMainWindow相对于QWidget多了dockedwidget功能&#xff0c;跟多人可能更喜欢用QMainWindow做主窗口&#xff0c;如果不需要dockedwidget功能&#xff0c;QMainWindow与QWidget做主窗口基本无…
阅读更多...
Spring - 4 ( 11000 字 Spring 入门级教程 )

Spring - 4 ( 11000 字 Spring 入门级教程 )

一&#xff1a;Spring IoC&DI 在前⾯的章节中, 我们学习了 Spring Boot 和 Spring MVC 的开发, 可以完成⼀些基本功能的开发了, 但是什么是 Spring 呢? Spring, Spring Boot 和 SpringMVC 又有什么关系呢? 咱们还是带着问题去学习.我们先看什么是Spring 1.1 Spring 是什…
阅读更多...
万兆以太网MAC设计（7）ARP协议报文格式详解以及ARP层模块设计

万兆以太网MAC设计（7）ARP协议报文格式详解以及ARP层模块设计

文章目录 前言&#xff1a;1、ARP协议详解2、ARP工作机制 二、ARP_RX模块设计三、ARP_TX模块设计四、ARP_table模块5、仿真5.1、发送端5.2、接收端5.3、缓存表 总结 前言&#xff1a; 1、ARP协议详解 ARP数据格式&#xff1a; 硬件类型:表示硬件地址的类型。它的值为1表示以太…
阅读更多...
微信小程序使用echarts组件实现饼状统计图功能

微信小程序使用echarts组件实现饼状统计图功能

微信小程序使用echarts组件实现饼状统计图功能 使用echarts实现在微信小程序中统计图的功能&#xff0c;具体的实现步骤思路可进我主页查看我的另一篇博文https://blog.csdn.net/weixin_45465881/article/details/138171153进行查看&#xff0c;本篇文章主要使用echarts组件实…
阅读更多...
javaEE初阶——多线程（九）——JUC常见的类以及线程安全的集合类

javaEE初阶——多线程（九）——JUC常见的类以及线程安全的集合类

T04BF &#x1f44b;专栏: 算法|JAVA|MySQL|C语言 &#x1faf5; 小比特 大梦想 此篇文章与大家分享多线程专题的最后一篇文章:关于JUC常见的类以及线程安全的集合类 如果有不足的或者错误的请您指出! 目录 3.JUC(java.util.concurrent)常见的类3.1Callable接口3.2 RentrantLoc…
阅读更多...
Yolov5 v7.0目标检测——详细记录环境配置、自定义数据处理、模型训练与常用错误解决方法（数据集为河道漂浮物）

Yolov5 v7.0目标检测——详细记录环境配置、自定义数据处理、模型训练与常用错误解决方法（数据集为河道漂浮物）

1. Yolov5 YOLOv5是是YOLO系列的一个延伸&#xff0c;其网络结构共分为&#xff1a;input、backbone、neck和head四个模块&#xff0c;yolov5对yolov4网络的四个部分都进行了修改&#xff0c;并取得了较大的提升&#xff0c;在input端使用了Mosaic数据增强、自适应锚框计算、自…
阅读更多...
鸿蒙云函数调试坑点

鸿蒙云函数调试坑点

如果你要本地调试请使用 const {payload, action} event.body/** 本地调试不需要序列化远程需要序列化 */ // const {payload, action} JSON.parse(event.body) const {payload, action} event.body 注意: 只要修改云函数&#xff0c;必须上传云函数 如果使用 const {pay…
阅读更多...
牛客NC98 判断t1树中是否有与t2树完全相同的子树【simple 深度优先dfs C++/Java/Go/PHP】

牛客NC98 判断t1树中是否有与t2树完全相同的子树【simple 深度优先dfs C++/Java/Go/PHP】

题目 题目链接&#xff1a; https://www.nowcoder.com/practice/4eaccec5ee8f4fe8a4309463b807a542 思路 深度优先搜索暴力匹配 思路和算法这是一种最朴素的方法——深度优先搜索枚举 s 中的每一个节点&#xff0c;判断这个点的子树是否和 t 相等。如何判断一个节点的子树是否…
阅读更多...
HTTP/1.1，HTTP/2.0和HTTP/3.0 各版本协议的详解（2024-04-24）

HTTP/1.1，HTTP/2.0和HTTP/3.0 各版本协议的详解（2024-04-24）

1、HTTP介绍 HTTP 协议有多个版本&#xff0c;目前广泛使用的是 HTTP/1.1 和 HTTP/2&#xff0c;以及正在逐步推广的 HTTP/3。 HTTP/1.1&#xff1a;支持持久连接&#xff0c;允许多个请求/响应通过同一个 TCP 连接传输&#xff0c;减少了建立和关闭连接的消耗。 HTTP/2&#…
阅读更多...
基于STM32和阿里云的智能台灯（STM32+ESP8266+MQTT+阿里云+语音模块）

基于STM32和阿里云的智能台灯（STM32+ESP8266+MQTT+阿里云+语音模块）

一、主要完成功能 1、冷光模式和暖光模式两种灯光 主要支持冷光和暖光模式两种&#xff0c;可以通过语音模块或手机app远程切换冷暖光 2、自动模式和手动模式 主要支持手动模式和自动两种模式&#xff08;app或语音助手切换&#xff09; (1)自动模式&#xff1a;根据环境光照…
阅读更多...
vscode 使用文件模板功能来添加版权信息

vscode 使用文件模板功能来添加版权信息

vscode 新建文件的时候&#xff0c;自动填充作者及版权信息 无需使用插件&#xff0c;操作如下&#xff1a; 选择 “首选项(Preferences)”。在搜索框中输入 “file template” 或者 “文件模板”&#xff0c;然后选择相关的设置项。 {"C_Cpp.clang_format_fallbackSt…
阅读更多...
[lesson58]类模板的概念和意义

[lesson58]类模板的概念和意义

类模板的概念和意义 类模板 一些类主要用于存储和组织数据元素 类中数据组织的方式和数据元素的具体类型无关 如&#xff1a;数组类、链表类、Stack类、Queue类等 C中将模板的思想应用于类,使得类的实现不关注数据元素的具体类型,而只关注类所需要实现的功能。 C中的类模板…
阅读更多...
Docker 开启远程安全访问

Docker 开启远程安全访问

说明 如果你的服务器是公网IP&#xff0c;并且开放了docker的远程访问&#xff0c;如果没有进行保护是非常危险的&#xff0c;任何人都可以向你的docker中推送镜像、运行实例。我曾开放过阿里云服务器中docker的远程访问权限&#xff0c;在没有开启保护的状态下&#xff0c;几…
阅读更多...
企业微信hook接口协议,根据手机号搜索联系人

企业微信hook接口协议,根据手机号搜索联系人

根据手机号搜索联系人 参数名必选类型说明uuid是String每个实例的唯一标识&#xff0c;根据uuid操作具体企业微信 请求示例 {"uuid":"3240fde0-45e2-48c0-90e8-cb098d0ebe43","phoneNumber":"1357xxxx" } 返回示例 {"data&q…
阅读更多...
抖音 小程序 获取手机号 报错 getPhoneNumber:fail auth deny

抖音 小程序 获取手机号 报错 getPhoneNumber:fail auth deny

这是因为 当前小程序没有获取 手机号的 权限 此能力仅支持小程序通过试运营期后可用&#xff0c;默认获取权限&#xff0c;无需申请&#xff1b; https://developer.open-douyin.com/docs/resource/zh-CN/mini-app/develop/guide/open-capabilities/acquire-phone-number-acqu…
阅读更多...
用斐波那契数列感受算法的神奇（21亿耗时0.2毫秒）

用斐波那契数列感受算法的神奇（21亿耗时0.2毫秒）

目录 一、回顾斐波那契数列 二、简单递归方法 &#xff08;一&#xff09;解决思路 &#xff08;二&#xff09;代码展示 &#xff08;三&#xff09;性能分析 三、采用递归HashMap缓存 &#xff08;一&#xff09;解决思路 &#xff08;二&#xff09;代码展示 &…
阅读更多...
深度学习系列65：数字人openHeygen详解

深度学习系列65：数字人openHeygen详解

1. 主流程分析 从inference.py函数进入&#xff0c;主要流程包括&#xff1a; 1&#xff09; 使用cv2获取视频中所有帧的列表&#xff0c;如下&#xff1a; 2&#xff09;定义Croper。核心代码为69行&#xff1a;full_frames_RGB, crop, quad croper.crop(full_frames_RGB)。…
阅读更多...
公开课学习——基于索引B+树精准建立高性能索引

公开课学习——基于索引B+树精准建立高性能索引

文章目录 遇到慢查询怎么办&#xff1f;—— 创建索引联合索引的底层的数据存储结构长什么样&#xff1f; mysql脑图 阿里开发手册 遇到慢查询怎么办&#xff1f;—— 创建索引 不用索引的话一个一个找太慢了&#xff0c;用索引就快的多。 假如使用树这样的结构建立索引&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023