如下是题目的简单描述:
给你一棵二叉树的根节点 root ,二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟,感染 将会从值为 start 的节点开始爆发。
每分钟,如果节点满足以下全部条件,就会被感染:
节点此前还没有感染。
节点与一个已感染节点相邻。
返回感染整棵树需要的分钟数。
然后是官方给的数据的例子:
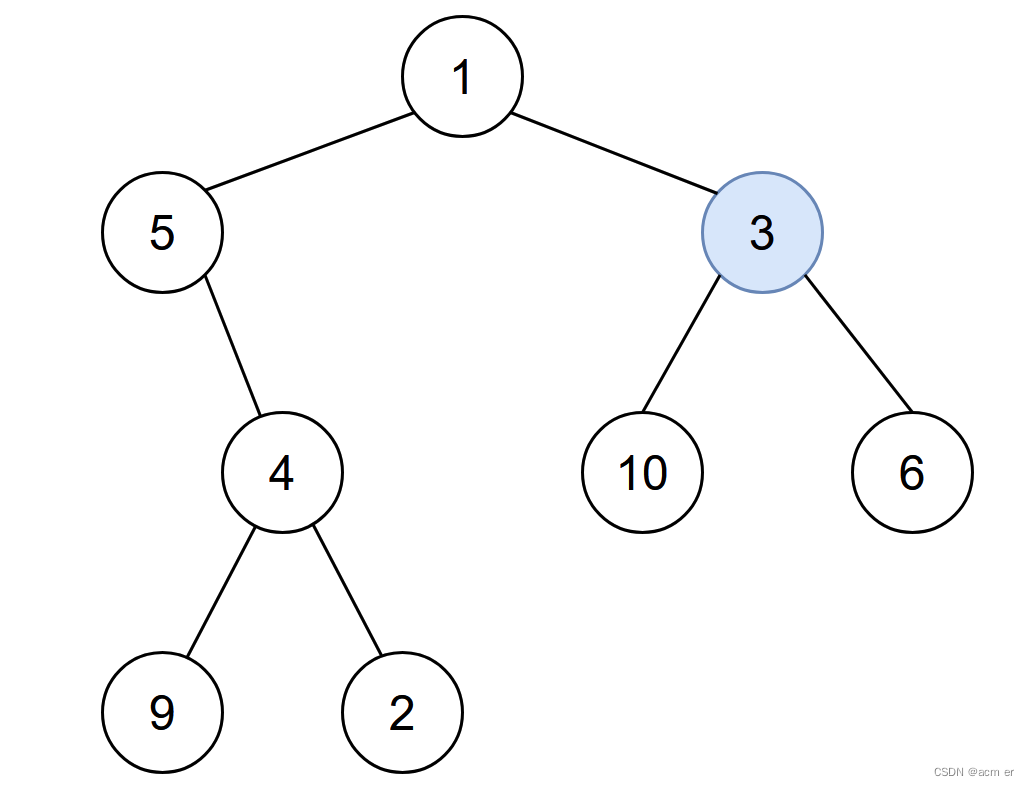
输入:root = [1,5,3,null,4,10,6,9,2], start = 3
输出:4
解释:节点按以下过程被感染:
- 第 0 分钟:节点 3
- 第 1 分钟:节点 1、10、6
- 第 2 分钟:节点5
- 第 3 分钟:节点 4
- 第 4 分钟:节点 9 和 2
感染整棵树需要 4 分钟,所以返回 4 。
这题的思想类似于求树的直径,这个题目给了我们一个start作为我们的出发点,那么我们考虑一下,从这个出发点往两侧延伸最长的直径应该就是我们要找的最大的距离,那么这里考虑一下这个直径的问题怎么理解?
考虑如下这张图:
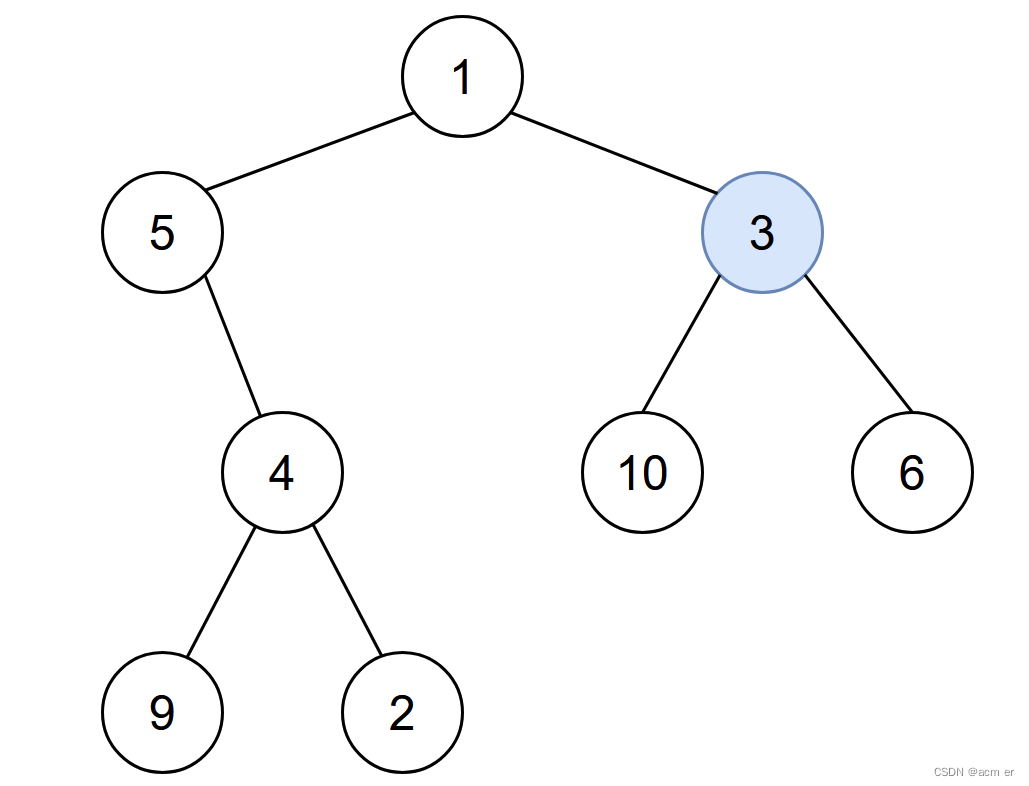
这张图,我门假设从3这个节点开始哈,那么我们可以看到3有三个延伸方向:
3-10 3-6 以及上面那个 3-1 那么针对这几条路呢,我们只需要找出其中最长的那条路 也就是3作为端点的最长路径延伸 可以成为直径,显然这个图来说:
3-1-5-4-(2,9)就是最长的路径,也就是我们最终需要求得的最长扩散时间。
具体实现算法如下:
这里我们需要先声明一下,因为需要记录当前子树是否包含当前的start点,我们需要一个额外的返回值作为判断 也就是(dep,bool),所以我们返回值用pair,具体实现细节以及相关逻辑都在代码里面注释了,看代码更好理解一些:
class Solution {
public:
int ans = 0, start;
pair<int, int> dfs(TreeNode* node){
if(node == nullptr){
return {0, false};
}
auto [l_len, l_found] = dfs(node->left);
auto [r_len, r_found] = dfs(node->right);
if(node->val == start){
ans = max(l_len, r_len);//同时要更新一下这个ans,因为有可能最大的结果存在于start的另一端,这里不加1的原因是 是在返回start之前做的,那么其实计算的长度本身就是路径的长度,也就是回溯到start之前所经过的路径长度 这个大家要对递归的思想理解好哈
return {1, true};//这里这个1很关键 一定要1这个start为端点进行延伸 求最大的直径 所以到达start那么就从1进行返回 他的所有节点都忽略不计
}
if(l_found || r_found){
ans = max(ans, l_len + r_len);//合并直径进行更新,这里不加1的原因是因为刚才遇到start的时候已经返回1了,那么针对比如他的上一级节点,到他的距离就是1,我们直接取l_len后者r_len本身的值就可以了。
return {(l_found ? l_len : r_len) + 1,true};//这里的话需要注意的就是 如果在左侧找到了,我们要保证start作为我们直径的端点 所以要返回l_len + 1,而且为true,这里+1的目的是因为我们需要更新合法的距离
}
return {max(l_len, r_len) + 1, false};//这个就是左右都没有,只需要正常返回高度即可
}
int amountOfTime(TreeNode* root, int start) {
this->start = start;
dfs(root);
return ans;
}
};