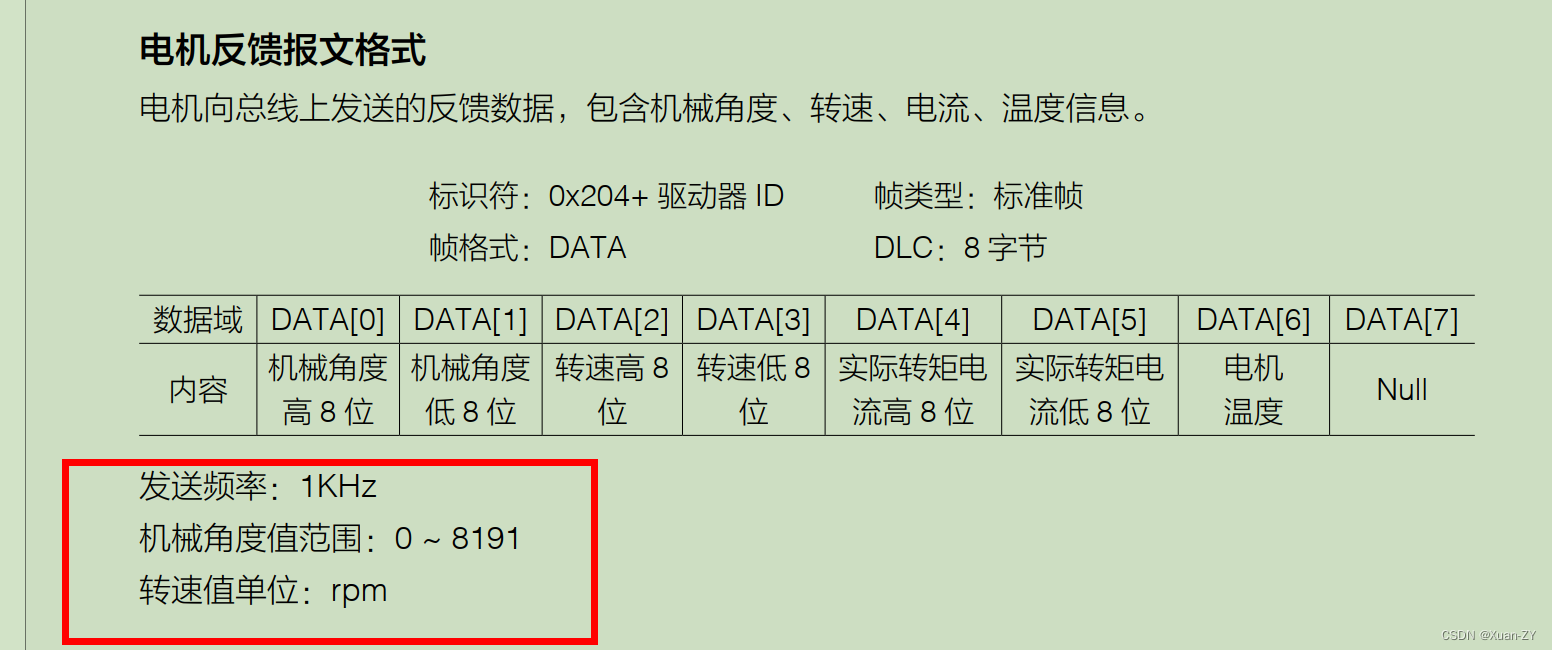
矩阵相关题型
Leetcode 48. 旋转图像【中等】
题意理解:
将一个矩阵顺时针旋转90度,返回旋转后的矩阵。
要求: 在原地修改,不借助额外的空间
如果可以使用辅助数组来实现转置,则有
matrix_new[i][j]=matrix[j][row-i-1];
解题思路:
(1) 四数循环:
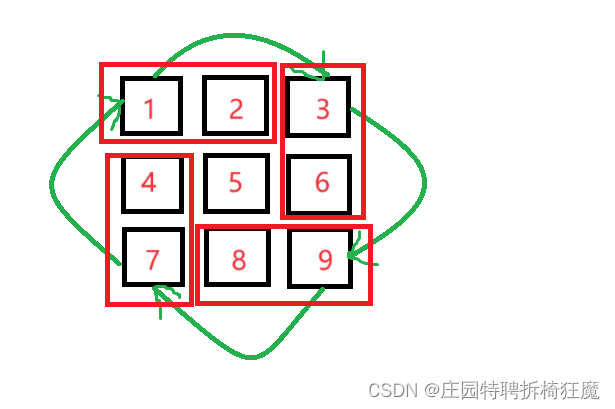
将其一层一层的进行转置
首先看最外面的一层,将其分为红色方框中的四部分
从第一个红色方框开始: 第一个位置(0,0)将转置到(0,2)的位置上
原本(0,2)的位置上的数转置到(2,2),
原来(2,2)上的数转置到(2,0)
原来(2,0)的位置转置到(0,0)
即: (0,0)->(0,2)->(2,2)->(2,0)->(0,2)->(0,0)
坐标变化为: (i,j)->(j,row-i-1) 变换四次
完成一个红色框的所有元素的变换,则完成了一层数据的转置
如何进入下一层呢?
i++,j++即可,重复上述操作。
何时跳出循环:
当且仅当,i,j指向中心元素时,跳出循环,如下图中: i=3/2=1 时,走到矩阵核心,不需要继续转置
能不能理解更简单一些呢?
对于四数循环的while可以从循环中展开:即实现四数互换
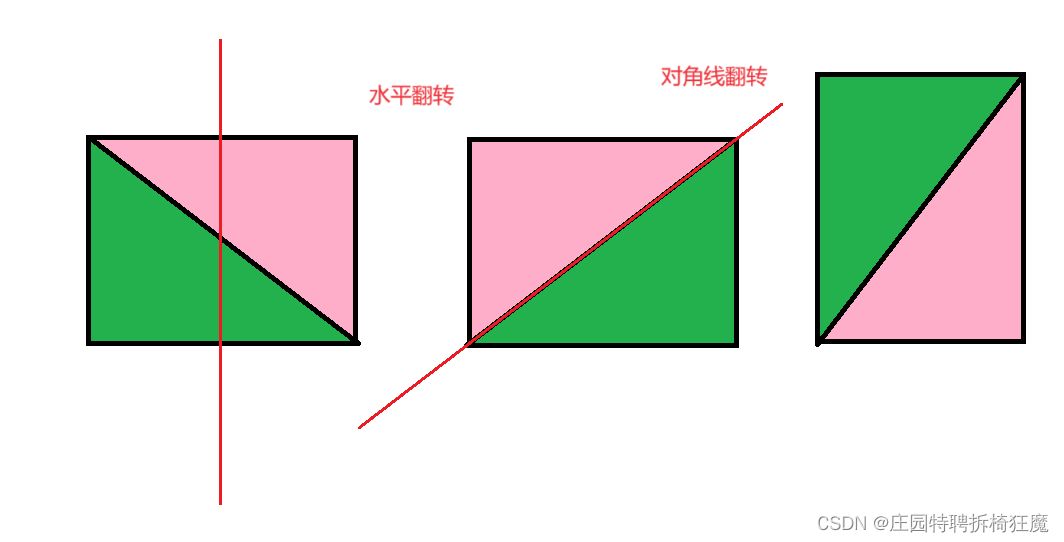
思路二:反转替代转置
顺时针转置90度=水平+对角线
水平翻转: new_i,new_j=row-i-1,j
对角线反转: new_i,new_j=j,i
1.解题【四数循环】
class Solution {
public void rotate(int[][] matrix) {
//使用坐标变换的逻辑,实现旋转
int row=matrix.length,col=matrix[0].length;
int cur_i=0,cur_j=0;
int curVal=matrix[cur_i][cur_j];
while(cur_i!=row/2){
for(int j=cur_i;j<row-cur_i-1;j++){
cur_j=j;
curVal=matrix[cur_i][cur_j];
int count=4;
while(count-->0){
int next_i=cur_j;
int next_j=row-cur_i-1;
int nextVal=matrix[next_i][next_j];
matrix[next_i][next_j]=curVal;
cur_i=next_i;
cur_j=next_j;
curVal=nextVal;
}
}
cur_i++;
}
}
}改进:可以将四数循环的while展开写:
class Solution {
public void rotate(int[][] matrix) {
//使用坐标变换的逻辑,实现旋转
int row=matrix.length,col=matrix[0].length;
int cur_i=0;
while(cur_i!=row/2){
for(int cur_j=cur_i;cur_j<row-cur_i-1;cur_j++){
int temp=matrix[cur_i][cur_j];
matrix[cur_i][cur_j]=matrix[row-cur_j-1][cur_i];
matrix[row-cur_j-1][cur_i]=matrix[row-cur_i-1][row-cur_j-1];
matrix[row-cur_i-1][row-cur_j-1]=matrix[cur_j][row-cur_i-1];
matrix[cur_j][row-cur_i-1]=temp;
System.out.println( matrix[cur_i][cur_j]+" "+matrix[row-cur_i-1][cur_j]+" "+matrix[row-cur_i-1][row-cur_j-1]+" "+matrix[cur_i][row-cur_j-1]);
}
cur_i++;
}
}
}1.翻转替代转置【水平翻转+对角线翻转】
class Solution {
public void rotate(int[][] matrix) {
//使用坐标变换的逻辑,实现旋转
int row=matrix.length,col=matrix[0].length;
//水平翻转
for(int i=0;i<row/2;i++){
for(int j=0;j<col;j++){
int temp=matrix[i][j];
matrix[i][j]=matrix[row-i-1][j];
matrix[row-i-1][j]=temp;
}
}
//对角线翻转
for(int i=0;i<row;i++){
for(int j=0;j<i;j++){
int temp=matrix[i][j];
matrix[i][j]=matrix[j][i];
matrix[j][i]=temp;
}
}
}
}2.复杂度分析
时间复杂度:O(n^2) while(n/2)+for循环+4次while循环的时间损耗
空间复杂度:O(1) 原地转置的空间损耗
Leetcode 240. 搜索二维矩阵 II【中等】
题意理解:
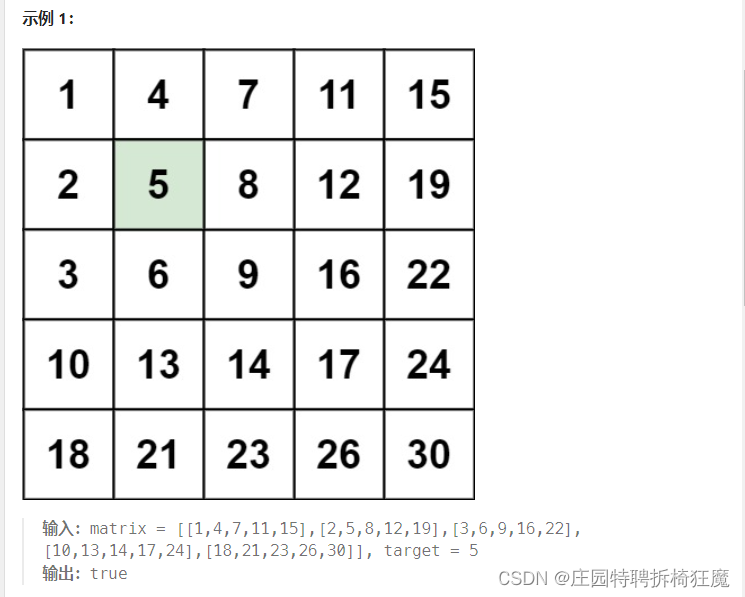
这个矩阵是有顺序的,左到右升序,上到下升序
要求找到执行的元素,找到为true,否则为false
解题思路:
1.逐个对比:双for循环
2.由于每行都是升序,可以对于每行进行二分排序
3.对角线查找:每行都是顺序升序的,每列也是升序的
从右上角到左下角,比当前值大往左,比当前值小往下
上下维度控制变大,左右维度控制变小
1.解题【双for循环】
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int row=matrix.length,col=matrix[0].length;
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
if(matrix[i][j]==target) return true;
}
}
return false;
}
}1.解题:【遍历行二分查】
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int row=matrix.length,col=matrix[0].length;
for(int i=0;i<row;i++){
//对每行进行二分查找
int low=0,high=col-1;
while(low<=high){
int mid=(high-low)/2+low;
int midNum=matrix[i][mid];
if(midNum==target) return true;
else if(midNum>target){
high=mid-1;
}else{
low=mid+1;
}
}
}
return false;
}
}1.解题:【对角线查找】
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int row=matrix.length,col=matrix[0].length;
int i=0,j=col-1;
//从右上角往左下角找,==返回>往左,<往下
while(x<row&&y>=0){
if(matrix[i][j]==target){
return true;
}else if(matrix[i][j]>target){
j--;
}else if(matrix[i][j]<target){
i++;
}
}
return false;
}
}2.复杂度分析
思路一:
时间复杂度:O(n^2) 双for的时间损耗
空间复杂度:O(1) 变量的空间损耗
思路二:
时间复杂度:O(nlogn) for+二分的时间损耗
空间复杂度:O(1) 变量的空间损耗
思路一:
时间复杂度:O(n) 双for的时间损耗
空间复杂度:O(1) 变量的空间损耗