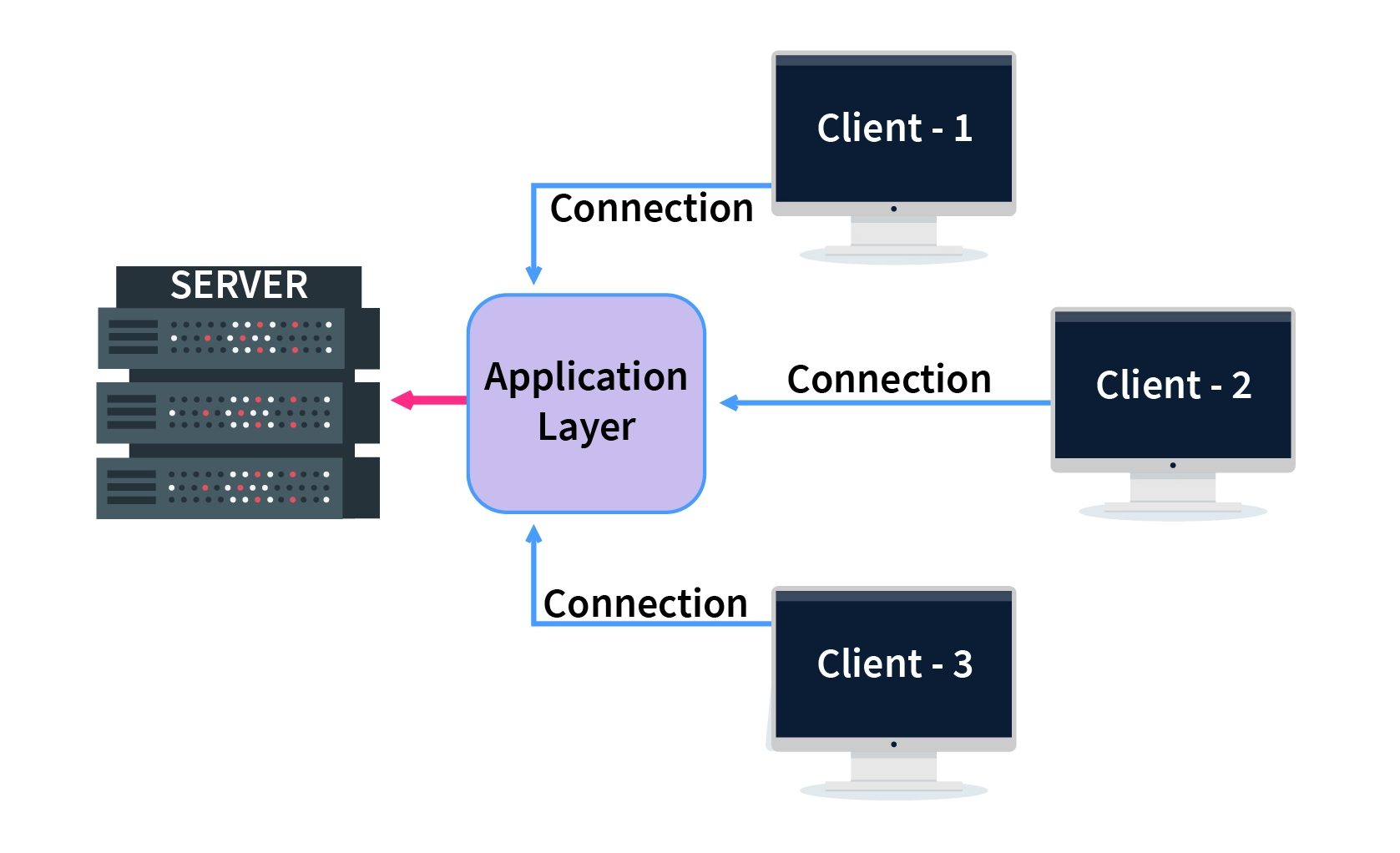
一、一些补充的概念

1. 如果具有n个结点的图中是一个环，则会有n个不同的生成树，每个生成树有n-1条边

2. 连通、连通图、连通分量：路径，无向图 ，极大连通子图为连通分量，边数小于n-1，则图必为非连通图。

3. 线性表可以是空表，一个元素也没有;树可以是空树，一个结点也没有但图不可以一个顶点也没有，所谓空图是指图中的边数为零。图的顶点集合一定非空,而边集合可以为空。

4. 顶点的度是指与顶点相关联的边数，对于有向图，还要区分出度和入度

5. 在有向图中的边是有向的，<x, y>与<y, x>是不同的两条边。在无向图中的边是无向的, (x.y)与(y,x)是同一条边。

6. 顶点之间的路径用一个顶点序列标识。无权图的路径长度用所经过边的条数标识，带权图的路径长度用所经过边上的权值之和标识。

7. 连通性一般指的是在无向图中的性质，而在有向图情形要考虑的是强连通性。

8. 图的生成树是由顶点和顶点之间关系组成的连通图。有n个顶点,必有n-1
   条边将它们连通。要注意的是,这种生成树不能是空树。

9. 从非强连通的有向图和非连通的无向图通过遍历得到的是生成森林。

10. 不像线性表，元素之间有前趋后继关系：也不像树、结点之间有父子分层关系：在图中各个顶点之间的地位是平等的因此可以按照需要，对图中顶点重新编号。

11. 稀疏图的边数远少于图的顶点数的平方，稠密图则不是

12. 在无向图中，顶点v被称作一个关节点，当且仅当删除v以及依附于v的所有边之后，图将被分割成至少两个连通分量。

13. 对一个图G进行遍历可以得到不同的遍历序列，那么导致得到的遍历序列不唯一的因素有哪些？
    导致遍历序列不唯一的因素有：
    (1) 由于途中每个顶点可能有多个邻接点，使得遍历序列不唯一
    (2) 遍历的出发点不同，遍历序列也不同
    (3) 如果采用邻接表存储，由于各边链入顺序任意，同一个图的存储表示不唯一，遍历结果也可能不唯一。

14. 图的深度优先搜索是一个递归的过程，而广度优先搜索为何是非递归的过程？
    广度优先搜索的过程是从图的某个顶点出发，围绕该顶点一圈一圈访问图中所有顶点的过程，与树的逐层访问类似，因此他不用递归实现，只需利用队列迭代式实现。

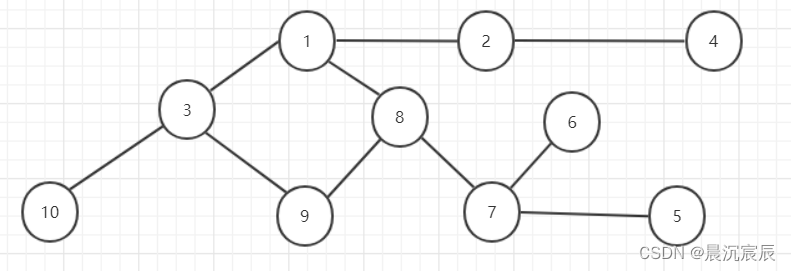
15. (1)画出上图以顶点1为根的DFS生成树
    (2)如果有关节点，请找出所有的关节点 1，2，3，7，8
    (3)如果想把该连通图变成双连通图，需要消除所有关节点，那么至少在图中加几条边？如何加？
    至少三条边。一条边是(9, 10),一条边是(4, 6), 一条边是(5, 6)
    

16. 构造最小生成树的三条准则：
    （1）有n个顶点的生成树仅有n-1条边
    （2）不能使用产生回路的边。
    （3） 树的总代价最小。

17. 构造最小生成树的方法：prim 和 kruskal

18. 建立最小生成树的要点
    如果连通带权图中各边上的权值互不相等,构造出来的最小生成树是唯一的;如果存在权值相等的边,若采用邻接表存储，由于选择边的次序不同，构造出来的最小生成树是不唯一的,不过它们总的权值之和应相同。若采用邻接矩阵存储,则结果是唯一的。

19. 若带权连通图中有权值为负的边，使用prim或kruskal仍可构造最小生成树。

20. 在什么情况下.对同一连通网络使用Prim算法与Kruskal算法，得到的最小生成树会不同?
    答：当带权连通图(连通网络)中具有相同较小权值的几条边形成回路时，两个算法由于选边的次序不同:可能生成不同的最小生成树。

21. 对于一个连通网络,具有最小权值的顶点是否一定在最小生成树上?具有次小权直、第三小权值的顶点情况又如何?
    答：如果连通网络各条边上的权值互不相同，具有最小或次小权值的边一定在最小生成树上，具有第三小权值的边就不-定，要看它是否与具有最小和次小权值的顶点构成回路。如果连通网络中有多条具有最小或次小权值的边，且构成了回路，有部分具有最小或次小权值的边可能不在最小生成树上，具有第三小权值的边更不一定了。

22. 求单源最短路径的Dijkstra算法

23. 求各个顶点之间最短路径的Floyd算法（如果不会Floyd，也可以把每一个顶点作为源点，使用Dijstra算法）

24. Dijkstra算法的时间复杂度为O(n2),因为图中几乎所有顶点都要做计算
    Floyd算法的时间复杂度为O(n3)

25. 简述Dijkstra算法与Prim算法的异同？
    答： Dijkstra算法是求带权图单源最短路径的算法,Prim算法是求带权图最小生成树的算法，它们的用途不同。Dijkstra算法和Prim算法同属贪心法，它们的工作过程相同，都是逐步递增求解的过程。不同之处在于Dijkstra算法每次比较的是源点到各顶点的路径长度,而Prim算法每次比较的是边上的权值。此外,Dijkstra算法的限制是边上的权值非负，而Prim算法没有这个限制。

26. 图中的顶点表示村庄，有向边表示交通路线。若要建立一家医院，试问在哪一个村庄能使各村庄总体上的交通代价最小。

27. 拓扑排序操作题要掌握

28. 关键路径的简单算法和正规算法都要求掌握

29. 什么是拓扑排序？它是针对何种结构的？
    答：把一个偏序(有向)图转换为全序图的过程叫做拓扑排序。排序结果把图的所有顶点排在一个拓扑有序的序列中。该序列不但保留了原偏序图中所有顶点的优先关系，而且给原先没有关系的顶点之间也赋予了优先关系。拓扑排序针对AOV网络(工程计划网络)

30. 对任何AOV网络进行拓扑排序，结果不唯一的影响因素有哪些？
    影响因素有三：
    (1) 图结构本身的影响。如果图有多个无前趋的顶点，或输出一个顶点并删除该顶点发出的有向边后，出现多个入度为零的顶点，就会产生多个拓扑有序序列。
    (2) 图存储结构的影响。采用邻接矩阵存储图，处理出边的次序是唯一的；采用邻接表存储图，处理出边的次序是不唯一的。
    (3) 算法所用辅助结构的影响。入度为零的结点可以用栈来组织，也可以用队列来组织，自然算法生成的拓扑有序序列也会不同。

31. 拓扑排序的一个重要应用是判断有向图是否有环。如何判断？
    每次寻找一个入度为0的顶点，输出它并把所有它发出的边删去，作为这些边的终顶点的入度减一，如此重复，找到所有的顶点全部输出，说明图中没有环；如果过程中还有顶点未输出，但没有入度为0的顶点了，说明图中有环。

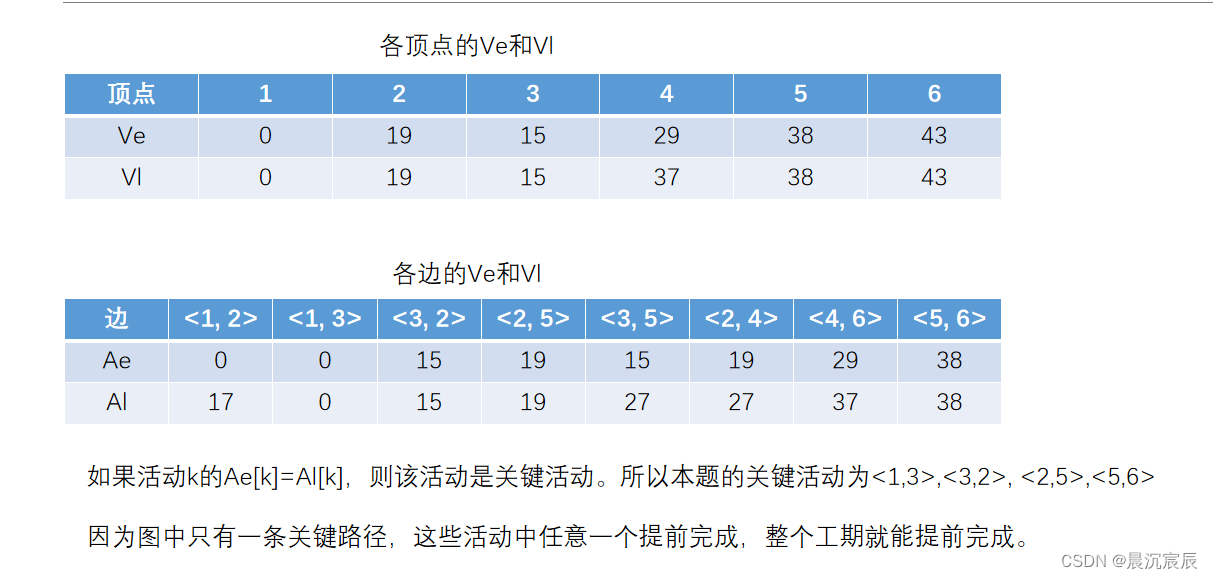
32. (1) 这个工程最早可能什么时间结束？
    (2) 确定哪些是关键活动。画出由所有关键活动构成的图，指出哪些活动加速可使整个工程提前完成。
    

二、基础算法

1. 深度遍历

2. 广度遍历

（1） 基础算法

（2）力扣练习题

1） 题目一

1. 题目
被包围的区域
给你一个 m x n 的矩阵 board ，由若干字符 ‘X’ 和 ‘O’ ，找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

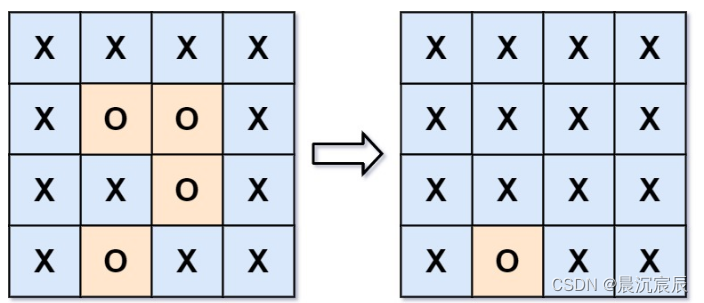
2. 思路：（1）本题要求将所有被字母 X 包围的字母 O都变为字母 X ，但很难判断哪些 O 是被包围的，哪些 O 不是被包围的。
（2）注意到题目解释中提到：任何边界上的 O 都不会被填充为 X。 我们可以想到，所有的不被包围的 O 都直接或间接与边界上的 O 相连。我们可以利用这个性质判断 O 是否在边界上，具体地说：
① 对于每一个边界上的 O，我们以它为起点，标记所有与它直接或间接相连的字母 O；
② 最后我们遍历这个矩阵，对于每一个字母：
a. 如果该字母被标记过，则该字母为没有被字母 X 包围的字母 O，我们将其还原为字母 O；
b. 如果该字母没有被标记过，则该字母为被字母 X 包围的字母 O，我们将其修改为字母 X。
3. 解题：
方法一：深度优先搜索
我们可以使用深度优先搜索实现标记操作。在下面的代码中，我们把标记过的字母 O 修改为字母 A。

class Solution {
public:
    int n, m;
   //利用深度遍历，判断上下左右有没有连接的0，并且将它标记为A
    void dfs(vector<vector<char>>& board, int x, int y) {
        if (x < 0 || x >= n || y < 0 || y >= m || board[x][y] != 'O') {
            return;
        }
        board[x][y] = 'A';
        dfs(board, x + 1, y);
        dfs(board, x - 1, y);
        dfs(board, x, y + 1);
        dfs(board, x, y - 1);
    }

    void solve(vector<vector<char>>& board) {
        n = board.size();
        if (n == 0) {
            return;
        }
        m = board[0].size();
        for (int i = 0; i < n; i++) {
            dfs(board, i, 0);//遍历第一列
            dfs(board, i, m - 1);//遍历最后一列
        }
        for (int i = 1; i < m - 1; i++) {
            dfs(board, 0, i);//遍历第一行
            dfs(board, n - 1, i);//遍历最后一行
        }
        //以上步骤就是利用深度遍历，将与边界的0相连的0都变成A，此时，剩余的0都是被x包围的。
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }//for2 
        }//for1 此时将所有未标记的0变为x
    }
};

复杂度分析
（1）时间复杂度：O(n \times m)O(n×m)，其中 nn 和 mm 分别为矩阵的行数和列数。深度优先搜索过程中，每一个点至多只会被标记一次。
（2）空间复杂度：O(n \times m)O(n×m)，其中 nn 和 mm 分别为矩阵的行数和列数。主要为深度优先搜索的栈的开销。
方法一：广度优先搜索

class Solution {
public:
    const int dx[4] = {1, -1, 0, 0};
    const int dy[4] = {0, 0, 1, -1};

    void solve(vector<vector<char>>& board) {
        int n = board.size();
        if (n == 0) {
            return;
        }
        int m = board[0].size();
        queue<pair<int, int>> que;
        for (int i = 0; i < n; i++) {
            if (board[i][0] == 'O') {
                que.emplace(i, 0);
                board[i][0] = 'A';
            }
            if (board[i][m - 1] == 'O') {
                que.emplace(i, m - 1);
                board[i][m - 1] = 'A';
            }
        }
        for (int i = 1; i < m - 1; i++) {
            if (board[0][i] == 'O') {
                que.emplace(0, i);
                board[0][i] = 'A';
            }
            if (board[n - 1][i] == 'O') {
                que.emplace(n - 1, i);
                board[n - 1][i] = 'A';
            }
        }
        while (!que.empty()) {
            int x = que.front().first, y = que.front().second;
            que.pop();
            for (int i = 0; i < 4; i++) {
                int mx = x + dx[i], my = y + dy[i];
                if (mx < 0 || my < 0 || mx >= n || my >= m || board[mx][my] != 'O') {
                    continue;
                }
                que.emplace(mx, my);
                board[mx][my] = 'A';
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }
    }
};

复杂度分析
（1）时间复杂度：O(n \times m)O(n×m)，其中 nn 和 mm 分别为矩阵的行数和列数。广度优先搜索过程中，每一个点至多只会被标记一次。
（2）空间复杂度：O(n \times m)O(n×m)，其中 nn 和 mm 分别为矩阵的行数和列数。主要为广度优先搜索的队列的开销。

2） 题目二

最小基因变化
基因序列可以表示为一条由 8 个字符组成的字符串，其中每个字符都是 ‘A’、‘C’、‘G’ 和 ‘T’ 之一。
假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。
例如，“AACCGGTT” --> “AACCGGTA” 就是一次基因变化。
另有一个基因库 bank 记录了所有有效的基因变化，只有基因库中的基因才是有效的基因序列。（变化后的基因必须位于基因库 bank 中）
给你两个基因序列 start 和 end ，以及一个基因库 bank ，请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化，返回 -1 。
注意：起始基因序列 start 默认是有效的，但是它并不一定会出现在基因库中。
示例 1：
输入：start = “AACCGGTT”, end = “AACCGGTA”, bank = [“AACCGGTA”]
输出：1
示例 2：
输入：start = “AACCGGTT”, end = “AAACGGTA”, bank = [“AACCGGTA”,“AACCGCTA”,“AAACGGTA”]
输出：2
1. 思路与算法
（1）经过分析可知，题目要求将一个基因序列 AA 变化至另一个基因序列 BB，需要满足一下条件：

• 序列 AA 与 序列 BB 之间只有一个字符不同；
• 变化字符只能从{‘A’, ‘C’, ‘G’, ‘T’ }中进行选择；
• 变换后的序列 BB 一定要在字符串数组 bank 中。

（2）根据以上变换规则，我们可以进行尝试所有合法的基因变化，并找到最小的变换次数即可。步骤如下：

• 如果start 与 end 相等，此时直接返回 0；如果最终的基因序列不在bank 中，则此时按照题意要求，无法生成，直接返回 -1；
• 首先我们将可能变换的基因 s 从队列中取出，按照上述的变换规则，尝试所有可能的变化后的基因，比如一个 AACCGGTA，我们依次尝试改变基因 ss 的一个字符，并尝试所有可能的基因变化序列 s0,s1,s2 ,⋯,si,⋯,s​变化一次最多可能会生成 3×8=24 种不同的基因序列。
• 我们需要检测当前生成的基因序列的合法性 ，首先利用哈希表检测 si是否在数组bank 中，如果是则认为该基因合法，否则改变化非法直接丢弃；其次我们还需要用哈希表记录已经遍历过的基因序列，如果该基因序列已经遍历过，则此时直接跳过；如果合法且未遍历过的基因序列，则我们将其加入到队列中。
• 如果当前变换后的基因序列与end相等，则此时我们直接返回最小的变化次数即可；如果队列中所有的元素都已经遍历完成还无法变成end，则此时无法实现目标变化，返回 -1。
  -
  复杂度分析
  （1）时间复杂度：O(c×n×m)，其中 nn 为基因序列的长度，m 为数组 bank 的长度。对于队列中的每个合法的基因序列每次都需要计算c×n 种变化，在这里 C = 4；队列中最多有m 个元素，因此时间复杂度为 O(c×n×m)。
  （2）空间复杂度：O(n×m)，其中 n为基因序列的长度，m 为数组 bank 的长度。合法性的哈希表中一共存有 m 个元素，队列中最多有 m 个元素，每个元素的空间为 O(n)；队列中最多有 m 个元素，每个元素的空间为 O(n)，因此空间复杂度为 O(n×m)。

3. 拓扑排序

（1）基础算法

Status TopologicalSort(ALGraph G, int topo[]) {
    //有向图 G 采用邻接表存储结构
    //若 G 无回路，则生成 G 的一个拓扑排序 topo[]并返回 OK，否则 ERROR
    FindInDegree(G, indegree);//求出各结点的入度存入数组 indegree 中
    SqStack S;
    InitStack(S);//初始化栈
    for (int i = 0; i < G.vexnum; i++) {
       if (!indegree[i]) Push(S, i);//入度为 0 者进栈
     }
    int m = 0;//对输出顶点计数 u，初始为 0
    while (!StackEmpty(S)) {
       int i = 0;
       Pop(S, i);//将栈顶顶点 vi 出栈
       topo[m] = i;//将 vi 保存在拓扑序列数组 topo 中
       ++m;//对输出顶点计数
       ArcNode* p = new ArcNode;
       p = G.vertices[i].firstarc;//p 指向 vi 的第一个邻接点
      while (p != NULL) {
         int k = p->adjvex;//vk 为 vi 的邻接点
         --indegree[k];//vi 的每个邻接点的入度减一
          if (indegree[k] == 0) Push(S, k);//若入度减为 0，则入栈
          p = p->nextarc;//p 指向顶点 vi 下一个邻接结点
        }
     }
    if (m < G.vexnum) return ERROR;//该有向图有回路
         else return OK;
}

（2）力扣练习题

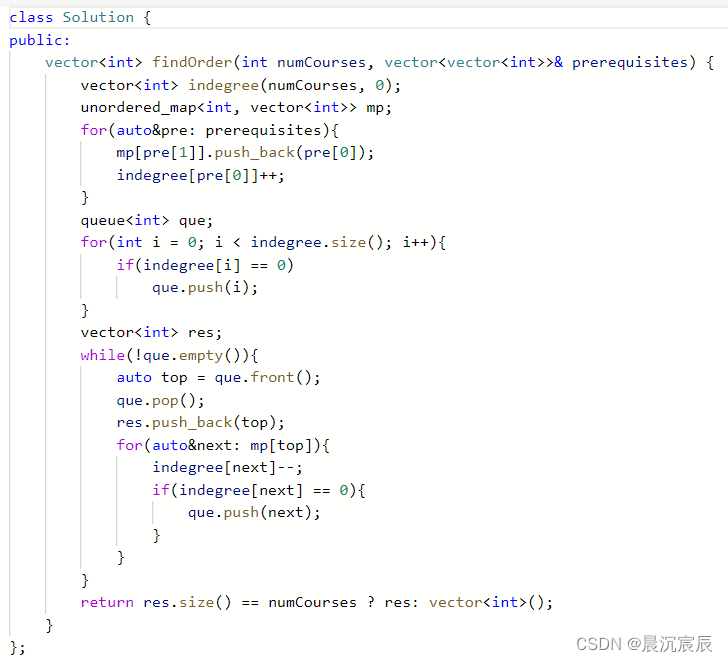
课程2
现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须先选修 bi 。
例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一空数组 。

输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3] 解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2
都应该排在课程 0 之后。 因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

三、新增考点—Bellman-Ford 单源最短路径算法

1. 算法描述：
   （1）对于带权有向图 G = (V, E)，Dijkstra 算法要求图 G 中边的权值均为非负，而 Bellman-Ford 算法能适应一般的情况（即存在负权边的情况）。一个实现的很好的 Dijkstra 算法比 Bellman-Ford 算法的运行时间要低。
   （2）Bellman-Ford 算法采用动态规划（Dynamic Programming）进行设计，实现的时间复杂度为 O(V*E)，其中 V 为顶点数量，E 为边的数量。Dijkstra 算法采用贪心算法（Greedy Algorithm）范式进行设计，普通实现的时间复杂度为 O(V2)，若基于 Fibonacci heap 的最小优先队列实现版本则时间复杂度为 O(E + VlogV)。
2. 算法思路
   1）创建源顶点 v 到图中所有顶点的距离的集合 distSet，为图中的所有顶点指定一个距离值，初始均为 Infinite，源顶点距离为 0；
   2） 计算最短路径，执行 V - 1 次遍历；
   对于图中的每条边：如果起点 u 的距离 d 加上边的权值 w 小于终点 v 的距离 d，则更新终点 v 的距离值 d；
   3）检测图中是否有负权边形成了环，遍历图中的所有边，计算 u 至 v 的距离，如果对于 v 存在更小的距离，则说明存在环；
3. Bellman-Ford 算法的运行时间为 O(V*E)，因为第 2 行的初始化占用了 Θ(V)，第 3-4 行对边进行了 V - 1 趟操作，每趟操作的运行时间为 Θ(E)。第 6-7 行的 for 循环运行时间为 O(E)。
4. 核心代码：

for (var i = 0; i < n - 1; i++) {
    for (var j = 0; j < m; j++) {//对m条边进行循环
      var edge = edges[j];
      // 松弛操作
      if (distance[edge.to] > distance[edge.from] + edge.weight ){ 
        distance[edge.to] = distance[edge.from] + edge.weight;
      }
    }
}

其中， n为顶点的个数，m为边的个数，edges数组储存了所有边，distance数组是源点到所有点的距离估计值，循环结束后就是最小值。
5. 例题
例如，下面的有向图 G 中包含 5 个顶点和 8 条边。假设源点 为 A。初始化 distSet 所有距离为 INFI，源点 A 为 0。