深度学习：GoogLeNet核心思想详细讲解

想法来源
- 时代局限性
- 稀疏运算特性
- - 稀疏矩阵
  - 稀疏运算
- 并行计算
- 结合稀疏与并行
Inception block
GoogLeNet
- Average pooling
- 辅助分类器
训练方法(Training Method)
- 超参数设置
- 模型集成
- - 训练阶段
  - 预测阶段
基于GoogLeNet的服装分类（Pytorch）
- 服装分类数据集
- 定义模型
- 测试数据
- 训练模型

💡 在2014年的ImageNet图像识别挑战赛中，一个名叫GoogLeNet [Szegedy et al., 2015]的网络架构大放异彩。
GoogLeNet吸收了NiN中串联网络的思想，并在此基础上做了改进。这篇论文的一个重点是解决了什么样大小的卷积核最合适的问题。
毕竟，以前流行的网络使用小到1 * 1，大到5 * 5的卷积核。本文的一个观点是，有时使用不同大小的卷积核组合是有利的。
在本节中，我们将介绍一个稍微简化的GoogLeNet版本：我们省略了一些为稳定训练而添加的特殊特性，现在有了更好的训练方法，这些特性不是必要的。

想法来源

时代局限性

如果想提高模型的性能，作者认为：当模型的层数足够深，标注好的数据足够多的时候，那么将很高效的训练出一个精度不错的模型。但是这个方案有两个缺点：

数据越多就意味着参数越多，但是就很容易面临着overfitting，当我们标注高质量的时，成本很昂贵，比如我们要标注下面的数据：

这两张图片在我们看来都是二哈，但是它们是两个不同的品种，普通人往往无法标注这些精细的数据，就需要专家标注。
在深度神经网络中，我们增加一个卷积层，参数量平方倍增长，但是那个年代算力是有限的，跑起来也就十分昂贵。增加的卷积层，会造成很多的权重为0，因为ReLU激活函数与卷积神经网络的局部连接（当采用gpu并行计算时），会造成计算资源的浪费。

稀疏运算特性

稀疏矩阵

在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵；与之相反，若非0元素数目占大多数时，则称该矩阵为稠密矩阵。定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。

稀疏运算

在这里插入图片描述

根据上面的缺点，作者认为我们应该把全连接层替换成稀疏连接结构，这样就可以避免计算资源的浪费，加速收敛。
作者还提到了Hebbian principle，主旨是：

如果突触两侧的两个神经元（即连接）同时被激活，则该突触的强度会选择性地增加。
如果突触两侧的两个神经元被异步激活，则该突触被选择性地削弱或消除。

并行计算

随着现在计算硬件的飞速发展，我们如果在gpu上用稀疏计算，那么它的效率将为减少100倍，无论我们怎么调试，它的效果都不尽人意，所以作者认为要充分利用gpu并行计算。

结合稀疏与并行

作者想要找到一个鱼与熊掌兼得的方案，在使用稀疏运算的优势的同时，还要充分利用GPU。
利用稀疏矩阵分解成密集矩阵计算的原理来加快收敛速度。举个例子下图左侧是个稀疏矩阵（很多元素都为0，不均匀分布在矩阵中），和一个2x2的矩阵进行卷积，需要对稀疏矩阵中的每一个元素进行计算；如果像右图那样把稀疏矩阵分解成2个子密集矩阵，再和2x2矩阵进行卷积，稀疏矩阵中0较多的区域就可以不用计算，计算量就大大降低。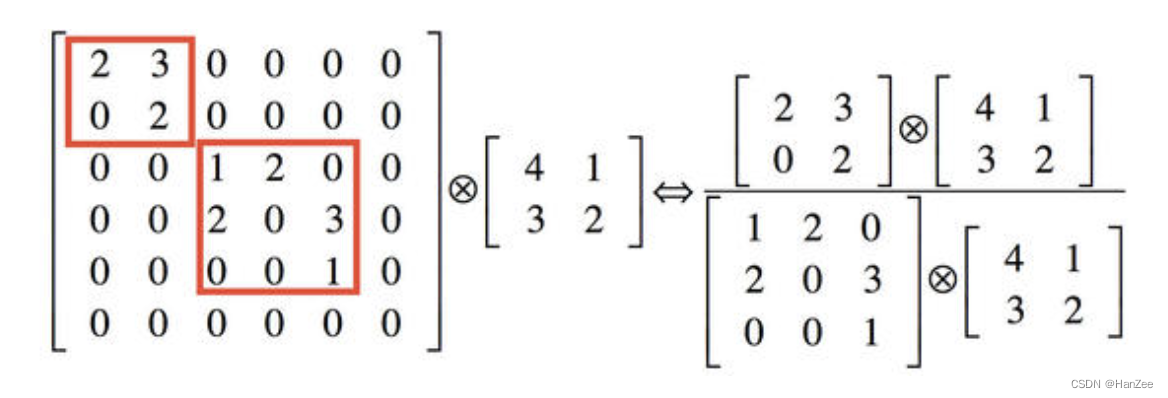在这里插入图片描述
但是这些都是作者的假设，他也不能合理的解释其原因。

Inception block

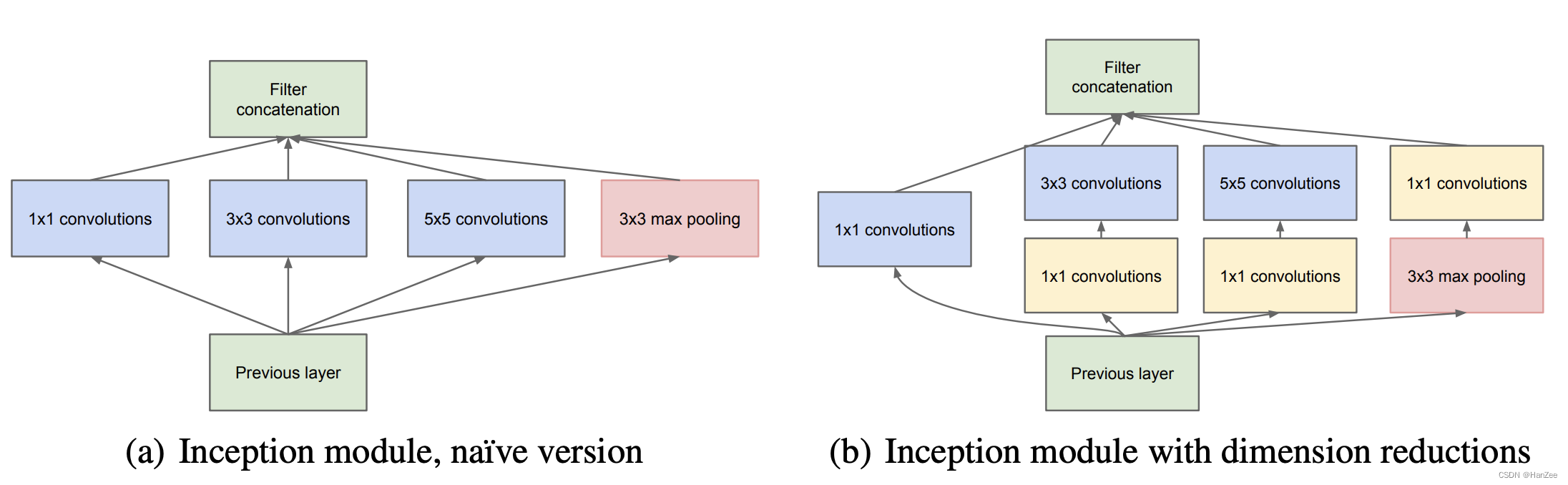
在这里插入图片描述
Inception的主要思想是找到一个拥有稀疏连接的卷积神经网络局部计算并且近似的并行计算的计算方式。是传统的vgg、alexnet的串联结构不用，第一个版本左图 a，采用了并行的结构，分别采用 1 * 1，3 * 3， 5 * 5，的卷积和池化对previous层同时提取特征，然后把这些卷积核的输出尺寸固定，最后把他们堆叠到一起，这就是Inception块。
它的优点是可以提取到不同尺度的信息，意味着特征更多，分类更准确，缓解了串行卷积层特征丢失的问题（由于感受野限制）。
但是左图由于大量的使用5 * 5卷积，计算量也随之水涨船高，作者根据Network in Network这篇论文，具体细节参考之前的文章。通过1 * 1 卷积，先降维，在升维，减少了参数量，增加了模型的表达能力（非线性）。于是就有右图b。

GoogLeNet

请添加图片描述

Average pooling

网络一共22层，为了减少参数作者把alexnet的两层全连接层换成了全局平均池化，数据有多少类别，最后的channel数就是多少，把每个channel的feature换成这个channel所有feature的平均值，再经过soft Max。最终通过实验发现，利用average pooling的精度比全连接层好了6%。

辅助分类器

它的作用主要是在浅层设置分类器来缓解梯度消失，其中作者在之后的论文中提到这种方法效果不理想，就把这个结构删除了，本文就不在过多描述。

训练方法(Training Method)

超参数设置

dropout：0.7
SGDM：momentum=0.9
learning rate：decreasing learning rate by 4% every 8 epoch。

模型集成

训练阶段

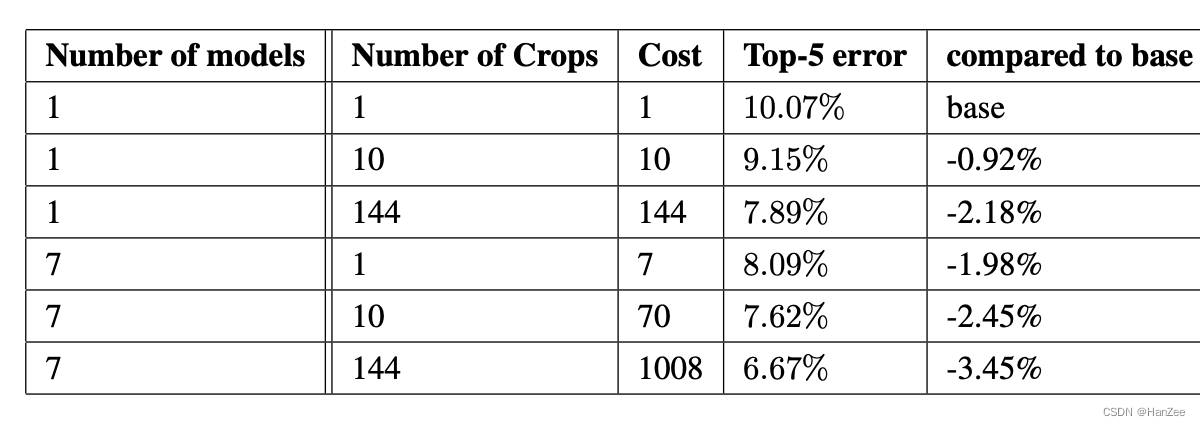
作者训练了7个模型，这七个模型有相同的学习率策略，模型结构，初始化权重（由于作者的疏忽）。
不同点：根据不同的图像采样，随机的图像输入顺序。

预测阶段

把图像根据短边resize四个尺寸，分别为256、288，320、352。
每个尺寸在根据左中右，上中下分别裁剪出三个小图。
把每张小图取四个角和中央，然后resize 224 * 224。
然后每张图做一个镜像操作。
根据上述操作，每张图可以变成4 * 3 * 6 * 2 = 144张，然后对结果取均值。

基于GoogLeNet的服装分类（Pytorch）

服装分类数据集

我们可以通过框架中的内置函数将Fashion-MNIST数据集下载并读取到内存中。

# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，
# 并除以255使得所有像素的数值均在0到1之间
def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)#通过compose组合多个操作
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=4),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=4))
                            #num workers 为线程数

定义模型


import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1,1)),
                   nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

测试数据

def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
    """使用GPU计算模型在数据集上的精度"""
    if isinstance(net, nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)#累加器
    
    with torch.no_grad():#禁止计算梯度
        for X, y in data_iter:
            if isinstance(X, list):
                # BERT微调所需的（之后将介绍）
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

训练模型

#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()#更新参数
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
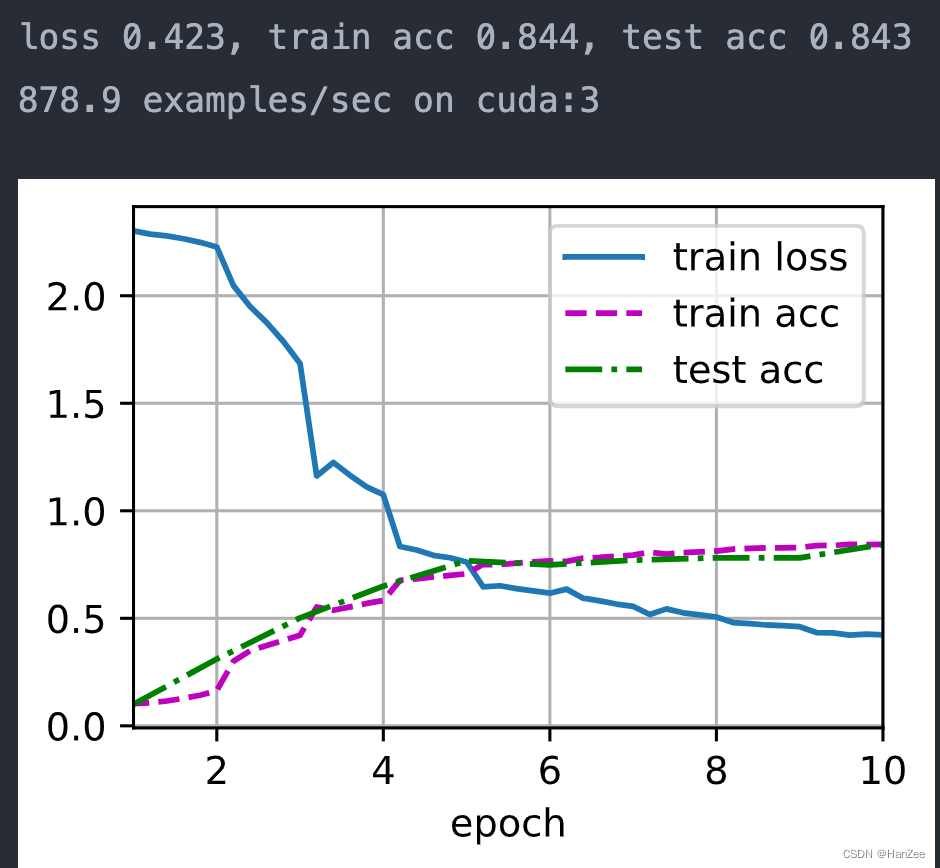
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

train_iter, test_iter = load_data_fashion_mnist(256, resize=224)
train_ch6(net, train_iter, test_iter, 10, 0.01, d2l.try_gpu())