有营养的算法笔记(八）

news2024/11/16 5:41:40

有营养的算法笔记八

    • 摆砖块问题
    • 数字转换
    • K递增子序列
    • 魔法子数组

摆砖块问题

1.题目描述

给定一个正数数组arr，其中每个值代表砖块长度。所有砖块等高等宽，只有长度有区别，每一层可以用1块或者2块砖来摆。要求每一层的长度一样
要求必须使用所有的砖块，请问最多摆几层

2.解题思路

首先我们可以将数组arr排个序。然后了本题使用双指针的方法就能够搞定，就只有两种可能性。首先我们就要想了砖块长度最大的砖块，它就只有两种选择第一种选择自己单独作为一层，第二种选择就只能和砖块长度最小的砖块作为一层，可能就有老铁问了为什么只能和长度最小的砖块作为一层，这是因为题目要求砖块必须都用，并且每一层的宽度要一样。此时如果宽度最长的和其它的砖块结合了，那么长度最小的和谁配了？所以长度最长的只能和长度最短的配。就只有这两种可能性将这两种可能性的答案累加起来就是答案。

3.对应代码

#include<iostream>
using namespace std;
//给定一个正数数组arr，其中每个值代表砖块长度
//所有砖块等高等宽，只有长度有区别
//每一层可以用1块或者2块砖来摆
//要求每一层的长度一样
//要求必须使用所有的砖块
//请问最多摆几层

/*
*  可能性1：长度最长的单独为一层
*  可能性2：长度最长的搭配一个一起使用，此时一定是最大值搭配最小值一起使用，因为所有要一起用
* 
*/
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
class Soulution
{
public:
	int maxLevel(vector<int>& nums)
	{
		int N = nums.size();
		if (N < 2) {
			return 1;
		}
		sort(nums.begin(), nums.end());
		//可能性1:最大长度的砖块单独作为一层
		//可能性2：搭配一个但是一定是和最小的那个一起使用
		int p1 = level(nums, nums[N - 1]);
		int p2 = level(nums, nums[N - 1] + nums[0]);
		return max(p1, p2);

	}
	int level(vector<int>& nums, int len) {
		int ans = 0;
		int L = 0;
		int R = nums.size() - 1;
		while (L <= R)
		{
			//单独使用
			if (nums[R] == len) {
				R--;
				ans++;
			}
			//两个一起用不能是同一个位置
			else if (L <R && nums[L] + nums[R] == len) {
				L++;
				R--;
				ans++;
			}
			else {
				return -1;
			}
		}
		return ans;
	}
};
int main()
{
	vector<int>arr{90, 10, 20,80,50};
	cout << Soulution().maxLevel(arr) << endl;
	return 0;
}

数字转换

1.题目描述

给定一个字符串形式的数，比如"3421"或者"-8731"，如果这个数不在 - 32768~32767范围上，那么返回"NODATA"。如果这个数在 - 32768~32767范围上，那么这个数就没有超过16个二进制位所能表达的范围，返回这个数的2进制形式的字符串和16进制形式的字符串，用逗号分割。

2.解题思路

本题的解题思路很简单直接干就是了。首先我们可以将这个字符串转换问为一个int类型的整数。在这之前我们可以判断一下这个字符串的长度是否超过6位如果超过了直接返回“NODATA"即可。因为-32768~32767长度最长也就只有6位，所以如果超过了6位我们返回即可。将其转换为整型之后，我们把低16位的数据提取出来即可。如何提取了我们只需要使用0xffff和转换的这个数字按位与即可。这样一来16个比特位的信息我们都有了，二进制形式直接遍历即可是1就填1是0就填0.现在我们只要把16进制搞定了这道题就做完了
而十六进制我们只需要每次提取4位根据他的值进行判断即可。具体我们看看代码吧

3.对应代码

#include<iostream>
#include<string>
using namespace std;
class Solution
{
public:
	string convert(string num)
	{
		if (num.empty() || num.size() > 6) {
			return "NODATA";
		}
		int n= stoi(num);
		//将15位全部给取出来
		int info = (n < 0 ? (1 << 15) : 0) | (n & 0xffff);
			//注意65535代表的是16个全1
			string ans;
			for (int i = 15; i >= 0; i--) {
				ans += (info & (1 << i)) ? '1' : '0';
			}
			ans += ",";
			ans += "0x";
			for (int i = 12; i >= 0; i -= 4) {
				int cur = ((0xf << i) & info) >> i;
				//从高位开始取每次取四位获得其值然后在进行判断
				if (cur < 10) {
					ans += (cur + '0');
				}
				else
				{
					ans += (cur - 10 + 'a');
				}


			}
			return ans;

	}
};
int main()
{
	cout << Solution().convert("-1") << endl;
	cout << Solution().convert("457") << endl;
	cout << Solution().convert("32767") << endl;

	return 0;
}

K递增子序列

1.对应letecode链接

k递增子序列

2.题目描述
在这里插入图片描述
3.解题思路

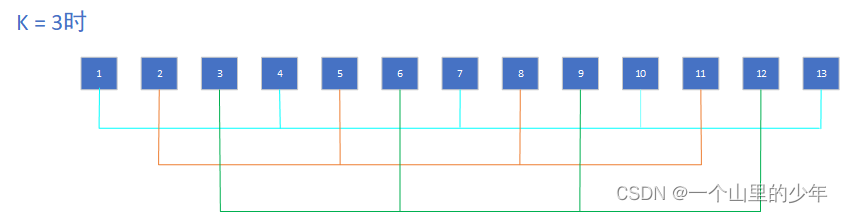
本题其实是最长递增子序列的变形题。这题也有点这个希尔排序分支的意思。按照题目的意思我们可以将没k 个数取一个元素，分为若干组，例如当 k=3时
arr[0],arr[3],arr[6],⋯
arr[1],arr[4],arr[7],⋯
arr[2],arr[5],arr[8],⋯
下面我们看一张图就更清楚了
在这里插入图片描述
将这个数组分成k组之后，我们分别求每一组里面最长不严格递增子序列的长度，在用这一组的个数减去最长不严格递增子序列的长度就是需要修改的次数。在这里需要注意的是每一组的元素个数可能不相同，假设数组的长度为N，那么最多只有（N+k-1）/k也就是N/K向上取整个元素。每一组我们都这么干，将每一组需要修改的次数累加上来最终就是我们想要的答案。

4.对应代码

class Solution {
  public:
    int kIncreasing(vector<int>& arr, int k) {

        int N = arr.size();
        int len = (N + k - 1) / k; //向上取整
        vector<int>heple(len);

        int ans = 0;
        for (int i = 0; i < k; i++) {
            ans += Need(arr, heple, i, k);
        }
        return ans;
    }

    //计算每每一组需要修改多少个
    int Need(vector<int>& nums, vector<int>& heple, int start, int k) {
        int size = 0;
        int num = 0;
        //记录这一组有多少个数
        for (int i = start; i < nums.size(); i += k, num++) {
            //每次更新最长不严格递增子序列的长度
            size = Insert(heple, nums[i], size);

        }
        return num - size;
    }

    int Insert(vector<int>& heple, int target, int size) {
        int L = 0;
        int R = size - 1;
        int ans = size;
        //进行二分查找到大于target最左边的位置
        while (L <= R) {
            int mid = L + (R - L) / 2;

            if (heple[mid] > target) {
                ans = mid;
                R = mid - 1;
            } else {
                L = mid + 1;
            }

        }
        heple[ans] = target;
        return ans == size ? size + 1 : size;
        //返回最长不严格递增子序列的长度
    }

};

思考？如果从非递减改成严格递增此时又该怎么做?

把每个数减去其下标，然后对所有正整数求最长非降子序列。

举个例子，现在每 k 个数选一个数，假设选出来的数组是 [3,2,4,5,5,6,6]。

每个数减去其下标后就是 [3,1,2,2,1,1,0]。

对这个数组中的正整数求最长非降子序列，那就是 [1,1,1]了，对应原始数组的 [,2,,,5,6,]，这三个数字保留，其余数字修改完成后就是 [1,2,3,4,5,6,7]，符合严格递增且均为正整数的要求。

注：上述减去下标的技巧，主要是为了能让保留的数字之间可以容纳严格递增的数字。否则，若直接按照最长严格递增子序列的求法，会得到例如 [,2,4,5,,6,*] 这样的错误结果。

思路来自于这位大佬

思路来源

魔法子数组

1.题目描述

来自美团
小美有一个长度为n的数组，为了使得这个数组的和尽量大，她向会魔法的小团进行求助。小团可以选择数组中至多两个不相交的子数组，并将区间里的数全都变为原来的10倍，小团想知道他的魔法最多可以帮助小美将数组的和变大到多少?

2.解题思路

本题难度很大个人认为？首先我们说一下暴力方法。首先我们求一个数组的累加和数组，从[0…N-1)范围内枚举划分点。假设划分点为split,那么对应这个划分点我们可以求[0…split]范围内最多有一个魔法子数组的情况下最大累加和是多少，[split…N-1]范围内最多有一个魔法子数组的情况下最大累加和是多少。把这两个区间的累加和加起来就是当前划分点所能获得的最大累加和，然后我们在尝试下一个划分点，更新答案。每个划分点我们都这样搞那么答案一定就在其中。那么如何求一个范围内最多有一个魔法子数组的最大累加和了？
第一种情况就是这个范围不使用魔法，那么就是原始数组的累加。
第二种情况需要使用魔法，此时我们可以枚举这个范围内所有的子数组对这个子数组使用魔法其它子数组加上原始累加和即可。

3.对应代码

int maxSum1(vector<int>& nums)
	{
		int N = nums.size();
		vector<int>sum(N);
		sum[0] = nums[0];
		//生成累加和数组
		for (int i = 1; i < N; i++) {
			sum[i] = sum[i - 1] + nums[i];
		}
		int ans = INT_MIN;
		for (int split = 0; split < N - 1; split++) {
			/*枚举划分点求[0...split]范围内最多有一个魔法子数组的情况下最大累加和是多少
			* [split....N-1]范围内最多有一个魔法子数组的情况下最大累加和是多少
			* 我们把所有情况全部枚举一遍答案一定就在其中
			*/
			
			int curSum = MostMaxSum(sum, 0, split) + MostMaxSum(sum, split + 1, N - 1);
			
			ans = max(ans, curSum);
            
		}

		return ans;

	}
	

	

private:
	//求区间[L.....R]范围内的累加和
	int GetSum(vector<int>& sum, int L, int R) {

		return L > R ? 0 : (L == 0 ? sum[R] : sum[R] - sum[L - 1]);
	}

	int MostMaxSum(vector<int>& sum, int L, int R) {
		if (L > R)return 0;//区间不存在

		int ans = GetSum(sum, L, R);
		//首先设置为没有魔法子数组的情况
		for (int start = L; start <= R; start++) {
			//枚举[L.....R]范围内所有的子数组
			for (int end = L; end <= R; end++) {

				int curSum = GetSum(sum, start, end) * 10 + GetSum(sum, L, start - 1) + GetSum(sum, end + 1, R);
				//选择[start,end]这个子数组进行操作魔法操作其它区间我们只需要获取累加和就是了
				ans = max(curSum, ans);
			}
		}
		return ans;
	}

但是获取每个范围内最大累加和我们是使用暴力枚举的方式进行的。如果我们能够省掉这个枚举那么这个时间复杂度就变为了线性时间。下面我们来介绍一下dp的方法是如何来实现的。下面我们解释一下dp[i]的含义
dp[i]的含义代表arr[0…i]最多有一个魔法子数组的最大累加和，如果我们能够求出来，那么我们在反着求一遍.即dp1[i]代表这个arr[i…N-1]范围内最多有一个魔法子数组的情况下最大累加和是多少。如果我们能够求出来那么我们只需要将其拼接起来就可以了。下面我们我们来分析一下可能性

  • 可能性1：arr[0…i]不使用魔法也就是没有这个魔法子数组，那么最大累加和就是原始数组[0…i]范围内的累加和。
  • 可能性2：arr[0…i]范围内存在魔法子数组那么此时就又有两种小情况了。

下面我们一个一个来分析这两种小情况的可能性
可能性1：arr[i]不在10倍区域里面，那么此时答案就是arr[i]+dp[i-1]也就是当前位置的值+arr[0…i-1]范围内最多只有一个魔法数组的最大累加和
可能性2：arr[i]在10倍区域里面，此时我们有要分情况了
1.arr[i]单独在10倍区域里面，此时结果为arr[i]*10+arr[0…i-1]范围内的累加和
2.arr[i]决定往左边扩但是此时干了我们不知道他要扩多远。

对于这种情况我们该如何解决了此时我们需要知道arr[0…i-1]范围内i-1位置必须在10倍区域里面的情况下最大累加和是多少。因此我们需要在定义一个动态规划magic[i]，他的含义是arr[i]必须在10倍区域里面最大累加和是多少。这个动态规划求起来很简单。第一种情况就是arr[i]位置单独，第二种情况就是往左扩那么不就是arr[i]*10+magic[i-1]吗？然后我们在反着求一遍。这个问题就解决了

#include<iostream>
#include<vector>
using namespace std;

//* 
//来自美团
//小美有一个长度为n的数组，
//为了使得这个数组的和尽量大，她向会魔法的小团进行求助
//小团可以选择数组中至多两个不相交的子数组，
//并将区间里的数全都变为原来的10倍
//小团想知道他的魔法最多可以帮助小美将数组的和变大到多少?


//这题巨难


class Solution
{
public:
	int maxSum1(vector<int>& nums)
	{
		int N = nums.size();
		vector<int>sum(N);
		sum[0] = nums[0];
		//生成累加和数组
		for (int i = 1; i < N; i++) {
			sum[i] = sum[i - 1] + nums[i];
		}
		int ans = INT_MIN;
		for (int split = 0; split < N - 1; split++) {
			/*枚举划分点求[0...split]范围内最多有一个魔法子数组的情况下最大累加和是多少
			* [split....N-1]范围内最多有一个魔法子数组的情况下最大累加和是多少
			* 我们把所有情况全部枚举一遍答案一定就在其中
			*/
			
			int curSum = MostMaxSum(sum, 0, split) + MostMaxSum(sum, split + 1, N - 1);
			
			ans = max(ans, curSum);
            
		}

		return ans;

	}
	
	int maxSum2(vector<int>& nums)
	{
		int N = nums.size();
		if (N == 0) {
			return 0;
		}

		if (N == 1) {
			return max(nums[0], nums[0] * 10);
		}

		//
		int sum = nums[N - 1];
		vector<int>right(N);
		right[N - 1] = max(nums[N - 1], nums[N - 1] * 10);

		int magic = nums[N - 1] * 10;
		//这个就是magic数组这里我们使用了空间压缩
		for (int i = N - 2; i >= 0; i--) {

			magic = nums[i] * 10 + max(sum, magic);
			//magic的转移方程
			//等价于max(nums[i]*10+sum,magic+nums[i]*10);
			sum += nums[i];
			//累加和
			right[i] = max(right[i + 1] + nums[i], max(sum, magic));


		}

		int ans = INT_MIN;
		sum = nums[0];
		int dp = max(sum, sum * 10);
		magic = nums[0] * 10;
		ans = max(ans, dp + right[1]);
		for (int i = 1; i < N - 1; i++) {
			magic = nums[i] * 10 + max(sum, magic);
			sum += nums[i];
			dp = max(dp + nums[i], max(magic, sum));
			//每个位置求出答案更新
			ans = max(ans, dp + right[i + 1]);
		}
		return ans;

	}
	

private:
	//求区间[L.....R]范围内的累加和
	int GetSum(vector<int>& sum, int L, int R) {

		return L > R ? 0 : (L == 0 ? sum[R] : sum[R] - sum[L - 1]);
	}

	int MostMaxSum(vector<int>& sum, int L, int R) {
		if (L > R)return 0;//区间不存在

		int ans = GetSum(sum, L, R);
		//首先设置为没有魔法子数组的情况
		for (int start = L; start <= R; start++) {
			//枚举[L.....R]范围内所有的子数组
			for (int end = L; end <= R; end++) {

				int curSum = GetSum(sum, start, end) * 10 + GetSum(sum, L, start - 1) + GetSum(sum, end + 1, R);
				//选择[start,end]这个子数组进行操作魔法操作其它区间我们只需要获取累加和就是了
				ans = max(curSum, ans);
			}
		}
		return ans;
	}
	
};
vector<int>GetRandom(int len, int v)
{
	vector<int>nums;
	for (int i = 0; i < len; i++)
	{
		int val = rand() % v - rand() % v;
		nums.push_back(val);
	}
	return nums;
}
int main()
{
	/*vector<int>arr{ 3, -4, 5, 1, -3 };
	cout << Solution().maxSum2(arr) << endl;*/
	int times = 1020;
	int len = 10;
	int v = 100;
	for (int i = 0; i < times; i++) {
		
		vector<int>nums = GetRandom(len, v);
		int ans1 = Solution().maxSum1(nums);
		int ans2 = Solution().maxSum2(nums);
		if (ans1 != ans2) {
			cout << "错了" << endl;
			return 1;
		}
	}
	cout << "测试完毕对了" << endl;
	return 0;
}

对应测试代码

#include<iostream>
#include<vector>
using namespace std;

//* 
//来自美团
//小美有一个长度为n的数组，
//为了使得这个数组的和尽量大，她向会魔法的小团进行求助
//小团可以选择数组中至多两个不相交的子数组，
//并将区间里的数全都变为原来的10倍
//小团想知道他的魔法最多可以帮助小美将数组的和变大到多少?


//这题巨难


class Solution
{
public:
	int maxSum1(vector<int>& nums)
	{
		int N = nums.size();
		vector<int>sum(N);
		sum[0] = nums[0];
		//生成累加和数组
		for (int i = 1; i < N; i++) {
			sum[i] = sum[i - 1] + nums[i];
		}
		int ans = INT_MIN;
		for (int split = 0; split < N - 1; split++) {
			/*枚举划分点求[0...split]范围内最多有一个魔法子数组的情况下最大累加和是多少
			* [split....N-1]范围内最多有一个魔法子数组的情况下最大累加和是多少
			* 我们把所有情况全部枚举一遍答案一定就在其中
			*/
			
			int curSum = MostMaxSum(sum, 0, split) + MostMaxSum(sum, split + 1, N - 1);
			
			ans = max(ans, curSum);
            
		}

		return ans;

	}
	

	

private:
	//求区间[L.....R]范围内的累加和
	int GetSum(vector<int>& sum, int L, int R) {

		return L > R ? 0 : (L == 0 ? sum[R] : sum[R] - sum[L - 1]);
	}

	int MostMaxSum(vector<int>& sum, int L, int R) {
		if (L > R)return 0;//区间不存在

		int ans = GetSum(sum, L, R);
		//首先设置为没有魔法子数组的情况
		for (int start = L; start <= R; start++) {
			//枚举[L.....R]范围内所有的子数组
			for (int end = L; end <= R; end++) {

				int curSum = GetSum(sum, start, end) * 10 + GetSum(sum, L, start - 1) + GetSum(sum, end + 1, R);
				//选择[start,end]这个子数组进行操作魔法操作其它区间我们只需要获取累加和就是了
				ans = max(curSum, ans);
			}
		}
		return ans;
	}
	int maxSum2(vector<int>& nums)
	{
		int N = nums.size();
		if (N == 0) {
			return 0;
		}

		if (N == 1) {
			return max(nums[0], nums[0] * 10);
		}

		//
		int sum = nums[N - 1];
		vector<int>right(N);
		right[N - 1] = max(nums[N - 1], nums[N - 1] * 10);
		
		int magic = nums[N - 1] * 10;
		//这个就是magic数组这里我们使用了空间压缩
		for (int i = N - 2; i >= 0; i--) {

			magic = nums[i] * 10 + max(sum, magic);
			//magic的转移方程
			//等价于max(nums[i]*10+sum,magic+nums[i]*10);
			sum += nums[i];
			//累加和
			right[i] = max(right[i + 1] + nums[i], max(sum, magic));


		}

		int ans = INT_MIN;
		sum = nums[0];
		int dp = max(sum, sum * 10);
		magic = nums[0] * 10;
		ans = max(ans, dp + right[1]);
		for (int i = 1; i < N - 1; i++) {
			magic = nums[i] * 10 + max(sum, magic);
			sum += nums[i];
			dp = max(dp + nums[i], max(magic, sum));
			//每个位置求出答案更新
			ans = max(ans, dp + right[i + 1]);
		}
		return ans;

	}
};
vector<int>GetRandom(int len, int v)
{
	vector<int>nums;
	for (int i = 0; i < len; i++)
	{
		int val = rand() % v - rand() % v;
		nums.push_back(val);
	}
	return nums;
}
int main()
{
	/*vector<int>arr{ 3, -4, 5, 1, -3 };
	cout << Solution().maxSum2(arr) << endl;*/
	int times = 1020;
	int len = 10;
	int v = 100;
	for (int i = 0; i < times; i++) {
		
		vector<int>nums = GetRandom(len, v);
		int ans1 = Solution().maxSum1(nums);
		int ans2 = Solution().maxSum2(nums);
		if (ans1 != ans2) {
			cout << "错了" << endl;
			return 1;
		}
	}
	cout << "测试完毕对了" << endl;
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1616.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【阅读笔记】低照度图像增强-《An Integrated Neighborhood Dependent...

【阅读笔记】低照度图像增强-《An Integrated Neighborhood Dependent...

本文介绍的是一种比较实用的低照度图像增强算法&#xff0c;选自2004年Tao的一篇论文&#xff0c;名称是《An Integrated Neighborhood Dependent Approach for Nonlinear Enhancement of Color Images 》 概述 图像中暗区图像增强的基本机制是对图像的亮度进行动态范围压缩&…
阅读更多...
玩转rancher 2.6之 monitor监控

玩转rancher 2.6之 monitor监控

目录 前言 1. 安装monitor 2. 安装prometheus-webhook-dingtalk 2.1 配置钉钉告警配置文件 2.2 创建钉钉告警模板 2.3 创建dingtalk configmap配置文件 2.4 安装dingtalk 2.5 dingtalk调用方法 3. 配置告警 3.1 配置告警接收者 3.2 配置路由默认告警接收者 4. 测试 前…
阅读更多...
初识C++ （三）

初识C++ （三）

初识C 三引用一. 引用的概念代码演示二. 引用特性1. 引用在定义时必须要初始化2. 一个引用可以有多个实体3. 引用一旦引用一个实体&#xff0c;再不能引用其他实体三. 使用场景1. 做参数2. 做返回值内存销毁后空间还在吗&#xff1f;内存销毁后我们还能访问嘛&#xff1f;结论优…
阅读更多...
论文写作——ICASSP论文写作及投稿

论文写作——ICASSP论文写作及投稿

记录 ICASSP2023 写作投稿过程。小白如何写好并投稿自己的第一篇英文论文&#xff1f;投稿会议时&#xff08;以 ICASSP2023 为例&#xff09;有哪些需要关注的信息以及注意事项&#xff1f;论文写作必备软件有哪些&#xff1f;论文书写关注点有哪些&#xff1f;论文格式与排版…
阅读更多...
【Node.JS 】http的概念及作用

【Node.JS 】http的概念及作用

往期文章 【Node.JS 练习】时钟案例 【Node.JS 】path路径模块 【Node.JS 练习】考试成绩整理 【Node.JS】buffer类缓冲区 【Node.JS】事件的绑定与触发 【Node.JS】写入文件内容 【Node.JS】读取文件内容 什么是http模块 在网络节点中&#xff0c;负责消费资源的电脑&…
阅读更多...
【C语言】C语言文件操作详解（一）

【C语言】C语言文件操作详解（一）

前言 本章主要讨论的是数据文件&#xff0c;如何使用C语言对数据文件进行输入输出数据的操作&#xff0c;以及文件顺序读写涉及的库函数详解 目录前言1.为什么使用文件2.什么是文件2.1程序文件2.2数据文件2.3文件名3.文件的打开和关闭3.1文件指针3.2文件的打开3.3文件的关闭3.…
阅读更多...
初识JAVA

初识JAVA

文章目录初识 java 的 main 方法main 方法示例运行Java程序注释基本规则注释规范标识符关键字初识 java 的 main 方法 main 方法示例 public class test {public static void main(String[] args) {System.out.println("hello world!");} }如果我们学的C语言&#…
阅读更多...
DASCTF X GFCTF 2022十月挑战赛 Writeup

DASCTF X GFCTF 2022十月挑战赛 Writeup

文章目录WEBEasyPOPMISC滴滴图ez_xxdpoi&#xff1f;qoi&#xff01;easy_dotsdockermiscWEB EasyPOP Fast Destruct优先一步__wakeup()执行析构函数 从一道题看fast_destruct fine::__invoke() <- sorry::__get() <- secret_code::show() <- secret_code::__call…
阅读更多...
使用 MySQL 日志 - Part 1

使用 MySQL 日志 - Part 1

在软件应用程序中&#xff0c;日志文件会记录系统中执行的操作以及执行操作的人员。如果出现意外情况&#xff0c;无论是安全漏洞、系统崩溃还是性能迟缓&#xff0c;日志文件都可以成为管理员的得力助手。MySQL 就有几个不同的日志文件&#xff0c;可以帮助你找出 MySQL 服务器…
阅读更多...
Excel多条件计数——COUNTIFS【获奖情况统计】

Excel多条件计数——COUNTIFS【获奖情况统计】

问题描述 当前&#xff0c;我们需要对表格中的获奖情况进行统计 奖励级别&#xff1a;院级、校级、国家级、国际级奖励内容&#xff1a;特等奖、一等奖、二等奖、三等奖、优胜奖 功能要求 对所有奖励级别进行统计根据级别&#xff0c;计算内容数量 当有人的选项内容如下时 …
阅读更多...
MySQL之SQL的执行流程

MySQL之SQL的执行流程

MySQL之SQL的执行流程MySQL架构连接层服务层存储引擎连接查看连接连接与线程连接超时最大连接会话与全局查询缓存语法解析和预处理词法解析语法解析预处理查询优化器优化器查询执行计划存储引擎存储引擎概述常用存储引擎MyISAMInnoDBMEMORY存储引擎的选择执行引擎MySQL架构 从…
阅读更多...
DBMS 中的 2 层架构与 3 层架构

DBMS 中的 2 层架构与 3 层架构

有多种方法可以获取存储在数据库管理系统中的数据。根据其结构对 DBMS 的体系结构进行了分类。 DBMS 架构概述 理解 2-tier 和 3-tier 架构是一个相当重要的话题&#xff0c;不仅对于学术或寻找好工作&#xff0c;而且对于与技术相关的一般意识也是如此。 2-tier simple表示两…
阅读更多...
【每日渗透笔记】覆盖漏洞+修改隐藏数据实战尝试

【每日渗透笔记】覆盖漏洞+修改隐藏数据实战尝试

目录 一、特点&#xff1a; 1.1、特征&#xff1a; 1.2、知识&#xff1a; 1.3、注册的功能点&#xff1a; 目前&#xff1a; 问题&#xff1a; 二、分析数据包 2.1、修改数据处 三、换思路 一、特点&#xff1a; 1.1、特征&#xff1a; 存在注册的功能点 1.2、知识&a…
阅读更多...
资本狂欢过后 Aptos如何顶住旧日光环？

资本狂欢过后 Aptos如何顶住旧日光环？

10月27日&#xff0c;Aptos Autumn主网上线一周后&#xff0c;其浏览器数据显示&#xff0c;该Layer1网络的交易总量为1432万笔&#xff0c;TPS为10.65&#xff0c;原生Token APT总供应量约为10.02亿&#xff0c;质押数量约为8.23亿枚&#xff0c;活跃节点数量102个。 低TPS、高…
阅读更多...
AIR780E使用AT连接TCP收发数据

AIR780E使用AT连接TCP收发数据

最近各种技术群都被合宙9.9的开发板刷屏了&#xff0c;笔者成功的第一时间拼团成功&#xff0c;已经作为前两百人收到开发板了&#xff0c;因为官方的二次开发固件还没出&#xff0c;就先玩一下传统的AT开发。 文中各种文档和资料均可以在air780e.cn网站找到。 本文将介绍如何…
阅读更多...
99208-90-9_炔基-棕榈酸_Alkynyl Palmitic Acid 可进行定制

99208-90-9_炔基-棕榈酸_Alkynyl Palmitic Acid 可进行定制

一、产品简介----Product introduction&#xff1a; 货号&#xff1a;Y-CL-0063 CAS&#xff1a;99208-90-9 中文名&#xff1a; 15-十六碳炔酸&#xff0c;炔基-棕榈酸 英文名&#xff1a;Alkynyl Palmitic Acid/hexadec-15-ynoic acid 结构式&#xff08;Structural&#xff…
阅读更多...
深度学习：GoogLeNet核心思想详细讲解（原创）

深度学习：GoogLeNet核心思想详细讲解（原创）

深度学习&#xff1a;GoogLeNet核心思想详细讲解想法来源时代局限性稀疏运算特性稀疏矩阵稀疏运算并行计算结合稀疏与并行Inception blockGoogLeNetAverage pooling辅助分类器训练方法(Training Method)超参数设置模型集成训练阶段预测阶段基于GoogLeNet的服装分类&#xff08;…
阅读更多...
WordPress 6.1新功能 (特性和截图)

WordPress 6.1新功能 (特性和截图)

WordPress 6.1 Beta 于几天前发布&#xff0c;预计将于 2022 年 11 月 1 日发布。这将是 2022 年的最后一个主要版本&#xff0c;将带来许多新功能和改进。 我们一直在密切监视开发并在我们的测试站点上尝试新功能。 在本文中&#xff0c;我们将通过功能和屏幕截图让您先睹为快…
阅读更多...
基于javaweb的医院管理系统(java+springboot+mybatis+vue+mysql)

基于javaweb的医院管理系统(java+springboot+mybatis+vue+mysql)

基于javaweb的医院管理系统(javaspringbootmybatisvuemysql) 运行环境 Java≥8、MySQL≥5.7、Node.js≥10 开发工具 后端&#xff1a;eclipse/idea/myeclipse/sts等均可配置运行 前端&#xff1a;WebStorm/VSCode/HBuilderX等均可 适用 课程设计&#xff0c;大作业&…
阅读更多...
对于一个即将上线的网站，如何测试

对于一个即将上线的网站，如何测试

web应用&#xff1a;也叫做网站&#xff0c;相对于客户端应用来说&#xff0c;web应用无需单独安装&#xff0c;在浏览器上即可使用其功能。 web应用的主要开发流程如下&#xff1a; 在网站开发的整个流程中&#xff0c;测试验收是上线发布前的最后一个环节&#xff0c;测试是…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023