文心一言 VS 讯飞星火 VS chatgpt （243）-- 算法导论18.1 1题

news2024/7/6 19:40:02

一、B树中为什么不允许最小度数 t=1？如果要写代码，请用go语言。

文心一言：

在B树中不允许最小度数 t=1 的主要原因在于这样会导致树的结构退化为链表，失去了B树作为平衡多路搜索树的优势。当 t=1 时，每个非根节点将只能包含最多一个关键字和两个子节点，这使得B树不再能够有效地利用空间，并且在搜索、插入和删除操作上性能会大大降低。

B树的设计初衷是为了减少树的高度，使得磁盘I/O操作次数最小化，特别是在数据库和文件系统中。当 t 值较小时，节点包含的关键字数量减少，树的高度增加，从而可能导致更多的磁盘I/O操作。因此，通常选择一个合适的 t 值来平衡树的深度和节点的关键字数量。

以下是一个简单的Go语言实现的B树节点的结构定义，用于展示B树节点的基本组成，但请注意这只是一个非常基础的框架，并不包含完整的B树操作实现。完整的B树实现会涉及更多的细节，如节点的分裂、合并、查找、插入和删除等操作。

package main  
  
import "fmt"  
  
// BTreeNode represents a node in a B-tree.  
type BTreeNode struct {  
    t       int       // Minimum degree (t) of the B-tree.  
    keys    []int     // Array of keys sorted in ascending order.  
    children []*BTreeNode // Array of child pointers.  
    isLeaf  bool      // Flag to indicate if this is a leaf node.  
}  
  
// NewBTreeNode creates a new B-tree node with the given minimum degree t.  
func NewBTreeNode(t int) *BTreeNode {  
    if t <= 1 {  
        panic("Minimum degree t must be greater than 1.")  
    }  
    return &BTreeNode{  
        t:      t,  
        keys:   make([]int, 0, 2*t-1),  
        children: make([]*BTreeNode, 0, 2*t),  
        isLeaf: true,  
    }  
}  
  
// InsertKey inserts a new key into the node.  
// This is a placeholder function and does not handle actual insertion logic.  
func (n *BTreeNode) InsertKey(key int) {  
    // In a real implementation, you would need to handle splitting the node  
    // if it becomes too full, as well as updating parent pointers and splitting  
    // child nodes if necessary.  
    fmt.Printf("Inserting key %d into node...\n", key)  
    // ... (implementation details omitted)  
}  
  
func main() {  
    // Create a B-tree node with minimum degree t=2.  
    node := NewBTreeNode(2)  
    fmt.Println("Created B-tree node:", node)  
  
    // Try to insert a key into the node.  
    // Note: This will not work as the actual insertion logic is not implemented.  
    // node.InsertKey(5)  
}

在上面的代码中，BTreeNode 结构体代表了一个B树的节点，它包含了节点的关键字数组 keys、子节点指针数组 children、一个布尔值 isLeaf 来标记是否是叶节点，以及最小度数 t。NewBTreeNode 函数用于创建一个新的B树节点，并在创建时检查 t 的值是否大于1。如果尝试使用 t=1 创建节点，将会触发一个 panic。

请注意，这只是一个非常基础的框架，并没有包含完整的B树操作。在实际应用中，你需要实现节点的分裂、合并、查找、插入和删除等操作，并确保它们符合B树的性质。由于这涉及很多细节和边界情况的处理，因此通常需要花费一定的时间和精力来正确实现这些功能。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

讯飞星火：

B树中不允许最小度数t=1，原因已经在上一个问题的回答中进行了解释。

下面是一个用Go语言实现的简单B树示例：

package main

import "fmt"

type BTreeNode struct {
    keys  []int
    child []*BTreeNode
}

func NewBTree(t int) *BTreeNode {
    return &BTreeNode{
        keys:  make([]int, 2*t-1),
        child: make([]*BTreeNode, 2*t),
    }
}

func (n *BTreeNode) IsLeaf() bool {
    return n.child[0] == nil
}

func (n *BTreeNode) Insert(key int) {
    i := len(n.keys) - 1
    if n.IsLeaf() {
        for i >= 0 && key < n.keys[i] {
            n.keys[i+1] = n.keys[i]
            i--
        }
        n.keys[i+1] = key
    } else {
        for i >= 0 && key < n.keys[i] {
            i--
        }
        i++
        if len(n.child[i].keys) == 2*t-1 {
            n.SplitChild(i, t)
            if key > n.keys[i] {
                i++
            }
        }
        n.child[i].Insert(key)
    }
}

func (n *BTreeNode) SplitChild(i int, t int) {
    z := NewBTree(t)
    y := n.child[i]
    n.child[i] = z
    z.child[0] = y.child[t]
    y.child[t] = nil
    for j := 0; j < t-1; j++ {
        z.keys[j] = y.keys[j+t]
    }
    y.keys = y.keys[:t-1]
    if !y.IsLeaf() {
        for j := 0; j < t; j++ {
            z.child[j+1] = y.child[j+t+1]
            y.child[j+t+1] = nil
        }
    }
    n.keys[i] = y.keys[t-1]
    y.keys = y.keys[:t-1]
}

func (n *BTreeNode) Print() {
    for i := 0; i < len(n.keys); i++ {
        fmt.Printf("%d ", n.keys[i])
    }
    fmt.Println()
    if !n.IsLeaf() {
        for _, c := range n.child {
            c.Print()
        }
    }
}

func main() {
    t := 3
    root := NewBTree(t)
    keys := []int{10, 20, 5, 6, 12, 30, 7, 17}
    for _, key := range keys {
        root.Insert(key)
    }
    root.Print()
}

这个示例中，我们定义了一个BTreeNode结构体，包含一个关键字数组和一个孩子节点数组。我们还实现了一些基本的B树操作，如插入和分裂子节点。最后，在main函数中，我们创建了一个新的B树，并插入了一些关键字，然后打印出整个树的结构。

360智脑：

在Go语言中，实现B树时通常会避免最小度数t=1的情况，以确保B树的性能优势。下面是一个简单的B树实现示例，其中最小度数t被设置为2，以展示如何插入和查找元素：

package main 
 
import (
	"fmt"
)
 
type BTreeNode struct {
	children []*BTreeNode 
	keys     []int 
	leaf     bool 
}
 
func NewBTreeNode(leaf bool) *BTreeNode {
	return &BTreeNode{
		children: make([]*BTreeNode, 2),
		keys:     make([]int, 2),
		leaf:     leaf,
	}
}
 
func (node *BTreeNode) Insert(key int) {
	if node.leaf {
		// 插入叶子节点 
		idx := len(node.keys)
		node.keys = append(node.keys, key)
		copy(node.keys[idx+1:], node.keys[idx:])
	} else {
		// 找到正确的子节点进行插入 
		idx := sort.SearchInts(node.keys, key)
		if idx < len(node.keys) && node.keys[idx] == key {
			// 已存在，无需插入 
			return 
		} else if idx < len(node.keys) {
			// 插入中间位置 
			node.keys[idx] = key 
		} else {
			// 插入到右侧子节点 
			node.children[idx].Insert(key)
		}
	}
}
 
func (node *BTreeNode) Search(key int) *BTreeNode {
	if node.leaf {
		// 叶子节点直接返回结果 
		for i, k := range node.keys {
			if key == k {
				return node 
			} else if key < k {
				return nil 
			}
		}
		return nil 
	}
 
	// 非叶子节点继续搜索子节点 
	idx := sort.SearchInts(node.keys, key)
	if idx < len(node.keys) && node.keys[idx] == key {
		// 精确匹配 
		return node.children[idx]
	} else if idx > 0 && node.keys[idx-1] == key {
		// 精确匹配 
		return node.children[idx-1]
	} else if idx < len(node.keys) {
		// 搜索中间位置 
		return node.children[idx].Search(key)
	} else {
		// 搜索右侧子节点 
		return node.children[idx-1].Search(key)
	}
}
 
func main() {
	root := NewBTreeNode(false)
	root.Insert(5)
	root.Insert(8)
	root.Insert(3)
	root.Insert(10)
	root.Insert(1)
 
	// 查找元素 
	fmt.Println(root.Search(8)) // 返回非叶子节点 
	fmt.Println(root.Search(6)) // 返回nil 
 
	// 在叶子节点上插入新元素 
	leaf := NewBTreeNode(true)
	leaf.Insert(7)
	leaf.Insert(9)
 
	// 将新叶子节点添加到根节点 
	root.children[1].children = append(root.children[1].children, leaf)
}

在这个例子中，BTreeNode 结构体包含了子节点数组、关键字数组以及一个标志位表示该节点是否为叶子节点。插入和搜索操作都利用了Go的切片和排序函数来简化逻辑。

由于B树的最小度数t影响了树的形态和性能，所以在创建新节点时，我们通常会设定一个最小度数，并在插入新元素时保证节点的子节点数量和关键字数量满足这个最小度数的要求。在上述代码中，我们没有显式地检查最小度数，但可以根据需要添加相应的逻辑。

智谱清言：

B树不允许最小度数t=1的原因是，这将导致B树失去平衡，并且无法保证所有的操作（如插入、删除和查找）都能在对数时间内完成。当t=1时，每个节点只能有一个子节点，这意味着在插入或删除操作时，节点的关键字数量可能会超过t-1个，从而违反B树的定义。此外，当t=1时，树的高度会变得非常高，这将导致磁盘I/O操作的次数增加，从而降低性能。

以下是一个使用Go语言实现的简单B树节点结构：

package main
import (
	"fmt"
)
type BTreeNode struct {
	keys   []int
	children []*BTreeNode
}
type BTree struct {
	root *BTreeNode
	t int
}
func NewBTree(t int) *BTree {
	return &BTree{
		root:    NewNode(t),
		t:       t,
	}
}
func NewNode(t int) *BTreeNode {
	return &BTreeNode{
		keys:   make([]int, 0, t),
		children: make([]*BTreeNode, 0, t+1),
	}
}
func (n *BTreeNode) Insert(key int) {
	// 在这里实现插入操作
}
func (n *BTreeNode) Delete(key int) {
	// 在这里实现删除操作
}
func (n *BTreeNode) Search(key int, index int) *BTreeNode {
	// 在这里实现查找操作
}
func main() {
	t := 3
	btree := NewBTree(t)
	// 在这里添加、删除或查找操作
	fmt.Println(btree)
}

请注意，这个代码只是一个简单的B树节点结构实现，没有实现所有的B树操作。你可以根据需要添加插入、删除和查找等操作的实现。

天工：

在B树中，最小的度（t）被定义为一个节点中键的最小数量。度为1的B树意味着每个节点最多只有一个键和两个子节点。这样的结构非常接近二叉搜索树，并且没有利用多路搜索树能够提供的并行性和平衡性优势。

B树设计的目的是优化磁盘I/O操作，特别是在数据库和文件系统中存储大量数据时。一个节点包含多个键可以减少树的高度，从而减少访问根节点到叶子节点所需的磁盘I/O次数。如果B树的度是1，树的高度将会很高，这将增加查找、插入和删除操作的成本。

此外，当B树的度是1时，它将失去其设计中的许多优化特性，例如：

1.平衡性：B树通过确保所有叶子节点都在同一层来保持平衡，这对于保持操作效率至关重要。度为1的B树无法保证平衡。

2.填充因子：B树设计有较高的填充因子，这意味着节点可以存储更多的键，减少了树的大小和深度。度为1的B树填充因子接近二叉树，远低于理想的B树。

3.磁盘I/O效率：B树的度越高，每个节点就能存储更多的信息，因此访问任何给定数据所需的磁盘I/O次数就越少。

由于这些原因，B树通常要求最小度大于1，以充分利用其设计优势。

以下是一个简单的Go语言示例代码，展示了一个B树的基本结构和插入操作：

package main
import (
	"fmt"
)
type Node struct {
	keys    []int
	children []*Node
}
type BTree struct {
	root *Node
	degree int
}
func newNode(degree int) *Node {
	return &Node{
		keys:    make([]int, 0, degree-1),
		children: make([]*Node, 0, degree),
	}
}
func (bt *BTree) insert(key int) {
	if bt.root == nil {
		bt.root = newNode(bt.degree)
	}
	bt.insertRecursive(key, bt.root)
}
func (bt *BTree) insertRecursive(key int, node *Node) {
	i := len(node.keys)
	for i > 0 && node.keys[i-1] > key {
		i--
	}
	node.keys = append(node.keys, 0)
	copy(node.keys[i+1:], node.keys[i:])
	node.keys[i] = key
	if len(node.keys) < bt.degree {
		return
	}
	midKey := node.keys[(bt.degree-1)/2]
	leftChild := newNode(bt.degree)
	rightChild := newNode(bt.degree)
	leftHalfKeys := make([]int, 0, bt.degree-1)
	rightHalfKeys := make([]int, 0, bt.degree-1)
	j := 0
	for i, key := range node.keys[:(bt.degree-1)/2] {
		if key < midKey {
			leftHalfKeys = append(leftHalfKeys, key)
			leftChild.children[j] = node.children[i]
			j++
		}
	}
	k := 0
	for i, child := range node.children[(bt.degree-1)/2+1:] {
		rightHalfKeys = append(rightHalfKeys, child.keys...)
		rightChild.children[k] = child.children[i]
		k++
	}
	leftChild.keys = leftHalfKeys
	rightChild.keys = rightHalfKeys
	node.keys = node.keys[(bt.degree-1)/2+1:]
	node.children = node.children[(bt.degree-1)/2+1:]
	bt.insertRecursive(midKey, &BTree{root: leftChild})
	bt.insertRecursive(midKey, &BTree{root: rightChild})
}
func main() {
	bt := BTree{degree: 3} // 假设我们使用的是3阶B树
	bt.insert(10)
	bt.insert(5)
	bt.insert(15)
	bt.insert(3)
	bt.insert(8)
	// 打印树的根节点键
	fmt.Println("Root keys:", bt.root.keys)
}

这个代码示例创建了一个简单的B树实现，其中degree是B树的最小度，这里设置为3。insert函数用于向树中插入新的键，而insertRecursive函数负责递归地插入键并在必要时进行分裂。注意，此代码未处理所有可能的边界情况和错误检查，仅用于演示目的。

chatgpt：

在B树中，不允许最小度数t=1的原因是为了维持树的平衡性和高效性。如果最小度数为1，会导致以下问题：

  1. 插入和删除操作复杂度：当节点的最小度数为1时，每个节点只能容纳一个关键字和两个孩子指针。这将导致B树变得非常稀疏，并且需要频繁地进行节点的分裂和合并操作。插入和删除操作需要沿着从根节点到叶子节点的路径进行调整和更新，而这样频繁的分裂和合并会大大增加插入和删除操作的复杂度。

  2. 空间利用率低：当最小度数为1时，每个节点只能容纳一个关键字和两个孩子指针，这意味着很多节点都会有较少的关键字。相比之下，更大的最小度数可以提供更好的空间利用率，并减少存储开销。

如果要使用Go语言实现一个B树结构，你可以按照以下步骤进行：

首先，在Go语言中定义一个B树结点类型（Node），包含关键字（Key）和对子结点（Child）的引用。

然后，实现B树插入操作（Insert）来将新元素插入到正确位置，并保持树的平衡性。

接下来，实现B树查找操作（Search）来搜索指定关键字对应的元素。

最后，实现B树删除操作（Delete）来删除指定关键字对应的元素，并进行必要的调整以保持树的平衡性。

注意，具体的代码实现细节可能会有所不同，需要根据具体需求和数据结构设计进行相应调整。这里只是一个简单示例，你可以参考该示例编写自己的代码。

kimi：

B树中不允许最小度数 ( t = 1 ) 的原因主要基于B树的设计原则和性能要求。B树是为了优化磁盘I/O操作而设计的，它通过维护节点的最小度数来保证树的平衡性，从而减少查找、插入和删除操作时所需的磁盘访问次数。如果最小度数 ( t = 1 )，则B树将失去其平衡性，并且无法有效减少磁盘访问次数。以下是几个关键点：

  1. 平衡性：B树通过最小度数 ( t ) 来保证每个内部节点至少有 ( t ) 个子节点，这有助于保持树的平衡性。

  2. 磁盘I/O：B树设计用于减少磁盘I/O次数。如果 ( t = 1 )，那么每个节点将只能有一个子节点，这将导致树变得非常高，从而增加查找路径上的磁盘访问次数。

  3. 空间浪费：B树的节点通常对应于磁盘块。如果 ( t = 1 )，那么每个节点将只有一个子节点，这将导致大量的空间浪费，因为磁盘块的大部分空间将不被使用。

  4. 性能：B树的性能优势在于其能够保持较低的树高。如果 ( t = 1 )，树的高度将增加，导致性能下降。

尽管Go语言不是讨论B树不允许最小度数 ( t = 1 ) 的直接原因，但我们可以编写Go语言代码来展示B树的基本结构和插入操作，以及为什么在实际应用中选择一个大于1的最小度数是有意义的。

以下是Go语言中B树的一个简单实现示例：

package main

import (
	"fmt"
)

const (
	minDegree = 2 // B树的最小度数
)

type BTreeNode struct {
	data    []int
	isLeaf  bool
	children []*BTreeNode
	parent  *BTreeNode
}

func NewBTreeNode(data []int, isLeaf bool) *BTreeNode {
	return &BTreeNode{
		data:    data,
		isLeaf:  isLeaf,
		children: make([]*BTreeNode, 0),
	}
}

func (node *BTreeNode) Insert(data int) {
	if len(node.data) == (2*minDegree-1) && !node.isLeaf {
		// 如果节点满了，需要分裂
		// 这里省略了分裂的具体实现
		panic("node is full, need to split")
	}

	// 插入数据的代码，这里省略
	// ...
}

func main() {
	root := NewBTreeNode([]int{}, false)
	// 插入数据的示例
	// root.Insert(10)
	// root.Insert(20)
	// ...
	
	fmt.Println("B-Tree created with minimum degree:", minDegree)
}

在这个Go语言实现中，我们定义了 BTreeNode 结构体来表示B树中的节点。每个节点包含了数据、是否为叶子节点的标志、子节点数组和指向父节点的指针。Insert 方法用于向节点中插入数据。如果节点已满（即数据数量达到 ( 2t - 1 )），则需要进行分裂操作，这里我们使用 panic 来简化实现。

请注意，这个代码示例仅用于展示B树的基本结构，并没有实现完整的B树逻辑，包括节点分裂、合并和查找操作。在实际应用中，B树的实现会更加复杂，并且需要考虑磁盘I/O优化。

混元：

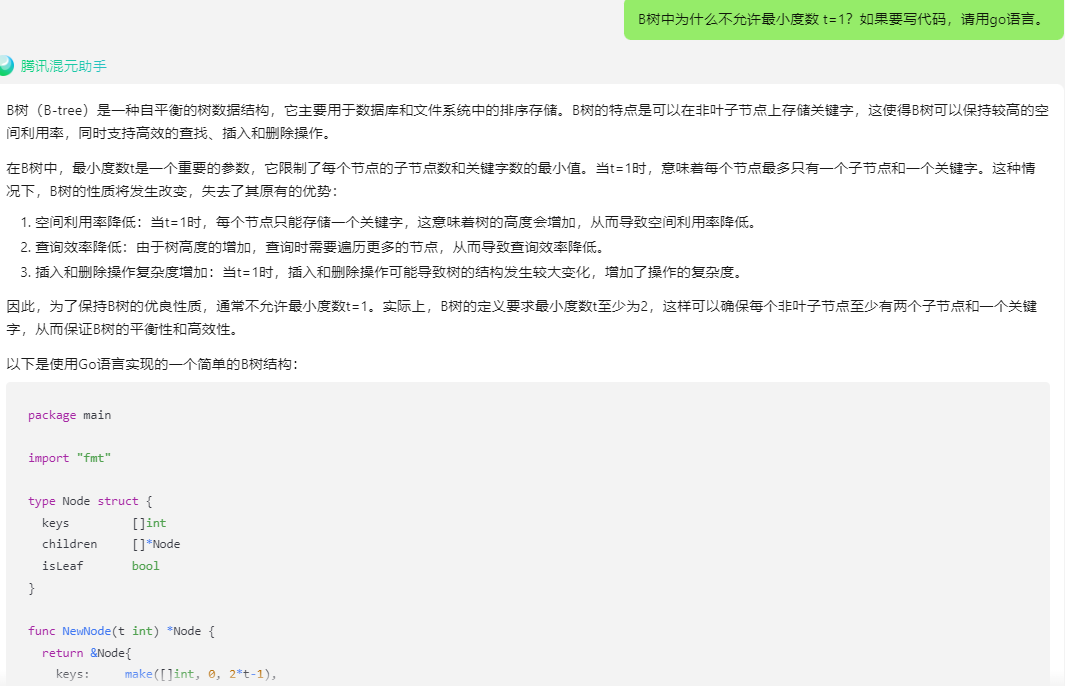
B树（B-tree）是一种自平衡的树数据结构，它主要用于数据库和文件系统中的排序存储。B树的特点是可以在非叶子节点上存储关键字，这使得B树可以保持较高的空间利用率，同时支持高效的查找、插入和删除操作。

在B树中，最小度数t是一个重要的参数，它限制了每个节点的子节点数和关键字数的最小值。当t=1时，意味着每个节点最多只有一个子节点和一个关键字。这种情况下，B树的性质将发生改变，失去了其原有的优势：

  1. 空间利用率降低：当t=1时，每个节点只能存储一个关键字，这意味着树的高度会增加，从而导致空间利用率降低。

  2. 查询效率降低：由于树高度的增加，查询时需要遍历更多的节点，从而导致查询效率降低。

  3. 插入和删除操作复杂度增加：当t=1时，插入和删除操作可能导致树的结构发生较大变化，增加了操作的复杂度。

因此，为了保持B树的优良性质，通常不允许最小度数t=1。实际上，B树的定义要求最小度数t至少为2，这样可以确保每个非叶子节点至少有两个子节点和一个关键字，从而保证B树的平衡性和高效性。

以下是使用Go语言实现的一个简单的B树结构：

package main

import "fmt"

type Node struct {
	keys         []int
	children     []*Node
	isLeaf       bool
}

func NewNode(t int) *Node {
	return &Node{
		keys:     make([]int, 0, 2*t-1),
		children: make([]*Node, 0, 2*t),
		isLeaf:   true,
	}
}

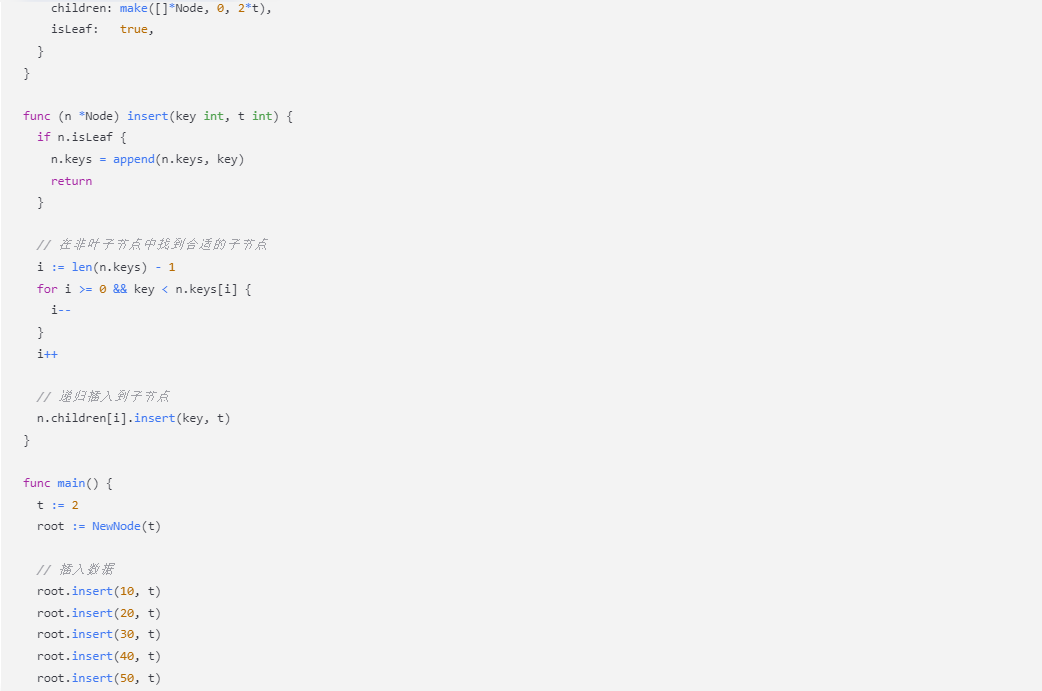
func (n *Node) insert(key int, t int) {
	if n.isLeaf {
		n.keys = append(n.keys, key)
		return
	}

	// 在非叶子节点中找到合适的子节点
	i := len(n.keys) - 1
	for i >= 0 && key < n.keys[i] {
		i--
	}
	i++

	// 递归插入到子节点
	n.children[i].insert(key, t)
}

func main() {
	t := 2
	root := NewNode(t)

	// 插入数据
	root.insert(10, t)
	root.insert(20, t)
	root.insert(30, t)
	root.insert(40, t)
	root.insert(50, t)

	// 打印结果
	fmt.Println("B树：")
	printTree(root, t)
}

func printTree(n *Node, t int) {
	if n == nil {
		return
	}

	for _, key := range n.keys {
		fmt.Print(key, " ")
	}
	fmt.Println()

	for _, child := range n.children {
		printTree(child, t)
	}
}

请注意，这个示例代码仅实现了B树的基本结构和插入操作，并没有实现B树的分裂和合并操作。在实际应用中，需要根据B树的规则实现这些操作以保持树的平衡。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1617794.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

openGauss学习笔记-269 openGauss性能调优-TPCC性能调优测试指导-数据库服务端及客户端绑核

openGauss学习笔记-269 openGauss性能调优-TPCC性能调优测试指导-数据库服务端及客户端绑核

文章目录 openGauss学习笔记-269 openGauss性能调优-TPCC性能调优测试指导-数据库服务端及客户端绑核269.1 安装openGauss数据库269.2 停止数据库269.3 使用gs_guc工具修改数据库端口、IP等269.4 使用gs_guc工具设置如下参数269.5 执行如下命令以绑核方式启动服务端数据库269.6…
阅读更多...
4月23日 C++day1

4月23日 C++day1

阅读更多...
在线教程丨刘强东数字人首秀交易额破5千万！用GeneFace++ 生成实时说话数字人

在线教程丨刘强东数字人首秀交易额破5千万！用GeneFace++ 生成实时说话数字人

近日&#xff0c;京东创始人刘强东化身「采销东哥 AI 数字人」&#xff0c;在京东家电家居和超市的采销直播间开启了自己的直播首秀。此次直播活动观看人次超 2 千万&#xff0c;交易总额超 5 千万&#xff0c;充分彰显了AI 数字人在电商直播领域的巨大潜力。 「采销东哥」亮相…
阅读更多...
SwiftUI 5.0（iOS 17.0）触摸反馈“震荡波”与触发器模式趣谈

SwiftUI 5.0（iOS 17.0）触摸反馈“震荡波”与触发器模式趣谈

概览 要想创作出一款精彩绝伦的 App&#xff0c;绚丽的界面和灵动的动画并不是唯一吸引用户的要素。有时我们还希望让用户真切的感受到操作引发的触觉反馈&#xff0c;直击使用者的灵魂。 所幸的是新版 SwiftUI 原生提供了实现触觉震动反馈的机制。在介绍它之后我们还将进一步…
阅读更多...
prompt提示词：小红书爆款标题提示词，让AI 帮你生成吸睛的标题

prompt提示词：小红书爆款标题提示词，让AI 帮你生成吸睛的标题

目录 小红书爆款标题提示词效果展示&#xff1a;提示词&#xff1a; 小红书爆款标题提示词 一篇文章若缺少了吸引人的标题&#xff0c;就如同失去了灵魂的躯壳&#xff0c;失去了与读者心灵相通的桥梁&#xff0c;上次发表了一篇小红书爆款文案生成助手 提示词&#xff0c;大家…
阅读更多...
Linux之安装Nginx

Linux之安装Nginx

目录 传送门前言一、快速安装二、反向代理语法1、基本语法2、location语法1. 基本语法2. 匹配规则3. 修饰符4. 权重5. 嵌套location6. 其他指令7.案例 三、配置反向代理 传送门 SpringMVC的源码解析&#xff08;精品&#xff09; Spring6的源码解析&#xff08;精品&#xff0…
阅读更多...
食用油5G智能工厂数字孪生可视化平台，推进食品制造业数字化转型

食用油5G智能工厂数字孪生可视化平台，推进食品制造业数字化转型

食用油5G智能工厂数字孪生可视化平台&#xff0c;推进食品制造业数字化转型。在食用油产业中&#xff0c;数字化转型已成为提升生产效率、优化供应链管理、确保产品质量和满足消费者需求的关键。食用油5G智能工厂数字孪生可视化平台作为这一转型的重要工具&#xff0c;正在推动…
阅读更多...
【来自理工科的独有浪漫-给crush一朵夏天的雪花】--对于有限差分法的理解

【来自理工科的独有浪漫-给crush一朵夏天的雪花】--对于有限差分法的理解

目录 有限差分法相关参考资料先上手看代码&#xff0c;然后理解数理概念有限差分法的理解Q: 什么是有限差分法&#xff1f; 代码中涉及的知识点1. 划分网格对于求解二维偏微分方程的作用2. 临近点对于求解偏微分方程的作用3. 有限差分方法中的中心差分公式 总结 写在前面&#…
阅读更多...
喜报 | 一致认可！擎创科技连续6年获“鑫智奖”专家推荐TOP10优秀解决方案

喜报 | 一致认可！擎创科技连续6年获“鑫智奖”专家推荐TOP10优秀解决方案

为展示金融企业数据管理和数据平台智能化转型成果&#xff0c;分享大数据和人工智能在风控、营销、产品、运营等场景的落地实践&#xff0c;探讨“金融科技数据智能”的创新应用和未来发展&#xff0c;在全球金融专业人士协会的支持下&#xff0c;金科创新社主办了“鑫智奖第六…
阅读更多...
Apple II首席设计师为中国家庭设计，鹿客指脉锁S6 Max引领科技美学

Apple II首席设计师为中国家庭设计，鹿客指脉锁S6 Max引领科技美学

智能门锁设计正在步入一个科技与艺术交织的美学时代。鹿客科技认为&#xff0c;智能门锁的设计理念是将锁视为人类与仿生形状之间的接口&#xff0c;将门视为几何建筑的一部分&#xff0c;产品设计应该通过提供诱人且用户友好的“触摸和感觉”来传达这种转变。 鹿客近日发布的最…
阅读更多...
（C语言入门）数组

（C语言入门）数组

目录 什么是数组&#xff1f; 数组&#xff1a; 数组的使用&#xff1a; 数组的初始化&#xff1a; 数组名&#xff1a; 数组案例&#xff1a; 一维数组的最大值&#xff1a; 一维数组的逆置&#xff1a; 数组和指针&#xff1a; 通过指针操作数组元素&#xff1a; …
阅读更多...
springCloud集成activiti5.22.0流程引擎

springCloud集成activiti5.22.0流程引擎

springCloud集成activiti5.22.0流程引擎 点关注不迷路&#xff0c;欢迎再访&#xff01; 精简博客内容&#xff0c;尽量已行业术语来分享。 努力做到对每一位认可自己的读者负责。 帮助别人的同时更是丰富自己的良机。 小编最近工作需要涉及到流程&#xff0c;由于网络上5.22版…
阅读更多...
AD--SSL卸载--单向认证和双向认证

AD--SSL卸载--单向认证和双向认证

一.SSL卸载单向认证 1.添加SSL证书 2.添加SSL卸载策略 由于是测试模拟环境&#xff0c;有些效果表现不出来&#xff0c;配置不了卸载策略 3.起虚拟服务&#xff0c;服务类型选择https或者ssl ,选择SSL卸载策略 实验效果&#xff1a;打开网页进入AD抓包发现&#xff0c;客户端和…
阅读更多...
MySQL及SQL语句

MySQL及SQL语句

SQL语句 数据库相关概念数据查询语言&#xff08;DQL&#xff09;基本查询数据类型条件查询多表查询子查询 数据操作语言&#xff08;DML&#xff09;数据定义语言&#xff08;DDL&#xff09;数据控制语言&#xff08;DCL&#xff09;MySQL数据库约束视图练习题 数据库相关概念…
阅读更多...
8【PS作图】画一个“像素云朵”

8【PS作图】画一个“像素云朵”

选择64*128像素大小&#xff0c;横向画布 选择“油漆桶”工具&#xff0c;“容差”调整为0&#xff0c;取消“锯齿”&#xff0c;勾选“连续的”&#xff0c;这样方便后续上色&#xff0c;并且边缘都是像素风格的锯齿状 点击画布&#xff0c;变成蓝色天空 画云朵&#xff0c;首…
阅读更多...
win10环境中设置java开机自启动

win10环境中设置java开机自启动

1 、jdk环境确认 在开始设置Java开机启动之前&#xff0c;确保你的计算机已经安装了Java开发环境&#xff08;JDK&#xff09;。如果没有安装&#xff0c;你可以从Oracle官方网站下载并安装最新的Java开发工具包。 2、准备好jar程序 确认jar程序可以正常运行。 3、编写批处…
阅读更多...
【InternLM】大模型的评测——OpenCompass

【InternLM】大模型的评测——OpenCompass

1. OpenCompass简介 1.1 基本介绍 大模型开源开放评测体系 “司南” (OpenCompass2.0)由上海人工智能实验室科学家团队发布&#xff0c;用于为大语言模型、多模态模型等提供一站式评测服务。其主要特点如下&#xff1a; 开源可复现&#xff1a;提供公平、公开、可复现的大模型…
阅读更多...
聊聊实际工作中设计模式的使用

聊聊实际工作中设计模式的使用

一直想在CSDN上写一篇关于软件设计模式的文章&#xff0c;草稿打了好久&#xff0c;但很长时间都没有想好该如何写&#xff0c;主要有几点考虑&#xff1a; 1、市面上同类的介绍实在太多了。正所谓第一个能够把美女比喻成鲜花的人是天才&#xff0c;第二个还这么说的是庸才&…
阅读更多...
Kotlin语法入门-类与对象(6)

Kotlin语法入门-类与对象(6)

Kotlin语法入门-类与对象(6) 文章目录 Kotlin语法入门-类与对象(6)六、类与对象1、声明和调用2、get和set3、init函数初始化4、constructor构造函数4.1、主构造函数4.2、二级构造函数4.3、多个构造函数4.4、省略主构造函数并写了次构造函数 5、类的继承与重写5.1、继承5.2、继承…
阅读更多...
【Tello无人机】无人机编队操作面板实现

【Tello无人机】无人机编队操作面板实现

为了方便进行无人机的编队演示&#xff0c;以及在各种场景下实现队形的灵活切换&#xff0c;开发了一套专门的上位机控制平台。本文将重点介绍应用于tello无人机的编队操作面板及其核心功能。 操作面板页面 下图展示了操作面板&#xff0c;其中包含5种编队动作和3个可选位置设…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023