目录
- 有限差分法相关参考资料
- 先上手看代码,然后理解数理概念
- 有限差分法的理解
- Q: 什么是有限差分法?
- 代码中涉及的知识点
- 1. 划分网格对于求解二维偏微分方程的作用
- 2. 临近点对于求解偏微分方程的作用
- 3. 有限差分方法中的中心差分公式
- 总结
写在前面:炎炎夏日,用代码给你的crush送上一朵雪花吧。一起感受一下偏微分方程的浪漫。
有限差分法相关参考资料
以下资料为我学习的来源:
链接1: 中科院的有限差分法的详细解释课程
链接2: 论文:Modeling and numerical simulations of dendritic crystal growth
链接3: 知乎 对应上文解释 代码来源!
先上手看代码,然后理解数理概念
要注释
from numpy import *
# 定义参数
# 本模块对应的知识点1【划分网格对于求解二维偏微分方程的作用】
# 网格的行数,列数以及时间迭代的总步数
M, N, K = 300, 300, 4000
# 空间时长步长
Dx, Dy, Dt = 0.01, 0.01, 1e-5
# 材料参数
# 包含物理和材料属性参数,包括相场动力学时间常数、各向异性能量强度、相场方向依赖的强度、晶格取向因子、参考取向、界面宽度参数、温度敏感度、平衡温度和热耦合系数。
# 为求解数学物理方程中的控制物理生成物形态的参数
tau = 3e-4
eps_bar = 0.01
sigma = 0.02
J = 4.
theta_0 = 0.2
alpha = 0.9
gamma = 10.
T_eq = 1.
kappa = 1.8
# 初始条件设置
p = zeros((M, N))
T = zeros((M, N))
# 半径为sqrt(5.0)的圆内,被视为初始固化区域的一部分,这部分我们认为相变已经完成,即雪花已经开始产生
for i in range(M):
for j in range(N):
if (i - M/2)**2 + (j - N/2)**2 < 5.0:
p[i, j] = 1.0 # 已经开始产生相变,设为1
# 定义二维拉普拉斯算子(扩散、波动等现象的偏微分方程时非常重要的算子)
# 知识点2【临近点对于求解偏微分方程的作用】
# 知识点3【有限差分方法中的中心差分公式】
def Lap(p):
# 提取内部和邻近点的值
p_i_j = delete(delete(p, [0, -1], axis=0), [0, -1], axis=1)
p_im_j = delete(delete(p, [0, -1], axis=0), [-1,-2], axis=1)
p_ip_j = delete(delete(p, [0, -1], axis=0), [0, 1], axis=1)
p_i_jm = delete(delete(p, [0, -1], axis=1), [0, 1], axis=0)
p_i_jp = delete(delete(p, [0, -1], axis=1), [-1,-2], axis=0)
# 计算拉普拉斯算子,使用限差分方法中的中心差分公式
Lap_p = (p_im_j + p_ip_j + p_i_jm + p_i_jp - 4*p_i_j)/Dx**2
# 处理边界条件
Lap_pj = vstack((Lap_p[0,:], Lap_p, Lap_p[-1,:]))
return hstack((Lap_pj[:,0].reshape(N,1), Lap_pj, Lap_pj[:,-1].reshape(N,1)))
# 计算相场p的演化,这里可以看知乎的那篇推导原文,十分详细
def Phase_field(p, T):
theta = arctan2(gradient(p, Dy, axis=1), gradient(p, Dx, axis=0))
eps = eps_bar * (1. + sigma * cos(J * (theta - theta_0)))
g = -eps * eps_bar * sigma * J * sin(J * (theta - theta_0)) * gradient(p, Dy, axis=1)
h = -eps * eps_bar * sigma * J * sin(J * (theta - theta_0)) * gradient(p, Dx, axis=0)
m = alpha/pi * arctan(gamma * (T_eq - T))
# 结合界面能、界面动力学以及热效应等因素,形成相场的演化方程。
term_1 = - p*(p - 1.)*(p - 0.5 + m)
term_2 = - gradient(g, Dx, axis=0)
term_3 = gradient(h, Dy, axis=1)
term_4 = eps**2 * Lap(p)
p_ev = Dt / tau * (term_1 + term_2 + term_3 + term_4)
return p + p_ev
# 计算温度场T的演化
def Temp(T, p_new, p_old):
T_ev = Dt*Lap(T) + kappa*(p_new - p_old)
return T + T_ev
# 相场更新
p_hist = []
T_hist = []
p_old = p; T_old = T
for t_step in range(K):
p_new = Phase_field(p_old, T_old)
T_new = Temp(T_old, p_new, p_old)
p_old = p_new
T_old = T_new
if t_step % 50 == 0:
p_hist.append(p_new)
T_hist.append(T_new)
print('step finished:', t_step,'/',str(K))
有限差分法的理解
Q: 什么是有限差分法?
在我的理解里,有限差分法就是对于微分方程/偏微分方程求解的一种数理方法,本质就是把对于微分的求解转化为求解大量代数方程组。转化的过程本质上是一种近似。
举一个最简单的例子,假设我们有一个连续的函数,我们想要计算它在某个特定点的导数。为了使用有限差分法,我们将函数在该点附近进行离散化处理。首先,我们选择一个很小的步长,称为差分间距(finite difference interval)或网格间距(grid spacing)。然后,在该点的左右两侧选择一些离散点。我们根据这些离散点的函数值来估计函数在该点的导数。具体来说,我们可以使用中心差分(central difference)或前向差分(forward difference)等方法来计算导数。
代码中涉及的知识点
1. 划分网格对于求解二维偏微分方程的作用
网格划分是数值方法中处理偏微分方程的基础,它将连续的物理空间离散化成有限的点集,使得连续问题可以在计算机上用离散方式处理。
在这段代码中,M和N定义了在两个空间维度上的网格点数,这决定了模型的空间分辨率。网格点越多,空间分辨率越高,模拟结果越精确,但计算量也越大。
2. 临近点对于求解偏微分方程的作用
将求解域进行离散化是偏微分方程的关键。如果是一维条件下进行计算求解,我们可以在脑子里想象一条线,知道后一个点,就可以根据初始值迭代。如果是二维条件下进行计算求解,那么每个点周围的临近点应该会有四个,在脑子里把他们连起来,那么会形成一个矩形,使用任何四个结点的值就可以算出最后一个。这就是为什么二维中心差分公式会使用如下表达式迭代:
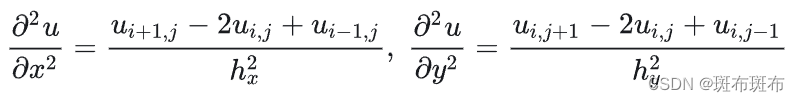
此外,代码中的空间步长(Dx, Dy)和时间步长(Dt)决定了数值模拟的精度和稳定性。步长越小,理论上数值解越接近真实解,但计算时间也更长。时间步长还与数值方法的稳定性有关。特别是对于显式方法,如果步长过大,可能导致数值解的不稳定或发散。
3. 有限差分方法中的中心差分公式
中心差分因为相比前向差分/后向差分多一重精度,因此,经常被用来作为差分公式的公式。
Lap§函数计算二维拉普拉斯算子,这是通过有限差分的中心差分公式实现的。拉普拉斯算子在物理中描述了某个量(如温度、压力等)的空间扩散。在边界处采用简单的延伸处理,这相当于假设边界外的值等于边界上的值(Neumann边界条件)。
总结
通过学习使用代码产生雪花,我对于有限差分法有了进一步的理解。
另外标题是吸引大家一起学习有限差分法的,不建议给crush发雪花代码,带他/她去哈尔滨看雪效果更好。