1.移动零
移动零
思路:
利用双指针算法
cur:从左往右扫描数组,遍历数组
dest:处理好的区间包括dest
dest初始化为-1,因为刚开始dest前应该没有非零元素。
即将非零元素移到dest之前即可
class Solution {
public:
void moveZeroes(vector<int>& nums) {
for(int cur = 0, dest = -1; cur < nums.size(); cur++)
{
if(nums[cur]) //非零元素
{
swap(nums[++dest], nums[cur]);
}
}
}
};2.复写零
复写零
思路:
要注意的是从“异地”操作,优化为“就地”操作。即题目要求是只能在就地操作,那我们就可以先尝试模拟在异地操作使用双指针算法,然后进行优化到就地双指针。
就地进行模拟时,应该从前往后还是从后往前,我们发现从前往后会覆盖掉我们需要的内容,所以我们要从后往前开始复写。
但又有个问题,我们并不知道最后要复写的内容是哪个!
所以我们要先从前开始寻找最后一个需要复写的元素
这时我们发现一个特例,这就是边界情况。dest走到了n的位置
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int cur = 0, dest = -1, n = arr.size();
//寻找最后一个需要复写的元素
while(cur < n)
{
if(arr[cur]) dest++;
else dest+=2;
if(dest >=n-1) break;
cur++;
}
//处理边界情况
if(dest == n)
{
arr[n - 1] = 0;
cur--;
dest-=2;
}
//从后往前复写
while(cur >= 0)
{
if(arr[cur])
{
arr[dest--] = arr[cur];
}
else
{
arr[dest--] = 0;
arr[dest--] = 0;
}
cur--;
}
}
};3.快乐数
快乐数

思路:利用快慢指针解决
class Solution {
public:
int bitsum(int n)
{
int sum = 0;
while(n)
{
int r = n % 10;
sum += r * r;
n /= 10;
}
return sum;
}
bool isHappy(int n) {
int slow = n, fast = bitsum(n);
while(slow != fast)
{
slow = bitsum(slow);
fast = bitsum(bitsum(fast));
}
return slow == 1;
}
};4.盛最多水的容器
盛最多水的容器
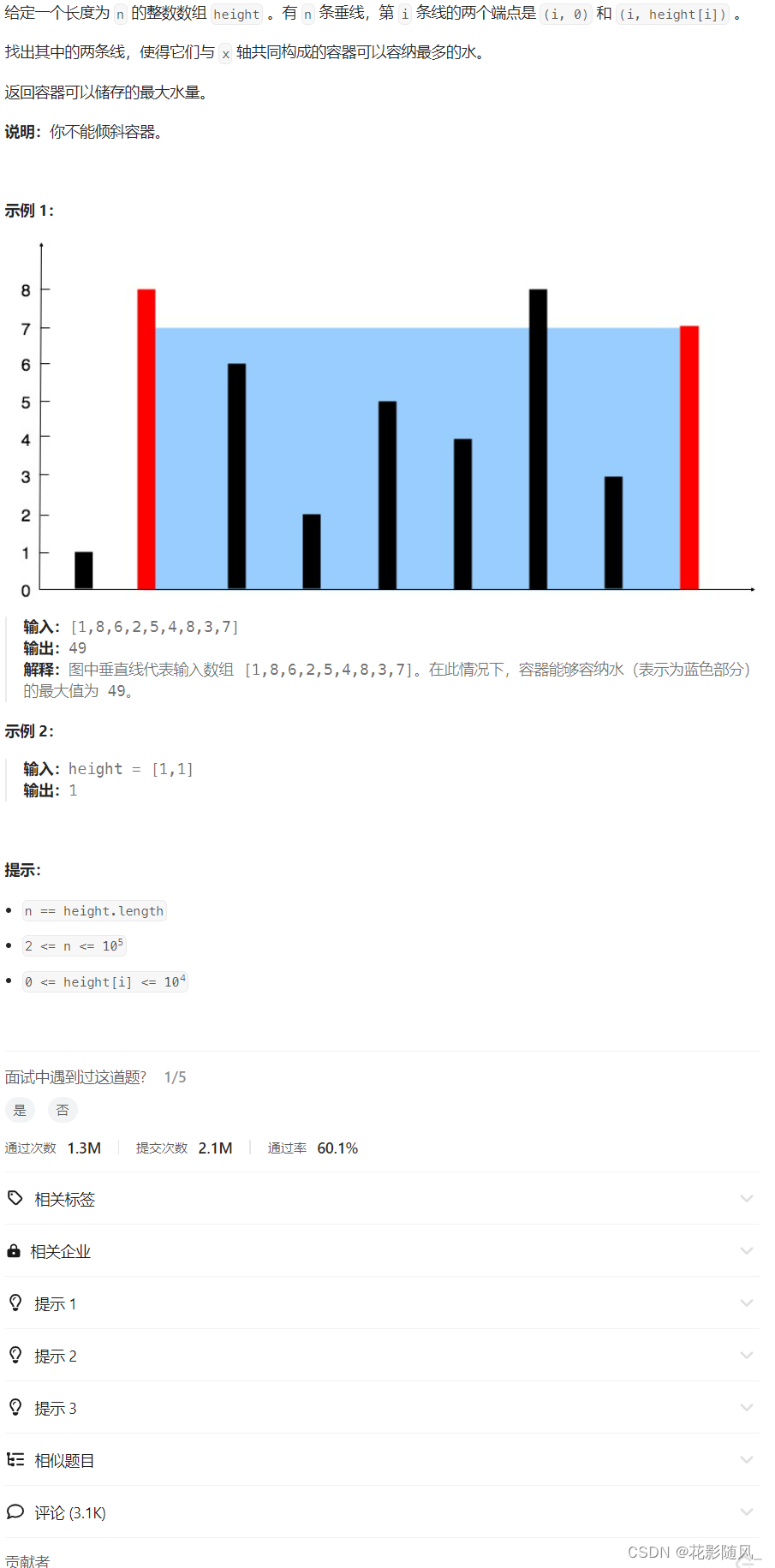
思路:利用对撞指针解决,强度单调性
class Solution {
public:
int maxArea(vector<int>& height) {
int left = 0, right = height.size() - 1;
int ret = 0;
while(left < right)
{
int v = min(height[left], height[right]) * (right - left);
ret = max(ret, v);
if(height[left] < height[right]) left++;
else right--;
}
return ret;
}
};5.有效三角形的个数
有效三角形的个数
思路:
对撞指针,利用单调性
class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(), nums.end());
int ret = 0, n = nums.size();
for(int i = n - 1; i >= 2; i--)
{
int left = 0, right = i - 1;
while(left < right)
{
if(nums[left] + nums[right] > nums[i])
{
ret+=(right - left), right--;
}
else
{
left++;
}
}
}
return ret;
}
};6.和为s的两个数
查找总价格为目标值的商品

思路:
对撞指针,单调性
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
int left = 0, right = price.size() - 1;
while(left < right)
{
if(price[left] + price[right] < target)
{
left++;
}
else if(price[left] + price[right] > target)
{
right--;
}
else
{
return {price[left], price[right]};
}
}
return {-1, -1};
}
};7.三数之和
三数之和

思路:
对撞指针 ,使用二数之和思想
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> ret;
sort(nums.begin(), nums.end());
int n = nums.size();
for(int i = 0; i < n; ) // i是固定数a
{
if(nums[i] > 0) break;//常数级优化
int left = i + 1, right = n - 1, target = -nums[i];//寻找和等于target的两数
while(left < right)
{
int sum = nums[left] + nums[right];
if(sum < target)
{
left++;
}
else if(sum > target)
{
right--;
}
else
{
ret.push_back({nums[i], nums[left], nums[right]});
//不漏
left++;
right--;
//去重 left right
while(left < right && nums[left] == nums[left - 1]) left++;
while(left < right && nums[right] == nums[right + 1]) right--;
}
}
//去重i
i++;
while(i < n && nums[i] == nums[i - 1]) i++;
}
return ret;
}
};8.四数之和
四数之和

思路:
使用三数之和思想
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> ret;
sort(nums.begin(), nums.end());
int n = nums.size();
for(int i = 0; i < n;)
{
for(int j = i + 1; j < n;)
{
int left = j + 1, right = n - 1;
//防止t数据溢出,开long long
long long t = (long long)target - nums[i] - nums[j];
while(left < right)
{
if(nums[left] + nums[right] < t) left++;
else if(nums[left] + nums[right] > t) right--;
else{
ret.push_back({nums[i], nums[j], nums[left], nums[right]});
//不漏
left++, right--;
//去重 left 和 right
while(left < right && nums[left] == nums[left - 1]) left++;
while(left < right && nums[right] == nums[right + 1]) right--;
}
}
//去重j
j++;
while(j < n && nums[j] == nums[j - 1]) j++;
}
//去重i
i++;
while(i < n && nums[i] == nums[i - 1]) i++;
}
return ret;
}
};