基于 Deep Learning (2017, MIT) 书总结了必要的概率知识
原blog 以及用到的Ipython notebook
文章目录
- 1 概述
- 2 知识
- 2.1 离散变量和概率质量函数(PMF)
- 2.2 连续变量和概率密度函数(PDF)
- 2.3 边缘概率
- 2.4 条件概率
- 2.5 条件概率的链式法则
- 2.6 独立性和条件独立性
- 2.7 期望、方差和协方差
- 2.8 常见概率分布
- 2.9 常见函数的有用性质
- 2.10 贝叶斯定理
- 3 应用问题
1 概述
概率论是表示不确定性陈述的数学框架。在AI领域中,我们以两种主要方式使用概率论。首先,概率定律告诉我们AI系统应该如何推理,因此我们设计算法来计算或近似使用概率论得出的各种表达式。其次,我们可以使用概率和统计来理论上分析所提出的AI系统的行为。
2 知识
2.1 离散变量和概率质量函数(PMF)
对离散变量的概率分布可以用概率质量函数(PMF)来描述。
离散变量
x
x
x遵循分布
P
(
x
)
P(x)
P(x):
x
∼
P
(
x
)
\mathrm{x}\sim P(x)
x∼P(x)。
联合概率分布是许多变量的概率分布: P ( x = x , y = y ) P(\mathrm{x}=x, \mathrm{y}=y) P(x=x,y=y),或者 P ( x , y ) P(x,y) P(x,y)。
PMF的特性:
- P P P的定义域必须是 x \mathrm{x} x的所有可能状态的集合。
- 对于 ∀ x ∈ x \forall x\in \mathrm{x} ∀x∈x, 0 ≤ P ( x ) ≤ 1 0\leq P(x) \leq 1 0≤P(x)≤1。
- ∑ x ∈ x P ( x ) = 1 \sum_{x\in \mathrm{x}}P(x)=1 ∑x∈xP(x)=1。
均匀分布: P ( x = x i ) = 1 K P(\mathrm{x}=x_i)=\dfrac{1}{K} P(x=xi)=K1。
2.2 连续变量和概率密度函数(PDF)
概率密度函数(PDF)用于描述连续随机变量的概率分布。PDF的函数 p p p必须满足以下特性:
- p p p的定义域是 x \mathrm{x} x的所有可能状态的集合。
- 对于 ∀ x ∈ x \forall x\in \mathrm{x} ∀x∈x, p ( x ) ≥ 0 p(x)\geq0 p(x)≥0。注意不要求 p ( x ) ≤ 1 p(x)\leq 1 p(x)≤1。
- ∫ p ( x ) d x = 1 \int p(x)dx=1 ∫p(x)dx=1。
PDF不是概率,PDF与PMF不同,PDF可以大于1。离散和连续随机变量的定义方式不同。对于连续随机变量,必要条件是 ∫ p ( x ) d x = 1 \int p(x)dx=1 ∫p(x)dx=1。PDF不直接给出特定状态的概率,而是给出落入 δ x \delta x δx的无穷小区域内的概率,即 p ( x ) δ x p(x)\delta x p(x)δx。变量 x x x位于区间 [ a , b ] [a,b] [a,b]的概率由 ∫ [ a , b ] p ( x ) d x \int_{[a,b]}p(x)dx ∫[a,b]p(x)dx给出。
均匀分布 u ( x ; a , b ) = 1 b − a u(x;a,b)=\dfrac{1}{b-a} u(x;a,b)=b−a1, a a a和 b b b是区间的端点。分号表示参数化。 x x x是函数的参数, a a a和 b b b是参数。 x ∼ U ( a , b ) x\sim U(a,b) x∼U(a,b)表示 x x x遵循均匀分布。
2.3 边缘概率
对变量子集的概率分布称为边缘概率分布。例如,对于离散随机变量 x \mathrm{x} x和 y \mathrm{y} y,已知 P ( x , y ) P(\mathrm{x},\mathrm{y}) P(x,y),可以使用求和规则计算 P ( x ) P(\mathrm{x}) P(x): ∀ x ∈ x \forall x\in \mathrm{x} ∀x∈x, P ( x = x ) = ∑ y P ( x = x , y = y ) P(\mathrm{x}=x)=\sum_{y}P(\mathrm{x}=x, \mathrm{y}=y) P(x=x)=∑yP(x=x,y=y)。对于连续变量,需要使用积分而不是求和: p ( x ) = ∫ p ( x , y ) d y p(x)=\int p(x,y)dy p(x)=∫p(x,y)dy。
2.4 条件概率
计算某个事件发生的概率,已知某些其他事件已发生。这是条件概率。 P ( y = y ∣ x = x ) P(\mathrm{y}=y|\mathrm{x}=x) P(y=y∣x=x), x = x \mathrm{x}=x x=x是条件。可以使用公式 P ( y = y ∣ x = x ) = P ( y = y , x = x ) P ( x = x ) P(\mathrm{y}=y|\mathrm{x}=x)=\dfrac{P(\mathrm{y}=y,\mathrm{x}=x)}{P(\mathrm{x}=x)} P(y=y∣x=x)=P(x=x)P(y=y,x=x)来计算。
条件概率仅在 P ( x = x ) > 0 P(\mathrm{x}=x)>0 P(x=x)>0时定义。我们不能计算条件是从不发生事件的条件概率。
2.5 条件概率的链式法则
任何多个随机变量的联合概率分布可以分解为对单个变量的条件分布,这称为链式法则或乘法规则。 P ( x ( 1 ) , … , x ( n ) ) = P ( x ( 1 ) ) Π i = 2 n P ( x ( i ) ∣ x ( 1 ) , … , x ( i − 1 ) ) P(\mathrm{x}^{(1)},\ldots,\mathrm{x}^{(n)})=P(\mathrm{x}^{(1)})\Pi_{i=2}^nP(\mathrm{x}^{(i)}|\mathrm{x}^{(1)},\ldots,\mathrm{x}^{(i-1)}) P(x(1),…,x(n))=P(x(1))Πi=2nP(x(i)∣x(1),…,x(i−1))。
一些例子:
P
(
a
,
b
,
c
)
=
P
(
a
∣
b
,
c
)
P
(
b
,
c
)
P(a,b,c)=P(a|b,c)P(b,c)
P(a,b,c)=P(a∣b,c)P(b,c);
P
(
b
,
c
)
=
P
(
b
∣
c
)
P
(
c
)
P(b,c)=P(b|c)P(c)
P(b,c)=P(b∣c)P(c);
P
(
a
,
b
,
c
)
=
P
(
a
∣
b
,
c
)
P
(
b
∣
c
)
P
(
c
)
P(a,b,c)=P(a|b,c)P(b|c)P(c)
P(a,b,c)=P(a∣b,c)P(b∣c)P(c)。
2.6 独立性和条件独立性
如果 x x x和 y y y是独立的( x ⊥ y x\perp y x⊥y),则: ∀ x ∈ x , y ∈ y , p ( x = x , y = y ) = p ( x = x ) p ( y = y ) \forall x\in \mathrm{x}, y \in \mathrm{y}, p(\mathrm{x}=x, \mathrm{y}=y)=p(\mathrm{x}=x)p(\mathrm{y}=y) ∀x∈x,y∈y,p(x=x,y=y)=p(x=x)p(y=y)。
给定随机变量
z
z
z,如果
x
x
x和
y
y
y在条件
z
z
z下独立(
x
⊥
y
∣
z
x\perp y|z
x⊥y∣z),则:
∀
x
∈
x
,
y
∈
y
,
z
∈
z
,
p
(
x
=
x
,
y
=
y
,
z
=
z
)
=
p
(
x
=
x
∣
z
=
z
)
p
(
y
=
y
∣
z
=
z
)
\forall x\in \mathrm{x}, y\in \mathrm{y}, z\in \mathrm{z}, p(\mathrm{x}=x, \mathrm{y}=y, \mathrm{z}=z)=p(\mathrm{x}=x|\mathrm{z}=z)p(\mathrm{y}=y|\mathrm{z}=z)
∀x∈x,y∈y,z∈z,p(x=x,y=y,z=z)=p(x=x∣z=z)p(y=y∣z=z)
2.7 期望、方差和协方差
期望
对于离散变量: E x ∼ P [ f ( x ) ] = ∑ x P ( x ) f ( x ) \mathbb{E}_{\mathrm{x}\sim P}[f(x)]=\sum_{x}P(x)f(x) Ex∼P[f(x)]=∑xP(x)f(x)。
对于连续变量: E x ∼ P [ f ( x ) ] = ∫ P ( x ) f ( x ) d x \mathbb{E}_{\mathrm{x}\sim P}[f(x)]=\int{P(x)f(x)}dx Ex∼P[f(x)]=∫P(x)f(x)dx。
期望是线性的: E x [ α f ( x ) + β g ( x ) ] = α E x [ f ( x ) ] + β E x [ g ( x ) ] \mathbb{E}_{\mathrm{x}}[\alpha f(x)+\beta g(x)]=\alpha \mathbb{E}_{\mathrm{x}}[f(x)] + \beta \mathbb{E}_{\mathrm{x}}[g(x)] Ex[αf(x)+βg(x)]=αEx[f(x)]+βEx[g(x)]
方差
V a r ( f ( x ) ) = E [ ( f ( x ) − E [ f ( x ) ] ) 2 ] Var(f(x))=\mathbb{E}[(f(x)-\mathbb{E}[f(x)])^2] Var(f(x))=E[(f(x)−E[f(x)])2]
当方差很小时, f ( x ) f(x) f(x)的值会聚集在其期望值附近。方差的平方根称为标准差。
协方差
协方差给出两个值之间线性相关的程度,以及这些变量的尺度:
C
o
v
(
f
(
x
)
,
g
(
y
)
)
=
E
[
(
f
(
x
)
−
E
[
f
(
x
)
]
)
(
g
(
y
)
−
E
[
g
(
y
)
]
)
]
Cov(f(x),g(y))=\mathbb{E}[(f(x)-\mathbb{E}[f(x)])(g(y)-\mathbb{E}[g(y)])]
Cov(f(x),g(y))=E[(f(x)−E[f(x)])(g(y)−E[g(y)])]
协方差的绝对值较高意味着这些值变化很大,并且同时远离各自的均值。正号表示两个变量倾向于同时取相对较高的值。负号表示一个变量取得高值,另一个变量取得低值,反之亦然。
协方差与相关的关系:
- 独立变量的协方差为零。非零协方差的变量是相关的。
- 独立性是比零协方差更强的要求。两个变量可以相关,但协方差为零。
随机向量
x
∈
R
n
\mathbf{x}\in \mathbb{R}^n
x∈Rn的协方差矩阵是一个
n
×
n
n\times n
n×n矩阵:
C
o
v
(
x
)
i
,
j
=
C
o
v
(
x
i
,
x
j
)
Cov(\mathbf{x})_{i,j}=Cov(\mathbf{x}_i,\mathbf{x}_j)
Cov(x)i,j=Cov(xi,xj)
协方差的对角线元素给出了方差:
C
o
v
(
x
i
,
x
i
)
=
V
a
r
(
x
i
)
Cov(\mathbf{x}_i,\mathbf{x}_i)=Var(\mathbf{x}_i)
Cov(xi,xi)=Var(xi)。
2.8 常见概率分布
在机器学习中有几个有用的概率分布。
伯努利分布
分布在单个二进制随机变量上。特性:
- P ( x = 1 ) = ϕ P(\mathbf{x}=1)=\phi P(x=1)=ϕ, p ( x = 0 ) = 1 − ϕ p(\mathbf{x}=0)=1-\phi p(x=0)=1−ϕ
- P ( x = x ) = ϕ x ( 1 − ϕ ) 1 − x P(\mathbf{x}=x)=\phi^x(1-\phi)^{1-x} P(x=x)=ϕx(1−ϕ)1−x
- E x [ x ] = ϕ \mathbb{E}_{\mathbf{x}}[\mathbf{x}]=\phi Ex[x]=ϕ
- V a r x ( x ) = ϕ ( 1 − ϕ ) Var_\mathbf{x}(\mathbf{x})=\phi(1-\phi) Varx(x)=ϕ(1−ϕ)
多项式分布
或分类分布,是具有 k k k个不同状态的单个离散变量的分布。
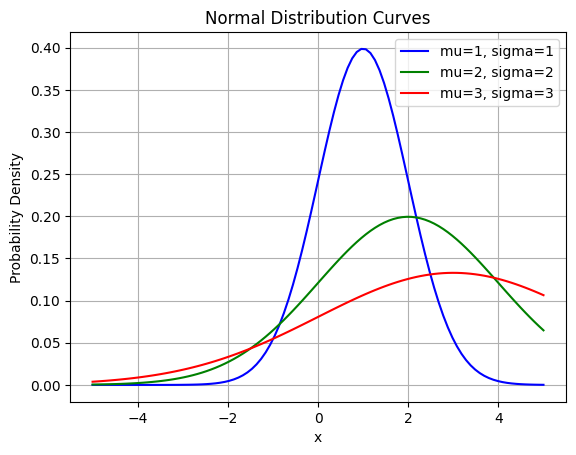
高斯分布
或正态分布:
N
(
x
;
μ
,
σ
2
)
=
1
2
π
σ
2
exp
(
−
1
2
σ
2
(
x
−
μ
)
2
)
\mathcal{N}(x;\mu,\sigma^2)=\sqrt{\dfrac{1}{2\pi \sigma^2}}\exp(-\dfrac{1}{2\sigma^2(x-\mu)^2})
N(x;μ,σ2)=2πσ21exp(−2σ2(x−μ)21)
- μ \mu μ给出了中心峰值的坐标,这也是分布的均值: E [ x ] = μ \mathbb{E}[\mathbf{x}]=\mu E[x]=μ
- 分布的标准差: σ \sigma σ
- 方差: σ 2 \sigma^2 σ2
指数和拉普拉斯分布
指数分布: p ( x ; λ ) = λ 1 x ≥ 0 exp ( − λ x ) p(x;\lambda)=\lambda 1_{x\geq 0} \exp(-\lambda x) p(x;λ)=λ1x≥0exp(−λx)
对于所有负值的 x x x,概率为零。
拉普拉斯分布: L a p l a c e ( x ; μ , γ ) = 1 2 γ exp ( − ∣ x − μ ∣ γ ) Laplace(x;\mu,\gamma)=\dfrac{1}{2\gamma}\exp(-\dfrac{|x-\mu|}{\gamma}) Laplace(x;μ,γ)=2γ1exp(−γ∣x−μ∣)
狄拉克分布和经验分布
狄拉克分布: p ( x ) = δ ( x − μ ) p(x)=\delta (x-\mu) p(x)=δ(x−μ)
经验分布: p ^ ( x ) = 1 m ∑ i = 1 m δ ( x − x ( i ) ) \hat{p}(x)=\dfrac{1}{m}\sum_{i=1}^m\delta(x-x^{(i)}) p^(x)=m1∑i=1mδ(x−x(i))
2.9 常见函数的有用性质
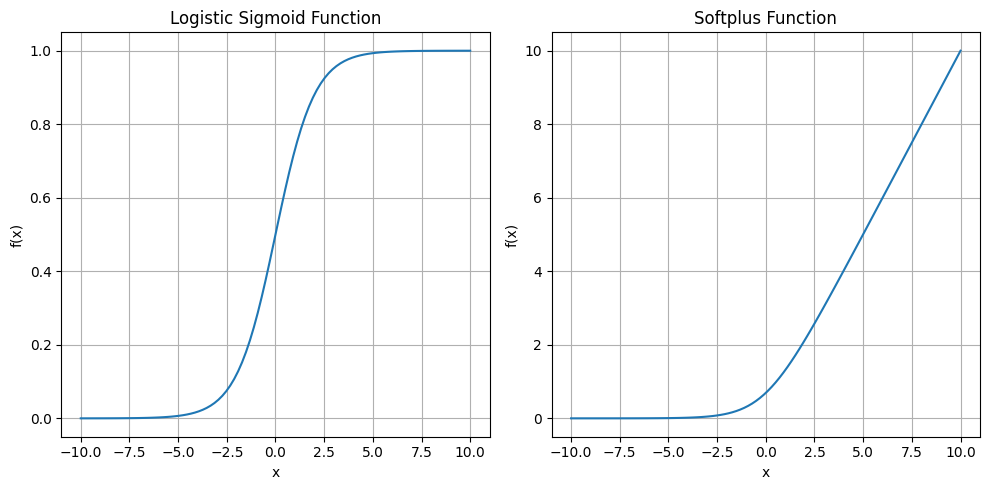
Logistic sigmoid 函数
σ ( x ) = 1 1 + exp ( − x ) \sigma(x)=\dfrac{1}{1+\exp(-x)} σ(x)=1+exp(−x)1
它通常用于生成 Bermoulli 分布的 ϕ \phi ϕ 参数。当其参数非常正或负时,sigmoid 函数饱和,意味着函数变得非常平坦,对其输入的微小变化不敏感。
Softplus 函数
ζ ( x ) = log ( 1 + exp ( x ) ) \zeta(x)=\log(1+\exp(x)) ζ(x)=log(1+exp(x))
该函数可用于生成正态分布的 β \beta β 或 σ \sigma σ 参数。
重要性质
- σ ( x ) = exp ( x ) exp ( x ) + 1 \sigma(x)=\dfrac{\exp(x)}{\exp(x)+1} σ(x)=exp(x)+1exp(x)
- d d x σ ( x ) = σ ( x ) ( 1 − σ ( x ) ) \dfrac{d}{dx}\sigma(x)=\sigma(x)(1-\sigma(x)) dxdσ(x)=σ(x)(1−σ(x))
- 1 − σ ( x ) = σ ( − x ) 1-\sigma(x)=\sigma(-x) 1−σ(x)=σ(−x)
- log σ ( x ) = − ζ ( − x ) \log\sigma(x) = -\zeta(-x) logσ(x)=−ζ(−x)
- d d x ζ ( x ) = σ ( x ) \dfrac{d}{dx}\zeta(x)=\sigma (x) dxdζ(x)=σ(x)
- ∀ x ∈ ( 0 , 1 ) , σ − 1 ( x ) = log ( x 1 − x ) \forall x\in (0,1), \sigma^{-1}(x)=\log(\dfrac{x}{1-x}) ∀x∈(0,1),σ−1(x)=log(1−xx)
- ∀ x > 0 , ζ − 1 ( x ) = log ( exp ( x ) − 1 ) \forall x > 0, \zeta^{-1}(x)=\log (\exp(x)-1) ∀x>0,ζ−1(x)=log(exp(x)−1)
- ζ ( x ) = ∫ − ∞ x σ ( y ) d y \zeta(x)=\int_{-\infin}^{x}\sigma(y)dy ζ(x)=∫−∞xσ(y)dy
- ζ ( x ) − ζ ( − x ) = x \zeta (x) - \zeta(-x) = x ζ(x)−ζ(−x)=x
2.10 贝叶斯定理
P ( x ∣ y ) = P ( x ) P ( y ∣ x ) P ( y ) P(x|y)=\dfrac{P(x)P(y|x)}{P(y)} P(x∣y)=P(y)P(x)P(y∣x)
通过 P ( y ∣ x ) P(y|x) P(y∣x) 计算 P ( x ∣ y ) P(x|y) P(x∣y),注意 P ( y ) = ∑ x P ( y ∣ x ) P ( x ) P(y)=\sum_xP(y|x)P(x) P(y)=∑xP(y∣x)P(x)。贝叶斯定理是一种在拥有一些信息情况下计算某件事发生可能性的方法。
3 应用问题
问题1:有一个公平的硬币(一面是正面,一面是反面)和一个不公平的硬币(两面都是反面)。你随机选择一个硬币,抛掷5次,观察到全部5次都是反面。你抛的是不公平的硬币的几率是多少?
定义
U
U
U 为抛出不公平硬币的情况;
F
F
F 表示抛出公平硬币。
5
T
5T
5T 表示我们连续抛出5次正面的事件。
我们知道
P
(
U
)
=
P
(
F
)
=
0.5
P(U) = P(F) = 0.5
P(U)=P(F)=0.5,需要求解
P
(
U
∣
5
T
)
P(U|5T)
P(U∣5T)。
P
(
U
∣
5
T
)
=
P
(
5
T
∣
U
)
P
(
U
)
P
(
5
T
)
P(U|5T) = \dfrac{P(5T|U)P(U)}{P(5T)}
P(U∣5T)=P(5T)P(5T∣U)P(U)
=
1
∗
0.5
P
(
5
T
∣
U
)
P
(
U
)
+
P
(
5
T
∣
F
)
P
(
F
)
=\dfrac{1*0.5}{P(5T|U)P(U)+P(5T|F)P(F)}
=P(5T∣U)P(U)+P(5T∣F)P(F)1∗0.5
=
0.5
1
∗
0.5
+
0.
5
5
∗
0.5
≈
0.97
=\dfrac{0.5}{1*0.5+0.5^5*0.5}\approx0.97
=1∗0.5+0.55∗0.50.5≈0.97
因此,选择了不公平硬币的概率约为97%。
问题2:你和你的朋友正在玩一个游戏。你们两个将继续抛硬币,直到序列 HH 或 TH 出现为止。如果先出现 HH,你赢。如果先出现 TH,你的朋友赢。每个人的获胜概率是多少?
P(HH 先出现而不是 TH) = P(前两次抛出 HH) = 1/4
P(TH 先出现而不是 HH) = P(首次为 T) + P(前两次为 HT) = 1/2 + 1/4 = 3/4
问题3:1000人中有1人患有一种特定的疾病,并且有一种检测方法,如果患有该疾病,检测正确率为98%。如果没有患病,检测错误率为1%。如果有人检测为阳性,他们患病的几率是多少?
P(D) = 1/1000 表示患有疾病的概率
P(H) = 1 - P(D) = 999/1000 表示健康的概率
P(P|D) = 98% 表示如果患有疾病,则检测为阳性的概率
P(P|H) = 1% 表示如果没有患病,则检测为阳性的概率
需要求解 P(D|P)
P ( D ∣ P ) = P ( P ∣ D ) P ( D ) P ( P ) P(D|P)=\dfrac{P(P|D)P(D)}{P(P)} P(D∣P)=P(P)P(P∣D)P(D) = 98 / 100 ∗ 1 / 1000 P ( P ∣ D ) P ( D ) + P ( P ∣ H ) P ( H ) = \dfrac{98/100*1/1000}{P(P|D)P(D) + P(P|H)P(H)} =P(P∣D)P(D)+P(P∣H)P(H)98/100∗1/1000 = 0.098 % 98 % ∗ 1 / 1000 + 1 % ∗ 999 / 1000 = \dfrac{0.098\%}{98\%*1/1000 + 1\% * 999/1000} =98%∗1/1000+1%∗999/10000.098% ≈ 8.94 % \approx 8.94\% ≈8.94%
因此,如果有人检测为阳性,则他们患病的概率约为0.0894或8.94%。