目录
题目一:
题目二:
题目三:
题目三:
题目四:
题目五:
题目六:
题目七:
题目八:
题目一:
题目:不创建临时变量,交换两个数。
思路:(方法一:交换律思想)
- 先将两个数相加赋值给num1,此时num1为两数之和
- 接着对赋值后的num1 - num2,即6-2,此时的结果就是一开始num1的值,赋值给num2此时num2存储了一开始num1的值
- 最后两数之和 - num2,可以得出一开始num2的值,赋值给num1,就完成交换
- 缺陷:可能溢出,当两个数太大时,相加可能超出整形大小
#include<stdio.h>
//不创建临时变了,交换两个数
int main()
{
int num1 = 4;
int num2 = 2;
printf("交换前:%d %d\n", num1, num2);
num1 = num1 + num2;
num2 = num1 - num2;
num1 = num1 - num2;
printf("交换后:%d %d\n", num1, num2);
return 0;
}思路:(方法二:异或操作符法)
- 异或的特殊性:
- 两个相同的数进行异或 == 0,因为异或是相同为0,相异为1.
- n^0 == n,为什么?因为0的二进制为32个0,则任何数的二进制要么为0要么1,当对应二进制位为0时,则为0,为1时,则为1,本质上没有改变。
- 异或支持交换律,如:3^5^3 == 5 等价于 3^3^5 == 5
#include<stdio.h>
//不创建临时变了,交换两个数
int main()
{
int num1 = 4;
int num2 = 2;
printf("交换前:%d %d\n", num1, num2);
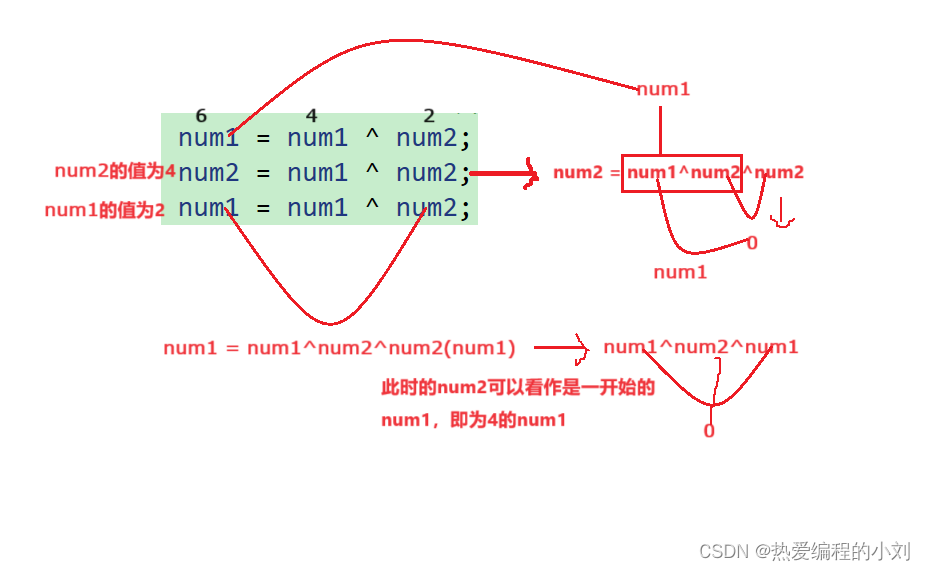
num1 = num1 ^ num2;
num2 = num1 ^ num2; //拆分成:num2 = num1^num2^num2 异或支持交换律,因此值为变化前的num1
num1 = num1 ^ num2; //拆分成:num1 = num1^num2^num2(num1),num2的值其实就是变化前的num1,
//因此值为变化前的num2
printf("交换后:%d %d\n", num1, num2);
return 0;
}
题目二:
题目:编写代码实现:求一个整数存储在内存中的二进制中1的个数。
思路1:
- 题目要求统计一个整数的二进制中有多少个1.
- 对该整数按位与上一个1即可。
- 按位与:对二进制进行操作,一个为0,结果为0,两个为1才为1.
- 因此对一个数按位与1,可以判断该数的最低位是否为1.
- 判断完之后对该数进行右移操作,移动1位,持续对最低位进行判断。
#include<stdio.h>
int main()
{
int n = 0;
scanf("%d", &n);
int count = 0;
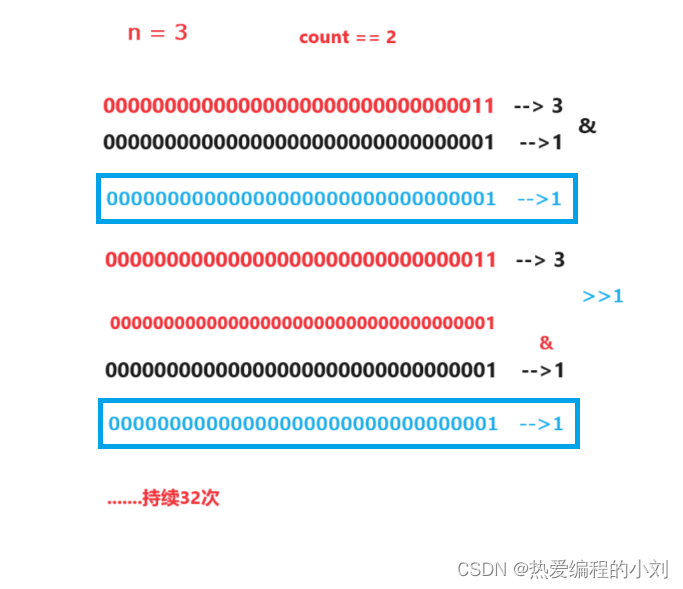
//循环32次是因为一个整数4字节,32比特,由32个二进制组成
for (int i = 0; i < 32; i++)
{
//n&1,判断最低位是否为1
if (n & 1)
{
count++;
}
//无论最低位是1还是0,均更新最低位,即右移
n = n >> 1;
}
printf("%d的二进制中有:%d个1\n", n, count);
return 0;
}
思路2:采用相邻的两个数进行按位与操作(非常高效)
- &:1个0都为0,两个1才为1
- res和res-1的二进制有什么区别?假设res==3
- res:....011;res-1:....010
- res&res-1结果:010,因此可以得出,一个res-1后,得到的二进制位将是res二进制最右侧的1变为0的二进制
- 再进行&操作后,就能得到res二进制位中将1个1变为0的二进制数
- 因此,只要不断的重复,当最后res变为0了,也就说明res中的1被全部去除
- 因此循环多少次,就代表res中1的个数
#include<stdio.h>
int main()
{
int n = 0;
scanf("%d", &n);
int count = 0;
while(n)
{
n = n & (n-1);
count++;
}
printf("%d的二进制中有:%d个1\n", n, count);
return 0;
}题目三:
题目:假设把一个数的二进制中某一位改为1,其它位不变
思路:
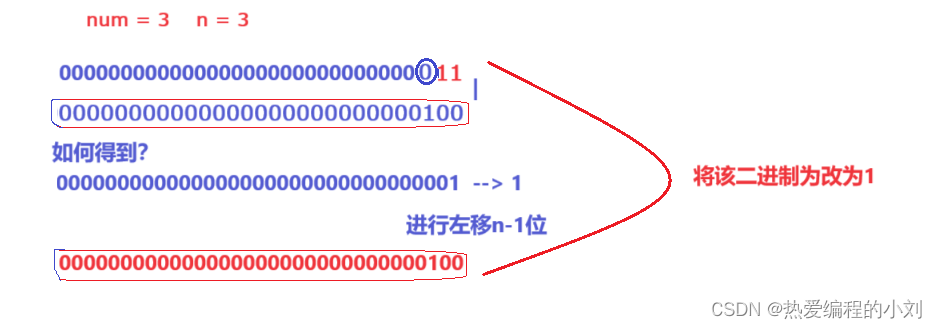
- 利用位操作符的特性,对该数的二进制中第n位进行按位或1操作,其它位均或0,则只会改变第n位上的二进制为1.
- 按位或:一个为1则为1,两个为0才为0.
- 对第n位按位或1,当第n位时1时,则为1,是0时,也为1.
- 如何得到这个二进制序列呢?通过对1左移n-1位。
#include <stdio.h>
int main()
{
int num = 0;
int n = 0;
scanf("%d %d", &num, &n);
//对num二进制中第n修改为1
num = num | (1 << n-1);
printf("%d\n", num);
return 0;
}
如果现在又想将该位改为0该怎么做?也就是对一个数的某个二进制为改为0
思路:
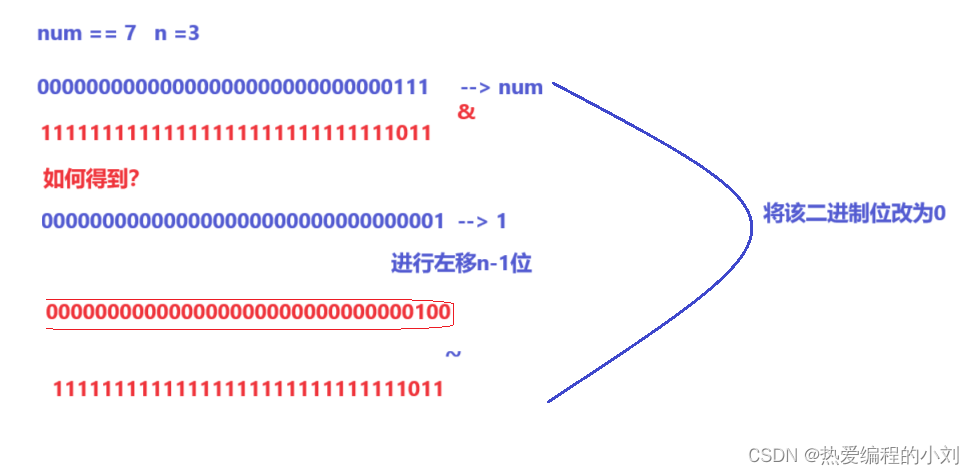
- 同样的,针对于二进制中的某一位,那对该位按位与0。
- 按位与:一个为0则为0,两个为1才为1。
- 如果该位是1,那按位与0则为0,如果该位是0,那按位与0也为0.
- 如何得到这个二进制序列呢?分为两步:
- 首先得到刚刚对某一位二进制改为1的二进制序列,对它进行取反操作。说简单点就是对1左移n-1位。
- 对该二进制序列按位取反操作。
#include <stdio.h>
int main()
{
int num = 0;
int n = 0;
scanf("%d %d", &num, &n);
//对num二进制中第n修改为1
num = num | (1 << n-1);
printf("将该位改为1:%d\n", num);
num = num & (~(1<<n-1));
printf("将该位改为0:%d\n", num);
return 0;
}
题目三:
题目:打印整数二进制的奇数位和偶数位
描述:获取一个整数二进制序列中所有的偶数位和奇数位,分别打印出二进制序列
思路:
- 获取一个数二进制位中的最低位:n & 1,能得出n的最低位是0还是1.
- 因此计算一个数二进制的偶数位和奇数位,只需要控制好每次按位与第几个二进制位就可以了。
- 奇数位:写得出高位中最后一个奇数位,即第31位,打印后,不断-2得到下一个奇数位,这就需要通过>>操作符了。
- 偶数位:同样的,写对第32位进行打印,再不断-2得到下一个偶数位。通过>>操作符。
#include <stdio.h>
int main()
{
int a = 2; //010
//获取二进制的偶数位
for (int i = 31; i >= 1; i-=2)
{
printf("%d ", (a >> i) & 1);
}
printf("\n");
//获取二进制的奇数位
for (int i = 30; i >= 0; i-=2)
{
printf("%d ", (a >> i) & 1);
}
return 0;
}题目四:
题目:两个整数二进制位不同个数_牛客题霸_牛客网 (nowcoder.com)
描述:
输入两个整数,求两个整数二进制格式有多少个位不同
输入描述:
两个整数
输出描述:
二进制不同位的个数
示例:
输入:22 33
输出:5
思路:
分为两部分:
- 对两个整数进行异或操作,因为异或的特点为:相同为0,相异为1。因此结果中二进制位1的个数就是不同的个数。
- 统计res中有几个1。
#include <stdio.h>
int Comp_func(int res)
{
//方法一:>>和&操作
//检查res中的二进制位有几个1,就是不同的个数
//res&1能得到最低位是0还是1,int32个二进制位,那就不断更新最低位进行&
//如何不断得到最低位呢?res>>i
int count = 0;
// for (int i=0; i<32; i++) {
// if ((res>>i)&1) {
// count++;
// }
// }
//方法二:利用&的特性,对两个相邻的数进行&操作(非常高效)
//&:1个0都为0,两个1才为1
//res和res-1的二进制有什么区别?假设res==3
//res:....011;res-1:....010
//res&res-1结果:010,因此可以得出,一个res-1后,得到的二进制位将是res二进制最右侧的1变为0的二进制
//再进行&操作后,就能得到res二进制位中将1个1变为0的二进制数
//因此,只要不断的重复,当最后res变为0了,也就说明res中的1被全部去除
//因此循环多少次,就代表res中1的个数
while (res) {
res = res & (res - 1);
count++;
}
return count;
}
int main() {
int a, b;
scanf("%d %d", &a, &b);
//a^b, 异或的特点:相同为0,相异为1
//a^b 后,相同的二进制位变为0,不同的变为1
int count = Comp_func(a ^ b);
printf("%d\n", count);
return 0;
}题目五:
题目:有序序列合并_牛客题霸_牛客网 (nowcoder.com)
描述:
输入两个升序排列的序列,将两个序列合并为一个有序序列并输出。
输入描述:输入包含三行
第一行包含两个正整数n, m,用空格分隔。n表示第二行第一个升序序列中数字的个数,m表示第三行第二个升序序列中数字的个数。
第二行包含n个整数,用空格分隔。
第三行包含m个整数,用空格分隔。
输出描述:输出为一行,输出长度为n+m的升序序列,即长度为n的升序序列和长度为m的升序序列中的元素重新进行升序序列排列合并。示例:
输入:
5 6
1 3 7 9 22
2 8 10 17 33 44
输出:
1 2 3 7 8 9 10 17 22 33 44
思路:
- 定义一个n+m大小的数组res
- 依次将n和m个整数输入到res中
- 对res进行冒泡排序
#include <stdio.h>
int main() {
int n = 0;
int m = 0;
scanf("%d %d", &n, &m);
int res[n+m];
for (int i = 0; i < n; i++) {
scanf("%d", &res[i]);
}
for (int i = n; i < n + m; i++) {
scanf("%d", &res[i]);
}
//排序,冒泡排序(升序)
//外层循环控制趟数,内存循环控制一趟的比较次数
for (int i = 0; i < n + m - 1; i++) {
for (int j = 0; j < n + m - 1 - i; j++) {
//升序
if (res[j] > res[j + 1]) {
int tmp = res[j];
res[j] = res[j + 1];
res[j + 1] = tmp;
}
}
}
for (int i = 0; i < n + m; i++) {
printf("%d ", res[i]);
}
}题目六:
题目:小乐乐走台阶_牛客题霸_牛客网 (nowcoder.com)
描述:
小乐乐上课需要走n阶台阶,因为他腿比较长,所以每次可以选择走一阶或者走两阶,那么他一共有多少种走法?
输入描述:输入包含一个整数n (1 ≤ n ≤ 30)
输出描述:输出一个整数,即小乐乐可以走的方法数。示例1:
输入:2
输出:2示例2:
输入:10
输出:89
思路:参考【C语言】青蛙跳台阶问题-CSDN博客
- n==1,只有1种跳法
- n==2,只有两种跳法
- n>2时,统计只走一阶台阶的方法 + 只走两阶的方法 == 总走法
- 递归
#include <stdio.h>
int function(int n)
{
//n为1时,只有1种走法
if (n == 1) {
return 1;
}
//n为2时,只有2种走法
if(n == 2) {
return 2;
}
//n>2时,统计只走一阶台阶的方法 + 只走两阶的方法 == 总走法
//需要用到递归
return function(n-1) + function(n-2);
}
int main()
{
//青蛙跳台阶问题
int n = 0;
scanf("%d", &n);
int count = function(n);
printf("%d\n", count);
return 0;
}题目七:
题目:变种水仙花_牛客题霸_牛客网 (nowcoder.com)
描述:
变种水仙花数 - Lily Number:把任意的数字,从中间拆分成两个数字,比如1461 可以拆分成(1和461),(14和61),(146和1),如果所有拆分后的乘积之和等于自身,则是一个Lily Number。
例如:
655 = 6 * 55 + 65 * 5
1461 = 1*461 + 14*61 + 146*1
求出 5位数中的所有 Lily Number。
输入描述:
无
输出描述:
一行,5位数中的所有 Lily Number,每两个数之间间隔一个空格。
思路:
运用%和/操作符,不断得到每个位数,如:n=12345,n%10==5,n/10=1234,进行相乘n%100=45,n/100=123,进行相乘.....依此类推
#include <stdio.h>
int main()
{
for (int i=10000; i<=99999; i++) {
//统计每个数拆分相乘后相加的值
int sum = 0;
for (int j=10; j<=10000; j*=10) {
sum += (i/j) * (i%j);
}
//判断sum是否等于i,如果是,则符合
if (sum == i) {
printf("%d ", i);
}
}
return 0;
}题目八:
题目:三角形判断_牛客题霸_牛客网 (nowcoder.com)
描述:
KiKi想知道已经给出的三条边a,b,c能否构成三角形,如果能构成三角形,判断三角形的类型(等边三角形、等腰三角形或普通三角形)。
输入描述:
题目有多组输入数据,每一行输入三个a,b,c(0<a,b,c<1000),作为三角形的三个边,用空格分隔。
输出描述:
针对每组输入数据,输出占一行,如果能构成三角形,等边三角形则输出“Equilateral triangle!”,等腰三角形则输出“Isosceles triangle!”,其余的三角形则输出“Ordinary triangle!”,反之输出“Not a triangle!”。
思路:
构成三角形的要求:两边之和大于第三边
三角形的类型:
- 等腰三角形:两边相等
- 等边三角形:三边相等
- 普通三角形:三边均不相等
#include <stdio.h>
int main() {
//三边
int a = 0;
int b = 0;
int c = 0;
while (scanf("%d %d %d", &a, &b, &c) == 3) {
//首先判断是否能构成三角形
if (a + b > c && a + c > b && b + c > a) {
//此时至少两条边相等,但也可能三条边相等
if (a == b || a == c || b == c) {
//三边相等-->等边三角形
if (a == b && b == c) {
printf("Equilateral triangle!\n");
}else { //等腰三角形
printf("Isosceles triangle!\n");
}
}
else {
printf("Ordinary triangle!\n");
}
} else {
printf("Not a triangle!\n");
}
}
return 0;
}