笔记-----BFS宽度优先搜索

对于BFS：宽搜第一次搜到就是最小值，并且基于迭代，不会爆栈。

Flood Fill 模型

如果直译的话就是：洪水覆盖，意思就是像是从一个点一圈圈的往外扩散，如果遇见能够连通的就扩散，如果遇见无法联通的就不去扩散，然后再去以扩散出去的点为起点再去扩散。

Flood Fill 可以实现在线性时间复杂度内找到某个点所在的连通块。

例题：

1.AcWing 1097. 池塘计数

农夫约翰有一片 $N * M$ 的矩形土地。

最近，由于降雨的原因，部分土地被水淹没了。

现在用一个字符矩阵来表示他的土地。

每个单元格内，如果包含雨水，则用”W”表示，如果不含雨水，则用”.”表示。

现在，约翰想知道他的土地中形成了多少片池塘。

每组相连的积水单元格集合可以看作是一片池塘。

每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。

请你输出共有多少片池塘，即矩阵中共有多少片相连的 ”W” 块。

输入格式
第一行包含两个整数 $N$ 和 $M$ 。
接下来 $N$ 行，每行包含 $M$ 个字符，字符为 ”W” 或 ”.” ，用以表示矩形土地的积水状况，字符之间没有空格。

输出格式
输出一个整数，表示池塘数目。

数据范围
$1 \leq N, M \leq 1000$

输入样例：

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.

输出样例：

每次取搜’W’，如果搜到了就去填充连通的所有的’W’并且标记上已经搜过了，然后每发现一滩新的水洼就让答案加1，此题较简单。并且曾经写过DFS的做法：题解博客

BFS:此处使用了便宜量和STL队列，并不和视频中相同

#include<iostream>
#include<queue>
using namespace std;
const int N = 1010;
const int dx[8] = { 0,0,1,-1,1,1,-1,-1 };
const int dy[8] = { 1,-1,0,0,1,-1,1,-1 };
#define pii pair<int,int>
#define x first
#define y second

int n, m;
char g[N][N];
bool st[N][N];

void bfs(int ix, int iy) {
	queue< pii >q;
	q.push({ ix,iy });
	st[ix][iy] = 1;

	while (q.size()) {
		auto t = q.front(); q.pop();
		for (int i = 0; i < 8; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];
			if (xx >= 0 && xx < n && yy >= 0 && yy < m && g[xx][yy] == 'W' && !st[xx][yy]) {
				q.push({ xx,yy });
				st[xx][yy] = 1;
			}
		}
	}
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);

	cin >> n >> m;
	for (int i = 0; i < n; i++)cin >> g[i];

	int cnt = 0;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			if (g[i][j] == 'W' && !st[i][j]) {
				bfs(i, j);
				cnt++;
			}
		}
	}

	cout << cnt;
	return 0;
}

2.AcWing 1098. 城堡问题

    1   2   3   4   5   6   7  
   #############################
 1 #   |   #   |   #   |   |   #
   #####---#####---#---#####---#
 2 #   #   |   #   #   #   #   #
   #---#####---#####---#####---#
 3 #   |   |   #   #   #   #   #
   #---#########---#####---#---#
 4 #   #   |   |   |   |   #   #
   #############################
           (图 1)

   #  = Wall   
   |  = No wall
   -  = No wall

   方向：上北下南左西右东。

图1是一个城堡的地形图。

请你编写一个程序，计算城堡一共有多少房间，最大的房间有多大。

城堡被分割成 $m * n$ 个方格区域，每个方格区域可以有 $0$ ~ $4$ 面墙。
注意：墙体厚度忽略不计。

输入格式
第一行包含两个整数 $m$ 和 $n$ ，分别表示城堡南北方向的长度和东西方向的长度。

接下来 $m$ 行，每行包含 $n$ 个整数，每个整数都表示平面图对应位置的方块的墙的特征。

每个方块中墙的特征由数字 $P$ 来描述，我们用 $1$ 表示西墙， $2$ 表示北墙， $4$ 表示东墙， $8$ 表示南墙， $P$ 为该方块包含墙的数字之和。

例如，如果一个方块的 P 为 $3$ ，则 $3 = 1 + 2$ ，该方块包含西墙和北墙。

城堡的内墙被计算两次，方块 $(1, 1)$ 的南墙同时也是方块 $(2, 1)$ 的北墙。

输入的数据保证城堡至少有两个房间。

输出格式
共两行，第一行输出房间总数，第二行输出最大房间的面积（方块数）。

数据范围
$1 \leq m, n \leq 50,$
$0 \leq P \leq 15$
输入样例：

4 7 
11 6 11 6 3 10 6 
7 9 6 13 5 15 5 
1 10 12 7 13 7 5 
13 11 10 8 10 12 13

输出样例：

5
9

此题并不困难，只是一个标准的Flood Fill模型题，只是输入的方式让人感到无语。

只要解决了读入的问题，那么这道题就做出来了。
首先题目读入的时候是读入的数字，并且观察题目的条件就会发现有含义的数字都是特殊的 $1 ， 2 ， 4 ， 8$ 分别是二进制的时候第一位，第二位，第三位，第四问为 $1$ 。那么只要读入之后，在后续BFS的过程中不再以传统的判断字符的方式来判定是否能走，而是改为读数字的二进制的位数是否为1来判断就好了，这里使用基础课讲过的lowbit()算法来处理。

并且这里要注意，偏移量要和题目给出的顺序来定。
因为后续遍历取偏移量的时候，如果我们读到了第一位是0，那么就要往西走，其他的方向要另行判定，如果偏移量乱定的话就会乱走。

再注意：编程里面的坐标轴和数学里是不一样的。以下是定偏移量时考虑的坐标轴。

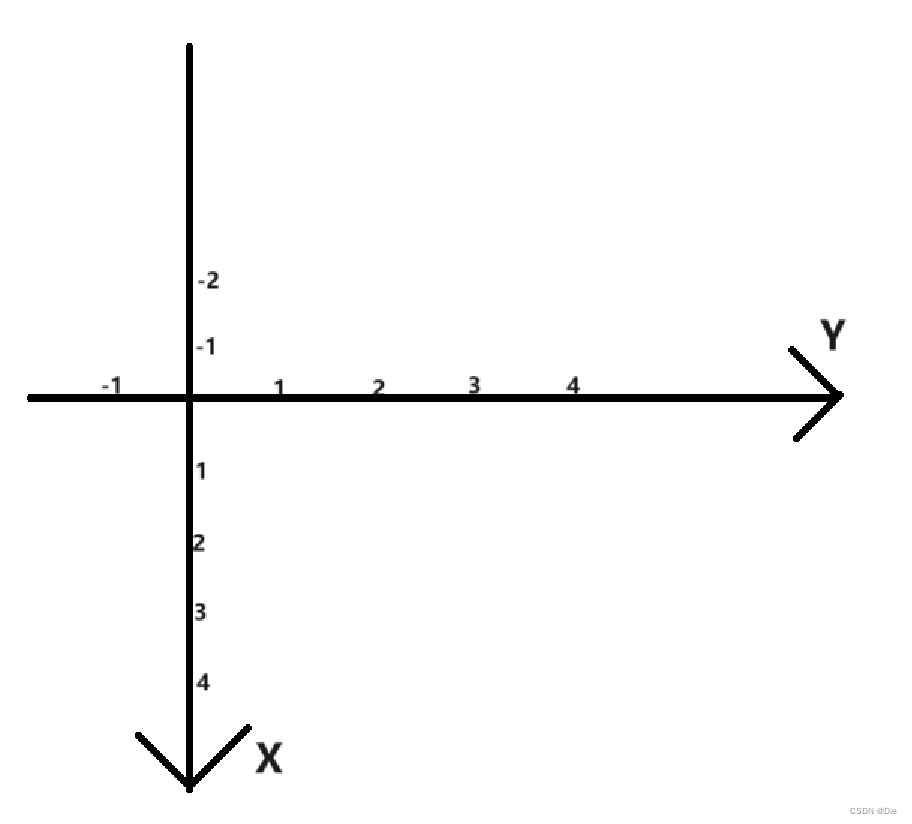
#include<iostream>
#include<queue>
using namespace std;
const int N = 55;

const int dx[4] = { 0,-1,0,1 };	/*注意这里对偏移量的定义，要严格按照题目给出的西，北，东，南的顺序来*/
const int dy[4] = { -1,0,1,0 };	

#define pii pair<int,int>
#define x first
#define y second

int n, m;
int g[N][N];
bool st[N][N];

int bfs(int ix, int iy) {
	queue<pii>q;
	int s = 0;
	q.push({ ix,iy });
	st[ix][iy] = 1;

	while (q.size()) {
		auto t = q.front();
		s++;	//每次出队，说明有一个空地
		q.pop();

		for (int i = 0; i < 4; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];

			//这里g[t.x][t.y] >> i & 1代表寻找当前i这一位是不是一
			//i为0，第1为是1，说明西边有墙，i为1时，第二位为1，说明北边有墙，以此类推
			if (xx >= 0 && xx<n && yy >= 0 && yy<m && !st[xx][yy] && !(g[t.x][t.y]>>i & 1)) {
				q.push({ xx,yy });
				st[xx][yy] = 1;
			}
		}
	}
	return s;
}

int main() {
	cin >> n >> m;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			cin >> g[i][j];
		}
	}

	int cnt = 0;
	int res = 0;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			if (!st[i][j]) {
				res = max(res, bfs(i, j));
				cnt++;
			}
		}
	}

	cout << cnt << endl;
	cout << res << endl;

	return 0;
}

3.AcWing 1106. 山峰和山谷

FGD小朋友特别喜欢爬山，在爬山的时候他就在研究山峰和山谷。

为了能够对旅程有一个安排，他想知道山峰和山谷的数量。

给定一个地图，为FGD想要旅行的区域，地图被分为 $n \times n$ 的网格，每个格子 $(i, j)$ 的高度 $w (i, j)$ 是给定的。

若两个格子有公共顶点，那么它们就是相邻的格子，如与 $(i, j)$ 相邻的格子有 $(i - 1, j - 1), (i - 1, j), (i - 1, j + 1), (i, j - 1), (i, j + 1), (i + 1, j - 1), (i + 1, j), (i + 1, j + 1)$ 。

我们定义一个格子的集合 $S$ 为山峰（山谷）当且仅当：

$S$ 的所有格子都有相同的高度。
$S$ 的所有格子都连通。
对于 $s$ 属于 $S$ ，与 $s$ 相邻的 $s'$ 不属于 $S$ ，都有 $w s > w s'$ （山峰），或者 $w s < w s'$ （山谷）。

如果周围不存在相邻区域，则同时将其视为山峰和山谷。

你的任务是，对于给定的地图，求出山峰和山谷的数量，如果所有格子都有相同的高度，那么整个地图即是山峰，又是山谷。

输入格式
第一行包含一个正整数 $n$ ，表示地图的大小。
接下来一个 $n \times n$ 的矩阵，表示地图上每个格子的高度 $w$ 。

输出格式
共一行，包含两个整数，表示山峰和山谷的数量。

数据范围
$1 \leq n \leq 1000,$
$0≤w≤10^9$

输入样例1：

输出样例1：

2 1

输入样例2：

输出样例2：

3 3

同样是一道Flood Fill模型题，本题需要搜两种连通块的数量。

从题目中需要注意的点：

如果一个点周围既有低的点又有高的点，那这个点既不算山峰也不算山谷
如果一个点周围既没有高的点有没有低的点，那这个点既是山峰又是山谷

搜的时候需要注意的点：

在搜的时候如果扩展到了搜过的点不能直接跳，因为这个点需要用来判别当前点是山峰还是山谷。比如你已经搜过了中间的一个比当前点低部分然后你将其直接跳过，那么这个点就可能变为了没有更低的点的情况，产生错误。

代码：

#include<iostream>
#include<queue>
using namespace std;
const int N = 1010;
const int dx[8] = { 1,0,-1,0,1,1,-1,-1 };	//八连通
const int dy[8] = { 0,1,0,-1,1,-1,1,-1 };
#define pii pair<int,int>
#define x first
#define y second

int n;
int g[N][N];
bool st[N][N];
bool has_higher = 0;
bool has_lower = 0;

void bfs(int ix, int iy) {
	queue<pii>q;
	q.push({ ix,iy });
	st[ix][iy] = 1;

	while (q.size()) {
		auto t = q.front();
		q.pop();

		for (int i = 0; i < 8; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];

			//这里先不排除搜过的点，如果排除的话会导致没办法判清楚山峰山谷
			if (xx >= 1 && xx <= n && yy >= 1 && yy <= n) {	

				if (g[xx][yy] > g[t.x][t.y])has_higher = 1;		//有比当前点高的点
				else if (g[xx][yy] < g[t.x][t.y])has_lower = 1;	//有比当前点低的点
				else {						//如果是相等的，也就是连通起来的
					if (!st[xx][yy]) {		//如果没搜过就压入队列
						st[xx][yy] = 1;
						q.push({ xx,yy });
					}
				}
			}
		}
	}
}

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> g[i][j];
		}
	}


	int valley = 0;	//记录山谷
	int peak = 0;	//记录山峰
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (!st[i][j]) {
				bfs(i, j);

				//自动排除了又有高的又有低的点
				if (!has_lower)valley++;	//如果没有更低的点
				if (!has_higher)peak++;		//如果没有更高的点

				has_lower = 0;	//重置
				has_higher = 0;
			}
		}
	}

	cout << peak << " " << valley << endl;
	return 0;
}

最短路模型

例题

1.AcWing 1076. 迷宫问题

给定一个 $n \times n$ 的二维数组，如下所示：

int maze[5][5] = {

0, 1, 0, 0, 0,

0, 1, 0, 1, 0,

0, 0, 0, 0, 0,

0, 1, 1, 1, 0,

0, 0, 0, 1, 0,

};

它表示一个迷宫，其中的 $1$ 表示墙壁， $0$ 表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

数据保证至少存在一条从左上角走到右下角的路径。

输入格式
第一行包含整数 $n$ 。
接下来 $n$ 行，每行包含 $n$ 个整数 $0$ 或 $1$ ，表示迷宫。

输出格式
输出从左上角到右下角的最短路线，如果答案不唯一，输出任意一条路径均可。

按顺序，每行输出一个路径中经过的单元格的坐标，左上角坐标为 $(0, 0)$ ，右下角坐标为 $(n - 1, n - 1)$ 。

数据范围
$0 \leq n \leq 1000$
输入样例：

输出样例：

此题要求记录并输出最短路径，因为BFS自己第一次搜出来就一定是一个最短路径，所以直接使用数组记录路径就可以。

要不然就是倒着记录路径正着搜，然后倒着输出，要不然就是倒着搜正着输出。

并且题目要求输出坐标，所以要用pair来存路径。

代码：

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
#define pii pair<int,int>
#define x first
#define y second
const int N = 1010;
const int dx[4] = { 0,1,0,-1 };
const int dy[4] = { 1,0,-1,0 };

int n;
int g[N][N];    
pii next[N][N]; //pair存路径，因为要求输出坐标，同时兼顾判断搜没搜过某点的功能

void bfs(int ix, int iy) {
	queue<pii>q;
	q.push({ ix,iy });
	
	memset(next, -1, sizeof next);  //初始化为-1，用于之后判定是否搜过某点
	
	next[ix][iy] = { 0,0 }; //标记上起点

	while (q.size()) {
		auto t = q.front();
		q.pop();
		
		for (int i = 0; i < 4; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];
			                                             //只有0能走
			if (xx >= 0 && xx < n && yy >= 0 && yy < n && !g[xx][yy] && next[xx][yy].x == -1) {
				q.push({ xx,yy });
				next[xx][yy] = t;   //记录路径
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);

	cin >> n;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> g[i][j];
		}
	}

	bfs(n - 1, n - 1);  //倒着搜，从终点找起点，这样得到的路径记录是正着的

	pii end(0, 0);  //从0 0开始
	while (1) {
		cout << end.x << " " << end.y << endl;
		if (end.x == n - 1 && end.y == n - 1)break; //当输出完终点之后就break
		end = next[end.x][end.y];    //转移到下一个路径
	}

	return 0;
}

AcWing 188. 武士风度的牛

农民 John 有很多牛，他想交易其中一头被 Don 称为 The Knight 的牛。

这头牛有一个独一无二的超能力，在农场里像 Knight 一样地跳（就是我们熟悉的象棋中马的走法）。

虽然这头神奇的牛不能跳到树上和石头上，但是它可以在牧场上随意跳，我们把牧场用一个 $x ， y$ 的坐标图来表示。

这头神奇的牛像其它牛一样喜欢吃草，给你一张地图，上面标注了 The Knight 的开始位置，树、灌木、石头以及其它障碍的位置，除此之外还有一捆草。

现在你的任务是，确定 The Knight 要想吃到草，至少需要跳多少次。

The Knight 的位置用 K来标记，障碍的位置用 * 来标记，草的位置用 H来标记。

这里有一个地图的例子：

             11 | . . . . . . . . . .
             10 | . . . . * . . . . . 
              9 | . . . . . . . . . . 
              8 | . . . * . * . . . . 
              7 | . . . . . . . * . . 
              6 | . . * . . * . . . H 
              5 | * . . . . . . . . . 
              4 | . . . * . . . * . . 
              3 | . K . . . . . . . . 
              2 | . . . * . . . . . * 
              1 | . . * . . . . * . . 
              0 ----------------------
                                    1 
                0 1 2 3 4 5 6 7 8 9 0

The Knight 可以按照下图中的 $A, B, C, D$ … 这条路径用 $5$ 次跳到草的地方（有可能其它路线的长度也是 $5$ ）：

             11 | . . . . . . . . . .
             10 | . . . . * . . . . .
              9 | . . . . . . . . . .
              8 | . . . * . * . . . .
              7 | . . . . . . . * . .
              6 | . . * . . * . . . F<
              5 | * . B . . . . . . .
              4 | . . . * C . . * E .
              3 | .>A . . . . D . . .
              2 | . . . * . . . . . *
              1 | . . * . . . . * . .
              0 ----------------------
                                    1
                0 1 2 3 4 5 6 7 8 9 0

注意：数据保证一定有解。

输入格式
第 $1$ 行：两个数，表示农场的列数 $C$ 和行数 $R$ 。

第 $2.. R + 1$ 行: 每行一个由 $C$ 个字符组成的字符串，共同描绘出牧场地图。

输出格式
一个整数，表示跳跃的最小次数。

数据范围
$1 \leq R, C \leq 150$
输入样例：

10 11
..........
....*.....
..........
...*.*....
.......*..
..*..*...H
*.........
...*...*..
.K........
...*.....*
..*....*..

输出样例：

#include<iostream>
#include<cstring>
#include<queue>
#define x first
#define y second
#define pii pair<int,int>
using namespace std;
const int N = 160;
const int dx[8] = { 1,1,-1,-1,2,2,-2,-2 };  //走日字
const int dy[8] = { 2,-2,2,-2,1,-1,1,-1 };

int n, m;
char g[N][N];
int dis[N][N];  //记录距离并且标记是否走过

int bfs() {
	memset(dis, -1, sizeof dis);    //初始化

	int ix, iy;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			if (g[i][j] == 'K')ix = i, iy = j;  //找起点
		}
	}

	queue<pii>q;
	q.push({ ix,iy });
	dis[ix][iy] = 0;    //起点距离设为0

	while (q.size()) {
		auto t = q.front();
		if(g[t.x][t.y] == 'H')return dis[t.x][t.y];
		q.pop();

		for (int i = 0; i < 8; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];

			if (xx >= 0 && xx < n && yy >= 0 && yy < m && g[xx][yy] != '*' && dis[xx][yy] == -1) {
				dis[xx][yy] = dis[t.x][t.y] + 1;    //更新距离
				q.push({xx,yy});
			}
		}
	}
}

int main() {
	cin >> m >> n;  //先读入列再读入行
	for (int i = 0; i < n; i++) cin >> g[i];

	cout << bfs() << endl;
	return 0;
}

AcWing 1100. 抓住那头牛

农夫知道一头牛的位置，想要抓住它。

农夫和牛都位于数轴上，农夫起始位于点 $N$ ，牛位于点 $K$ 。

农夫有两种移动方式：

从 X 移动到 $X - 1$ 或 $X + 1$ ，每次移动花费一分钟
从 X 移动到 $2 * X$ ，每次移动花费一分钟假设牛没有意识到农夫的行动，站在原地不动。

农夫最少要花多少时间才能抓住牛？

输入格式
共一行，包含两个整数 $N$ 和 $K$ 。

输出格式
输出一个整数，表示抓到牛所花费的最少时间。

数据范围
$0≤N,K≤10^5$

输入样例：

5 17

输出样例：

利用BFS的最短路的特性，直接搜遍所有情况，最终一定能够得到一个最短距离。

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1e5 + 10;

int n, k;
int q[N];
int dis[N];

int bfs() {
	memset(dis, -1, sizeof dis);

	dis[n] = 0;
	queue<int>q;
	q.push(n);

	while (q.size()) {
		int t = q.front();
		q.pop();

		if (t == k)return dis[t];		//找到终点了，返回距离

		if (t + 1 < N && dis[t + 1] == -1) {	//如果还可以前进一步
			dis[t + 1] = dis[t] + 1;
			q.push({ t + 1 });
		}
		if (t - 1 >= 0 && dis[t - 1] == -1) {	//如果还可以后退一步
			dis[t - 1] = dis[t] + 1;
			q.push({ t - 1 });
		}
		if (t * 2 < N && dis[t * 2] == -1) {	//如果可以乘2
			dis[t * 2] = dis[t] + 1;
			q.push({ t * 2 });
		}
	}
}

int main() {
	cin >> n >> k;

	cout << bfs();

	return 0;
}

多源最短路

AcWing.173.矩阵距离

给定一个 $N$ 行 $M$ 列的 01 矩阵 $A ， A [i] [j]$ 与 $A [k] [l]$ 之间的曼哈顿距离定义为：

$d i s t (A [i] [j], A [k] [l]) = ∣ i - k ∣ + ∣ j - l ∣$
输出一个 $N$ 行 $M$ 列的整数矩阵 $B$ ，其中：

$B [i] [j] = min 1 \leq x \leq N, 1 \leq y \leq M, A [x] [y] = 1 d i s t (A [i] [j], A [x] [y])$
输入格式
第一行两个整数 $N, M$ 。

接下来一个 $N$ 行 $M$ 列的 01 矩阵，数字之间没有空格。

输出格式
一个 $N$ 行 $M$ 列的矩阵 $B$ ，相邻两个整数之间用一个空格隔开。

数据范围
$1 \leq N, M \leq 1000$

输入样例：

输出样例：

3 2 1 0
2 1 0 0
1 0 0 1

本题的意思就是求多个起点到达离其最近的1的距离。

可以设置一个虚拟的起点，然后让虚拟起点和所有的起点的边权为 $0$ ，之后进行BFS。
在本题中，我们要求的是所有点到达 $1$ 的最小距离，那么我们就可以直接把所有的 $1$ 点的距离设为 $0$ ，然后存入队列中，再用BFS来求出所有距离 $1$ 点最近的 $0$ 点的距离。

代码：

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1010;
#define pii pair<int,int>
#define x first
#define y second
const int dx[4] = {1,0,-1,0};
const int dy[4] = {0,1,0,-1};
int dis[N][N];
char g[N][N];
int n,m;

void bfs(){
    memset(dis,-1,sizeof dis);
    
    queue<pii>q;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            if(g[i][j] == '1'){
                dis[i][j] = 0;
                q.push({i,j});
            }
    
    while(q.size()){
        auto t = q.front();
        q.pop();
        
        for(int i = 0;i < 4;i++){
            int xx = t.x + dx[i],yy = t.y + dy[i];
            if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&dis[xx][yy] == -1){
                dis[xx][yy] = dis[t.x][t.y] + 1;
                q.push({xx,yy});
            }
        }
    }
}


int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            cin >> a[i][j];
            
    bfs();
    
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= m;j++)
            cout << dis[i][j] << " ";
            
        puts("");    
    }
    return 0;
}

最小路数模型

对于最小步数模型，常用的方法就是用哈希存状态，而不用原本的矩阵，并且基本的操作也映射到哈希存的状态上。

Acwing.1107.魔板

Rubik 先生在发明了风靡全球的魔方之后，又发明了它的二维版本——魔板。

这是一张有 8 个大小相同的格子的魔板：

1 2 3 4
8 7 6 5

我们知道魔板的每一个方格都有一种颜色。

这 8 种颜色用前 8 个正整数来表示。

可以用颜色的序列来表示一种魔板状态，规定从魔板的左上角开始，沿顺时针方向依次取出整数，构成一个颜色序列。

对于上图的魔板状态，我们用序列 (1,2,3,4,5,6,7,8) 来表示，这是基本状态。

这里提供三种基本操作，分别用大写字母 A，B，C 来表示（可以通过这些操作改变魔板的状态）：

A：交换上下两行；
B：将最右边的一列插入到最左边；
C：魔板中央对的4个数作顺时针旋转。

下面是对基本状态进行操作的示范：

A：

8 7 6 5
1 2 3 4

B：

4 1 2 3
5 8 7 6

C：

1 7 2 4
8 6 3 5

对于每种可能的状态，这三种基本操作都可以使用。

你要编程计算用最少的基本操作完成基本状态到特殊状态的转换，输出基本操作序列。

注意：数据保证一定有解。

输入格式
输入仅一行，包括 8 个整数，用空格分开，表示目标状态。

输出格式
输出文件的第一行包括一个整数，表示最短操作序列的长度。

如果操作序列的长度大于0，则在第二行输出字典序最小的操作序列。

数据范围
输入数据中的所有数字均为 1 到 8 之间的整数。

输入样例：

2 6 8 4 5 7 3 1

输出样例：

7
BCABCCB

对于本题的矩阵，直接哈希成排列的数字12345678，并且从这个纬度上考虑问题。

如果执行A操作，就会使其变为87654321
如果执行B操作，就会使其变为41236785
如果执行C操作，就会使其变为17245368

只需要确定哪个状态是由哪个状态转移过来的，记录下来之后只需要从终点倒推到起点就行了。

对于字典序，只需要保证是按照 ABC的顺序进行执行的，而只要按照A，B，C的执行顺序去扫，就能够保证字典序。
因为BFS的时候在前一个状态搜完搜到 $B$ 之后，之后的状态就不可能再搜到C，因为之前搜到 $B$ 的时候就已经标注好这个状态了。

代码：

#include<iostream>
#include<queue>
#include<unordered_map>
#include<algorithm>
using namespace std;

char g[2][4];
unordered_map<string,int>dis;
unordered_map<string,pair<char,string>>pre;
queue<string>q;

void changeTog(string st){	//将矩阵更新成字符串的模样
	for(int i = 0;i < 4;i++)g[0][i] = st[i];
	for(int i = 3,j = 4;i >= 0;i--,j++)g[1][i] = st[j];
}

string changeToString(){	//将矩阵对应的字符串转化出来
	string res;
	for(int i = 0;i < 4;i++)res += g[0][i];
	for(int i = 3;i >= 0;i--)res += g[1][i];

	return res;
}

//3个操作
string A(string st){	
	changeTog(st);		//每次先更新矩阵
	for(int i = 0;i < 4;i++)swap(g[0][i],g[1][i]);//直接交换上下两行
	return changeToString();
}

string B(string st){
	changeTog(st);
	char c1 = g[0][3],c2 = g[1][3];

	for(int i = 3;i > 0;i--){	
	    g[0][i] = g[0][i-1];	
		g[1][i] = g[1][i-1];
	}

	g[0][0] = c1;
	g[1][0] = c2;
	return changeToString();
}

string C(string st){
	changeTog(st);

	//转圈
	char c = g[0][1];
	g[0][1] = g[1][1];
	g[1][1] = g[1][2];
	g[1][2] = g[0][2];
	g[0][2] = c;

	return changeToString();
}

void bfs(string start,string end){
	q.push(start);
	dis[start] = 0;

	while(q.size()){
		auto t = q.front();
		q.pop();

		if(t == end)return;	//搜到终点状态了就返回

		string next[3];		//提取出三种操作得来的状态
		next[0] = A(t);
		next[1] = B(t);
		next[2] = C(t);

		//按ABC顺序搜三种状态
		for(int i = 0;i < 3;i++){
			if(dis.count(next[i]) == 0){
			    
				dis[next[i]] = dis[t] + 1;
				pre[next[i]] = {char(i + 'A'),t};
				
				if(next[i] == end)break;
				
				q.push(next[i]);
			}
		}
	}
}

int main(){
	int x;string start,end;
	
	for(int i = 0;i < 8;i++){
		cin >> x;
		end += (x + '0');
	}
	start = "12345678";

	bfs(start,end);

	cout << dis[end] << endl;

	string res;
	while(end != start){
		res += pre[end].first;
		end = pre[end].second;
	}

	reverse(res.begin(),res.end());

	//如果步数不为0才输出
	if(res.size())cout << res << endl;

	return 0;
}

双端队列广搜

AcWing.175.电路维修

达达是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女翰翰，从而被收留在地球上。

翰翰的家里有一辆飞行车。

有一天飞行车的电路板突然出现了故障，导致无法启动。

电路板的整体结构是一个 R 行 C 列的网格 $（ R, C \leq 500 ）$ ，如下图所示。

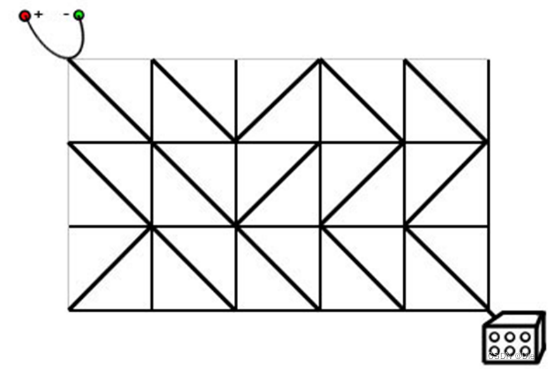
每个格点都是电线的接点，每个格子都包含一个电子元件。

电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。

在旋转之后，它就可以连接另一条对角线的两个接点。

电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

达达发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。

她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。

不过，电路的规模实在是太大了，达达并不擅长编程，希望你能够帮她解决这个问题。

注意：只能走斜向的线段，水平和竖直线段不能走。

输入格式
输入文件包含多组测试数据。

第一行包含一个整数 T，表示测试数据的数目。

对于每组测试数据，第一行包含正整数 R 和 C，表示电路板的行数和列数。

之后 R 行，每行 C 个字符，字符是"/“和”"中的一个，表示标准件的方向。

输出格式
对于每组测试数据，在单独的一行输出一个正整数，表示所需的最小旋转次数。

如果无论怎样都不能使得电源和发动机之间连通，输出NO SOLUTION。

数据范围
$1 \leq R, C \leq 500,$
$1 \leq T \leq 5$

输入样例：

1
3 5
\\/\\
\\///
/\\\\

输出样例：

样例解释
样例的输入对应于题目描述中的情况。

只需要按照下面的方式旋转标准件，就可以使得电源和发动机之间连通。

对于这道题，就相当于有线连着的路径的边权是0，没有连起来的需要转一下电线才能走过去，所以边权是1。
那么就相当于在这个边权为0或1的图上搜最短路的问题。

在这里使用双端队列，如果搜到了边权为0的点，就压入队头，如果搜到了边权为1的点，就压入队尾。在这种条件下，可以始终维护队列的两段性和单调性。

并且应注意，如果当前点的横纵坐标的和是偶数，那么就一定到不了横纵坐标之和为奇数的点，反之同理。

CODE:

#include <iostream>
using namespace std;
#define pii pair<int, int>
const int N = 510, M = N * N;
const int dx[4] = {-1,-1,1,1};
const int dy[4] = {-1,1,1,-1};

int n, m;
char g[N][N];
int dis[N][N];
bool st[N][N];

int bfs(){
    memset(st,0,sizeof st);
    memset(dis,0x3f,sizeof dis);

    deque<pii>q;
    q.push_back({0,0});
    dis[0][0] = 0;    

    char c[5] = "\\/\\/";//这里存的是应该是什么样的方向才是正确的

    int ix[4] = {-1,-1,0,0},iy[4] = {-1,0,0,-1};//扩展图的下标

    while(q.size()){
        auto t = f.front();
        q.pop_front();

        int x = t.first,y = t.second;
        if(x == n && y == m)return dis[x][y];

        if(st[x][y])continue;
        st[x][y] = 1;

        for(int i = 0;i < 4;i++){
            int a = x + dx[i],b = y + dy[i];

            if(a >= 0 && a <= n && b >= 0 && b <= m){
                int ga = x + ix[i],gb = y + iy[i];

                int w = (g[ga][gb] != c[i]);

                if(g[ga][gb] + w <= dis[a][b]){
                    dis[a][b] = d;

                    if(!w)q.push_front({a,b});  //如果是正确的字符，即边权为0，那么压入队头
                    else q.push_back({a,b});    //否则压入队尾
                }
            }
        }
    }
    return -1;
}

int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        cin >> n >> m;
        for (int i = 0; i < n; i++)
                cin >> g[i];

        if (n + m & 1) puts("NO SOLuTION\n");
        else cout << bfs() << endl;
    }
    return 0;
}