目录
一、 优先级队列的介绍
二、优先级队列的使用
2.1 建大堆 less
2.2 建小堆 greater
2.3 详解 greater 与 less
三、 priority_queue 的模拟实现
3.1 编写框架
3.2 编写简单函数
3.2 进堆 向上调整
3.3 出堆 向下调整
四、完整代码
一、 优先级队列的介绍
1. 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。
2. 其内容类似于堆,在堆中可以随时插入元素,并且只能检索最大堆元素(优先队列中位于顶部的元素)。
3. 优先队列被实现为容器适配器,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的成员函数来访问其元素。元素从特定容器的“尾部”弹出,其称为优先队列的顶部。
4. 底层容器可以是任何标准容器类模板,也可以是其他特定设计的容器类。容器应该可以通过随机访问迭代器访问,并支持以下操作:
empty():检测容器是否为空
size():返回容器中有效元素个数
front():返回容器中第一个元素的引用
push_back():在容器尾部插入元素
5. 标准容器类vector和deque满足这些需求。默认情况下,如果没有为特定的priority_queue类实例化指定容器类,则使用vector。
6. 需要支持随机访问迭代器,以便始终在内部保持堆结构。容器适配器通过在需要时自动调用算法函数 make_heap、push_heap 和 pop_heap 来自动完成此操作。
二、优先级队列的使用
优先级队列的传入参数有三个,分别是对象类型 T ,默认构造容器 Container , 比较方式 Compare ,从下图可以看出,后两个参数都有缺省值,当要改变堆中的比较方式时,要记得传入第二个模板参数!
2.1 建大堆 less
首先,优先级队列的首元素默认是最大的,如下图是默认情况下的对顶元素是堆中的最大值,库中默认缺省值为 less 。

2.2 建小堆 greater
但是,类似于 qsort 函数,可以提供特定的方式以达到特定的需求,如下,库中提供的 greater 可以使堆顶元素变为最小值:
除了上面实例化对象时的构造方式,可以在实例化对象时就传入参数:
vector<int> v = { 2, 9, 1, 6, 7, 4, 0 };
priority_queue<int, vector<int>, greater<int>> pq2(v.begin(), v.end());2.3 详解 greater 与 less
在C++中,std::greater 和 std::less 实际上是函数对象(也称为仿函数或者functors),而非简单的函数。一个函数对象是任何提供了函数调用运算符(operator())的对象。
这意味着,对象行为类似于函数:可以通过提供参数列表并使用圆括号语法来"调用"它。
下面直接来看一下 greater 与 less 的底层实现:
template<class T>
struct greater
{
bool operator()(T& left, T& right)
{
return left > right;
}
};
template<class T>
struct less
{
bool operator()(T& left, T& right)
{
return left < right;
}
};这样对于实例化对象时传入的 greater 或 less 就有了比较清晰的认识,而这也是不需要传入参数的原因,它们压根就不是个函数,而只是个对 () 的操作符重载。
这里先提一下下面的向上调整:

可以看到这里类似使用函数调用,但其实是创建了匿名类。
三、 priority_queue 的模拟实现
3.1 编写框架
如下,首先搭建一个框架:
template<class T>
struct greater
{
bool operator()(T& left, T& right)
{
return left > right;
}
};
template<class T>
struct less
{
bool operator()(T& left, T& right)
{
return left < right;
}
};
template <class T, class Container = std::vector<T>, class Compare = less<T> >
class my_priority_queue
{
public:
my_priority_queue()
{
_con();
}
void push(T x)
{}
void pop()
{}
size_t size()
{}
bool empty()
{}
// 堆顶元素不允许修改,因为:堆顶元素修改可以会破坏堆的特性
const T& top() const
{}
private:
Container _con;
};3.2 编写简单函数
从对 priority_queue 的介绍得知,有几个函数都是很好写的:
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
// 堆顶元素不允许修改,因为:堆顶元素修改可以会破坏堆的特性
const T& top() const
{
return _con.front();
}3.2 进堆 向上调整
但是, push 和 pop 会更复杂一些,这涉及到对堆内容的调整,调整的方法和 C语言 中堆的向上与向下调整算法大致相同,下面以 less 建大堆举例:

void AdjustUp(int child)
{
int father = (child - 1) / 2;
while (child > 0)
{
if (Compare()(_con[father], _con[child]))
{
swap(_con[child], _con[father]);
child = father;
father = (child - 1) / 2;
}
else
return;
}
}
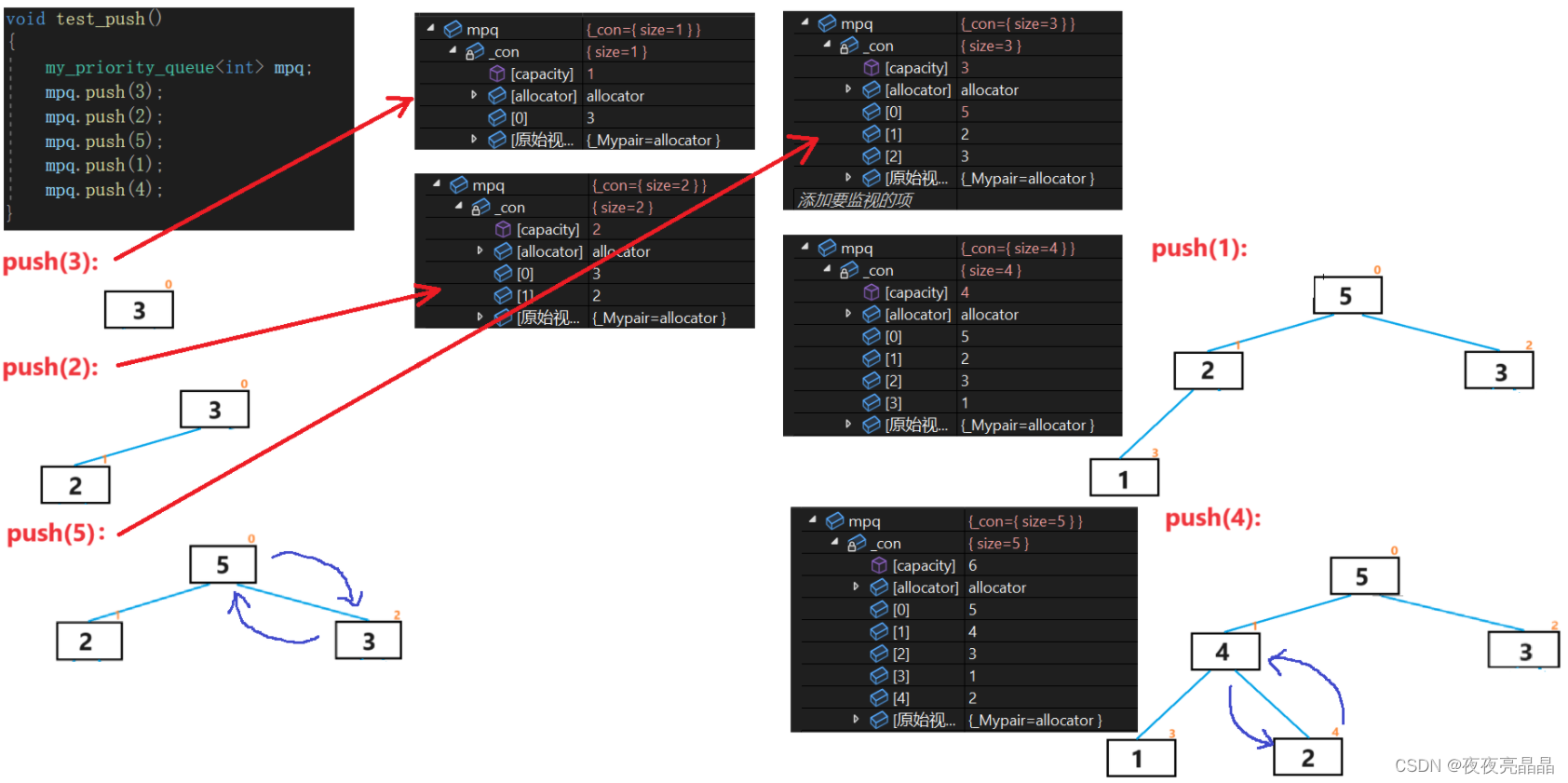
void push(T x)
{
_con.push_back(x);
AdjustUp(_con.size() - 1);
}暂时先组略的用调试的方法对照的看一下:
3.3 出堆 向下调整
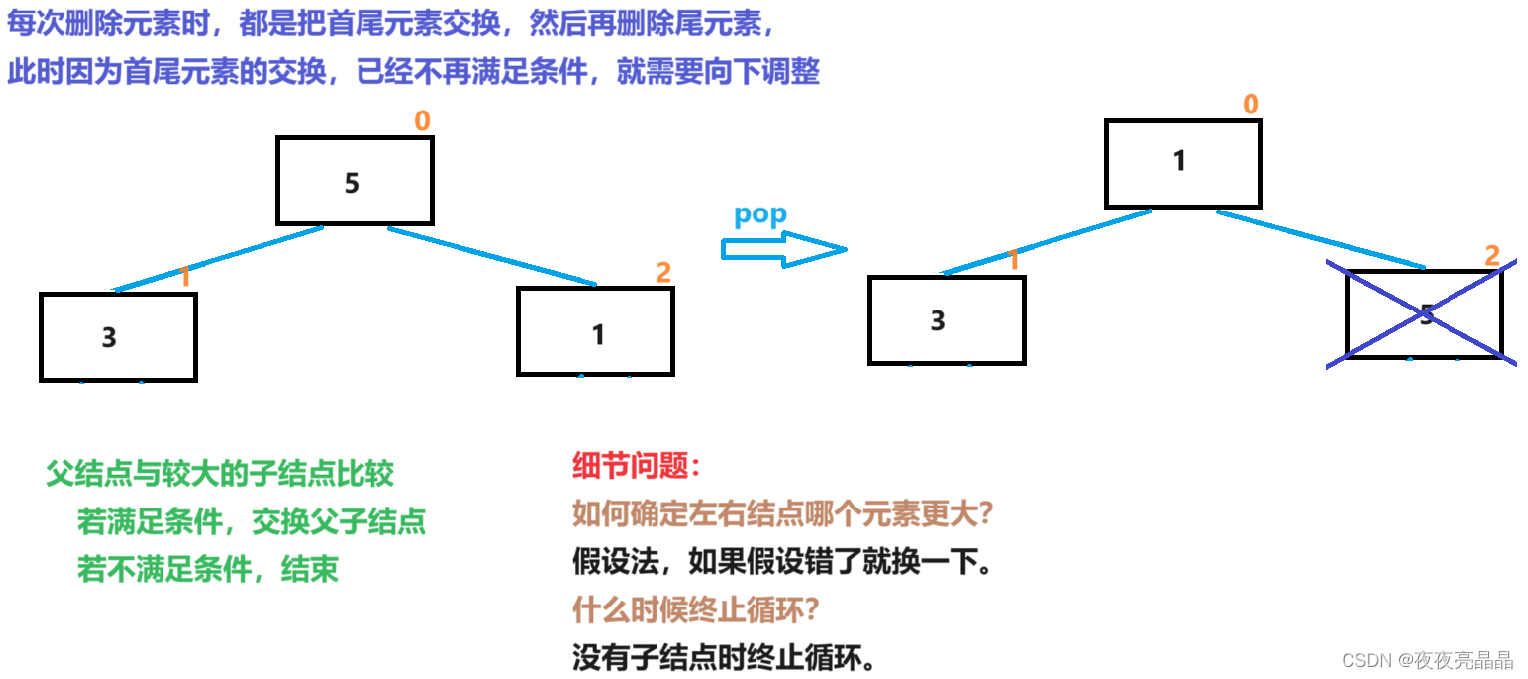
void AdjustDown()
{
int father = 0;
int child = father * 2 + 1;
while(child < _con.size())
{
if (child + 1 < _con.size() && Compare()(_con[child], _con[child + 1]))
child += 1;
if (_con[father] < _con[child])
{
swap(_con[father], _con[child]);
father = child;
child = father * 2 + 1;
}
else
return;
}
}
void pop()
{
if (_con.empty()) return;
swap(_con.front(), _con.back());
_con.pop_back();
AdjustDown();
}四、完整代码
#include <iostream>
#include<vector>
using namespace std;
namespace Flash
{
template<class T>
struct greater
{
bool operator()(T& left, T& right)
{
return left > right;
}
};
template<class T>
struct less
{
bool operator()(T& left, T& right)
{
return left < right;
}
};
template <class T, class Container = std::vector<T>, class Compare = less<T> >
class my_priority_queue
{
public:
my_priority_queue() : _con()
{}
void push(T x)
{
_con.push_back(x);
AdjustUp(_con.size() - 1);
}
void pop()
{
if (_con.empty()) return;
swap(_con.front(), _con.back());
_con.pop_back();
AdjustDown();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
// 堆顶元素不允许修改,因为:堆顶元素修改可以会破坏堆的特性
const T& top() const
{
return _con.front();
}
private:
void AdjustUp(int child)
{
int father = (child - 1) / 2;
while (child > 0)
{
if (Compare()(_con[father], _con[child]))
{
swap(_con[child], _con[father]);
child = father;
father = (child - 1) / 2;
}
else
return;
}
}
void AdjustDown()
{
int father = 0;
int child = father * 2 + 1;
while(child < _con.size())
{
if (child + 1 < _con.size() && Compare()(_con[child], _con[child + 1])) child += 1;
if (_con[father] < _con[child])
{
swap(_con[father], _con[child]);
father = child;
child = father * 2 + 1;
}
else
return;
}
}
private:
Container _con;
};
void test_push()
{
my_priority_queue<int> mpq;
mpq.push(3);
mpq.push(2);
mpq.push(5);
mpq.push(1);
mpq.push(4);
}
void test_pop()
{
my_priority_queue<int> mpq;
mpq.push(3);
mpq.push(2);
mpq.push(5);
mpq.push(1);
mpq.push(4);
while (!mpq.empty())
{
cout << mpq.top() << endl;
mpq.pop();
}
}
}