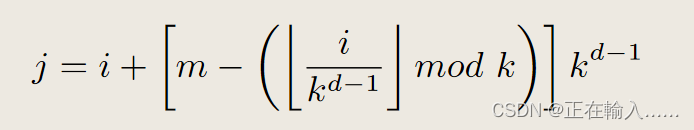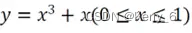图搜索算法是一个非常重要的概念，它是计算机科学中图论和算法设计的基础部分。在开始讨论图搜索算法之前，我们需要先理解什么是图以及图的基本结构。

什么是图？

图（Graph）是一种非线性数据结构，它由一组点（Nodes）和一组边（Edges）组成。点可以代表任何事物，比如网页、人、城市等等。边则代表点之间的联系，比如网页之间的链接、人与人之间的关系等等。

图有两种主要的类型：有向图（Directed Graph）和无向图（Undirected Graph）。在有向图中，边有方向，即边连接的两个点之间有一个方向。在无向图中，边没有方向，即边连接的两个点之间没有方向。

图的表示方法

图可以被表示为邻接矩阵（Adjacency Matrix）或邻接表（Adjacency List）。在邻接矩阵中，图被表示为一个矩阵，其中矩阵的每个元素表示两个点之间是否存在边。在邻接表中，图被表示为一个数组，其中每个元素都是一个链表，链表中的元素表示与该点相连的点。

图搜索算法

图搜索算法是用于查找图中从一个点到另一个点的路径的算法。它们可以用于解决许多问题，例如寻找最短路径、寻找最大生成树、寻找最小生成树等等。

图搜索算法的基本思想是从起点开始，沿着边遍历到终点，直到找到所需的路径。图搜索算法通常分为两种：广度优先搜索（BFS）和深度优先搜索（DFS）。

广度优先搜索（BFS）

广度优先搜索是一种图搜索算法，它从起点开始，沿着边遍历邻接点，直到找到终点。广度优先搜索的主要特点是它会优先搜索距离起点最近的点，然后再搜索距离起点稍远的点。

广度优先搜索的实现通常使用队列来存储待搜索的点。起点被放入队列中，然后从队列中取出第一个点，搜索它的邻接点，如果邻接点没有被访问过，则将其放入队列中。这个过程继续进行，直到队列为空或找到终点。

深度优先搜索（DFS）

深度优先搜索是一种图搜索算法，它从起点开始，沿着边遍历邻接点，直到找到终点。深度优先搜索的主要特点是它会优先搜索距离起点最远的点，然后再搜索距离起点稍近的点。

深度优先搜索的实现通常使用堆栈来存储待搜索的点。起点被放入堆栈中，然后从堆栈中取出第一个点，搜索它的邻接点，如果邻接点没有被访问过，则将其放入堆栈中。这个过程继续进行，直到堆栈为空或找到终点。

广度优先搜索和深度优先搜索的区别

广度优先搜索和深度优先搜索的主要区别在于它们的搜索顺序。广度优先搜索优先搜索距离起点最近的点，而深度优先搜索优先搜索距离起点最远的点。

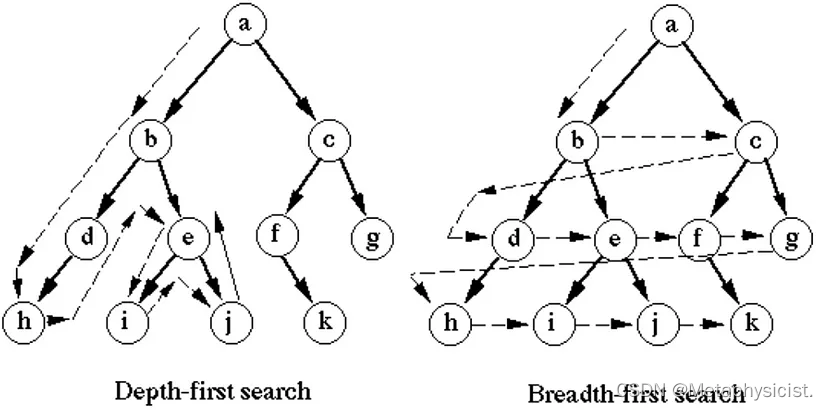
图搜索算法伪代码

广度优先搜索 (BFS)

def bfs(graph, start_node):
  # 初始化
  visited = set()
  queue = [start_node]
  
  while queue:
    # 取出队列中的第一个节点
    node = queue.pop(0)
    
    # 如果节点未被访问过
    if node not in visited:
      # 标记节点为已访问
      visited.add(node)
      
      # 处理节点 (例如，打印节点或进行其他操作)
      process(node)
      
      # 将节点的邻居节点加入队列
      for neighbor in graph[node]:
        if neighbor not in visited:
          queue.append(neighbor)

解释:

1. visited 集合用于记录已经访问过的节点。
2. queue 队列用于存储待访问的节点。
3. 循环遍历队列，直到队列为空。
4. 取出队列中的第一个节点，并检查是否已经访问过。
5. 如果未访问过，则标记为已访问，并进行处理。
6. 将该节点的所有邻居节点加入队列 (如果邻居节点未被访问过)。

深度优先搜索 (DFS)

def dfs(graph, start_node):
  # 初始化
  visited = set()
  
  def dfs_recursive(node):
    # 如果节点未被访问过
    if node not in visited:
      # 标记节点为已访问
      visited.add(node)
      
      # 处理节点 (例如，打印节点或进行其他操作)
      process(node)
      
      # 递归访问节点的邻居节点
      for neighbor in graph[node]:
        dfs_recursive(neighbor)
  
  # 从起点开始递归调用 DFS
  dfs_recursive(start_node)

解释:

1. visited 集合用于记录已经访问过的节点。
2. dfs_recursive 函数进行递归调用，实现DFS。
3. 检查节点是否已经访问过。
4. 如果未访问过，则标记为已访问，并进行处理。
5. 递归调用 dfs_recursive 函数，访问该节点的所有邻居节点。
6. 从起点开始调用 dfs_recursive 函数，启动DFS过程。

以上是BFS和DFS的伪代码示例，可以根据具体应用场景进行修改和扩展。

请注意，这些伪代码仅供参考，实际代码实现可能需要根据编程语言和数据结构进行调整。

图搜索算法的应用

图搜索算法在许多领域都有广泛的应用，例如：

1. 网络爬虫：网络爬虫使用图搜索算法来遍历网页，以便索引网页内容。

2. 路径规划：图搜索算法可以用于寻找从一个地点到另一个地点的最短路径，例如在地图应用中寻找从一个城市到另一个城市的最短路径。

3. 社交网络分析：图搜索算法可以用于分析社交网络中的关系，例如寻找两个人之间的最短路径或寻找社交网络中的社区。

4. 人工智能：图搜索算法可以用于解决许多人工智能问题，例如寻找最佳决策或寻找最优解。

总结

图搜索算法是计算机科学中图论和算法设计的基础部分。它们用于查找图中从一个点到另一个点的路径，并且在许多领域都有广泛的应用。广度优先搜索和深度优先搜索是两种主要的图搜索算法。广度优先搜索优先搜索距离起点最近的点，而深度优先搜索优先搜索距离起点最远的点。理解图搜索算法对于解决许多现实世界中的问题是非常重要的。无论是在网络爬虫、路径规划、社交网络分析还是人工智能领域，图搜索算法都发挥着关键作用。