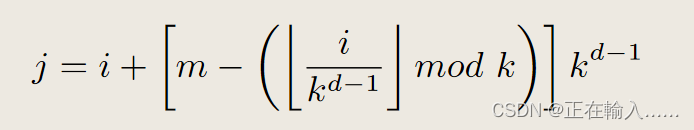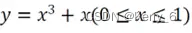A题太阳能路灯光伏板朝向问题

（完整版获取在文末）

 第1小问：计算每月15日的太阳直射强度和总能量

1. 理解太阳直射辐射和光伏板的关系**：光伏板接收太阳辐射并转化为电能，直射辐射对光伏板的效率影响最大。

2. 收集数据：使用附件中提供的2023年5月23日的太阳直射强度数据和1-12月份大气层外层太阳能辐射强度数值。

3. 计算太阳直射强度：根据光伏板的方位角和水平仰角，计算在不同倾角下光伏板受到的太阳直射强度。由于光伏板朝向正南方，主要考虑水平倾角对直射强度的影响。

4. 计算总能量：将每日的太阳直射强度乘以日照时间，累加得到每月的总能量。

 第2小问：设计光伏板的最佳固定朝向

1. 分析太阳直射辐射的季节性变化：根据附件中提供的1-12月份大气层外层太阳能辐射强度数值，分析太阳辐射的季节性变化规律。

2. 考虑地理位置：结合该城区的纬度和经度，考虑太阳在一年中的运动轨迹。

3. 模拟不同朝向下的接收能量：通过模拟或数学建模，计算不同朝向下光伏板一年中接收到的太阳直射辐射总能量。

4. 优化朝向：选择能使光伏板在一年中接收到最大平均太阳直射辐射总能量的朝向。

第3小问：设计最优朝向，考虑储电效率

1. 理解效率限制：光伏板在低强度和高强度直射辐射下转换效率都受限。

2. 定义理想直射强度范围：上午大于150 W/m²，下午大于100 W/m²。

3. 分析日辐射变化：使用附件中的日辐射数据，分析一天中太阳直射强度的变化。

4. 设计朝向：设计光伏板的朝向，使得在理想直射强度范围内的时间尽可能长。

5. 计算日均总能量和理想强度时长：通过计算，得出在设计的朝向下，光伏板晴天条件下的日均总能量和满足理想直射强度条件的时长。

实施步骤：

1. 数据处理：整理和分析附件中的数据，包括太阳直射强度和大气层外层太阳能辐射强度。

2. 数学建模：建立数学模型来模拟太阳直射强度和光伏板接收能量的关系。

3. 模拟分析：使用模拟软件或编程语言（如Python或MATLAB）来模拟不同朝向和倾角下的光伏板接收能量。

4. 优化算法：应用优化算法（如遗传算法、粒子群优化等）来寻找最佳朝向。

5. 结果验证：通过对比分析不同朝向下的模拟结果，验证所提出的最优朝向是否符合实际。

             B 题 使用行车轨迹估计交通信号灯周期问题

针对华中杯B题的四个小问，以下是每个小问的解决思路和可能用到的建模及机器学习算法：

### 第1小问：固定周期信号灯的估计

1. **数据分析**：首先分析附件1中的轨迹数据，确定车辆通过路口的模式。

2. **特征工程**：提取时间戳和车辆ID作为特征。

3. **周期性检测**：使用傅里叶变换（FFT）或自相关函数（ACF）来识别周期性。

4. **统计分析**：应用统计方法，如卡方检验，来确定车辆通过模式与信号灯周期的关系。

5. **模型建立**：使用简单的周期性回归模型，如正弦或余弦函数，来拟合信号灯周期。

### 第2小问：样本车辆比例和定位误差的影响

1. **模拟分析**：模拟不同样本车辆比例和定位误差对模型精度的影响。

2. **敏感性分析**：进行敏感性分析，了解不同因素如何影响周期估计的准确性。

3. **机器学习算法**：可能需要使用决策树或随机森林等算法来评估不同因素对模型输出的影响。

### 第3小问：变化信号灯周期的检测

1. **时间序列分析**：使用ARIMA或季节性分解的时间序列预测（STL）来识别周期性变化。

2. **异常检测**：采用异常检测算法，如Isolation Forest或One-Class SVM，来识别周期性变化的模式。

3. **实时监测**：设计一个实时监测系统，使用滑动窗口方法来持续分析信号灯周期。

### 第4小问：多方向信号灯周期的识别

1. **多变量分析**：分析所有方向的车辆轨迹数据，寻找共同的周期性模式。

2. **聚类算法**：使用K-means或DBSCAN等聚类算法来识别不同方向的周期性模式。

3. **深度学习**：可能需要使用深度学习算法，如LSTM或GRU，来处理复杂的时间序列数据。

### 通用步骤：

- **数据预处理**：包括数据清洗、缺失值处理、异常值检测和处理。

- **特征选择**：选择与信号灯周期最相关的特征进行分析。

- **模型选择**：根据问题的复杂性和数据的特点选择合适的模型。

- **模型训练与验证**：使用交叉验证等方法来训练和验证模型。

- **结果解释**：对模型的输出进行解释，确定信号灯周期及其变化。

           C题：基于光纤传感器的平面曲线重建算法建模

针对华中杯C题，我们可以根据题目要求，将问题分解为几个小问，并为每个小问提供解决思路。以下是每个小问的解决思路和可能用到的建模及机器学习算法：

### 问题1：估算传感点的曲率

1. **理解问题**：首先理解波长与曲率之间的关系，以及如何从波长变化估算曲率变化。

2. **数学建模**：使用给定的关系式 \( k = \frac{c(\lambda - \lambda_0)}{\lambda_0} \) 来计算每个传感器点的曲率，其中 \( c \) 是常数，\( \lambda_0 \) 是初始波长，\( \lambda \) 是受力后的波长。

3. **数据处理**：处理表1中的波长数据，计算每个传感器在两种状态下的曲率。

### 问题2：重构平面曲线

1. **曲线拟合**：使用问题1中计算出的曲率数据，通过多项式拟合或其他曲线拟合技术来重构曲线。

2. **参数选择**：确定初始点坐标、水平方向和垂直方向的定义，以及切线与水平方向的夹角。

3. **模型建立**：基于这些参数和曲率数据，构建一个数学模型来估算不同横坐标位置处的曲率。

### 问题3：重构平面曲线并分析误差

1. **采样点选择**：根据给定的平面曲线方程 \( y = f(x) \)，以适当的等间距弧长采样来确定曲线上的点。

2. **曲率计算**：对这些采样点使用问题1中的模型来计算曲率。

3. **误差分析**：比较重构曲线与原始曲线之间的差异，分析误差来源，如采样密度、模型假设等。

### 通用步骤：

- **数据预处理**：确保数据的准确性和完整性。

- **模型选择**：根据问题的具体情况选择适当的数学模型和算法。

- **算法实现**：使用适当的编程语言（如Python、MATLAB）来实现所选模型和算法。

- **结果验证**：通过比较模型预测与实际数据来验证模型的有效性。

对于C题，主要涉及的是数学建模和物理原理的应用，而不是传统意义上的机器学习问题。因此，可能用到的算法和技术包括：

- **多项式回归**：用于曲线拟合。

- **数值分析方法**：如牛顿法、梯度下降等，用于优化问题求解。

- **微积分**：用于计算曲率和其他导数相关的量。

- **计算机图形学**：用于可视化重构的曲线和分析误差。

2024华中杯A题完整思路+完整数据+可执行代码+后续参考论文


2024华中杯B题完整思路+完整数据+可执行代码+后续参考论文


2024华中杯C题完整思路+完整数据+可执行代码+后续参考论文