java1算法

news2024/11/17 15:56:39

排序–comparable接口

java提供了一个接口Comparable用来定义类的排序规则
eg:
1、定义一个学生类Student，具有年龄age和姓名username连个属性，并通过Comparable接口提供比较规则；
2、定义测试类Test,在测试类中定义测试方法Comparable getMax(Comparable c1,Comparable ca)完成测试

package com.arithmetic.sort;

import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;
import lombok.experimental.Accessors;

//1、定义一个学生类Student，具有年龄age和姓名username连个属性，并通过Comparable接口提供比较规则；
@Data
@AllArgsConstructor
@NoArgsConstructor
@Accessors(chain = true)
public class Student implements Comparable<Student>{

    private String username;
    private int age;

    @Override
    public int compareTo(Student o) {
        return this.age - o.age;
    }
}

package com.arithmetic.test;

import com.arithmetic.sort.Student;

//2、定义测试类Test,在测试类中定义测试方法Comparable getMax(Comparable c1,Comparable ca)完成测试
public class TestComparable {

    public static void main(String[] args) {
//        创建两个Student对象，并调用getMax方法
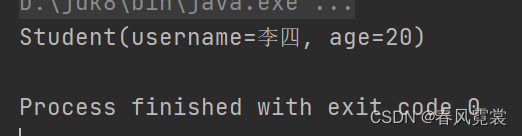
        Student s1 = new Student();
        s1.setUsername("张三");
        s1.setAge(18);

        Student s2 = new Student();
        s2.setUsername("李四");
        s2.setAge(20);

        Comparable max = getMax(s1, s2);
        System.out.println(max);


    }


    public static Comparable getMax(Comparable c1,Comparable c2){

        int result = c1.compareTo(c2);
//        如果result<0,则c1 比c2大
//        如果result>0,则c1 比c2小
//        如果result==0,则c1 比c2一样大
        if(result >= 0){
            return c1;
        }else {
            return c2;
        }

    }

}

在这里插入图片描述

简单排序—（1）冒泡排序

需求：
排序前：{4,5,6,3,2,1}
排序后：{1,2,3,4,5,6}

原理：
1、比较相邻的元素。如果前一个元素比后一个元素大，就交换这两个元素位置。
2、对每一对相邻元素做同样的工作，从开始第一对元素到结尾的最后一对元素。最终最后位置的元素就是最大值
在这里插入图片描述

package com.arithmetic.sort;

public class Bubble {

    /*
    * 对数组a中的元素进行排序
    * */
    public static void sort(Comparable[] a){

        for(int i = a.length -1; i > 0;i--){//外层循环决定纵冒泡次数
            for(int j=0;j< i;j++){//内层循环去交换数据，冒泡
//                比较索引j和索引j+1处的值
                if(greater(a[j],a[j+1])){
                    exch(a,j,j+1);
                }
            }
        }

    }

    /*
    * 比较v元素是否大于w元素
    * */
    private static boolean greater(Comparable v,Comparable w){
        return v.compareTo(w) > 0;
    }

    /*
    * 数组元素i和j交换位置
    * */
    private static void exch(Comparable[] a,int i,int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

}

package com.arithmetic.test;

import com.arithmetic.sort.Bubble;

import java.util.Arrays;

public class BubbleTest {

    public static void main(String[] args) {

        Integer[] arr = {4,5,6,3,2,1};

        Bubble.sort(arr);
        System.out.println(Arrays.toString(arr));

    }

}

总结：
外层循环决定纵冒泡次数，内层循环去交换数据，冒泡
时间复杂度分析：
冒泡排序使用了双层for循环，其中内层循环的循环体是真正完成排序的代码，所以，我们分析冒泡排序的时间复杂度，注意分析一下内层循环体的执行次数即可。
在最坏情况下，也就是加入要排序的元素为{6,5,4,3,2,1}逆序，那么：
元素比较的次数为：
(N-1)+(N-2)+(N-3)+…+2+1 = ((N-1)+1)(N-1)/2=N^2/2-N/2;
元素交换次数为：
(N-1)+(N-2)+(N-3)+…+2+1 = ((N-1)+1)(N-1)/2=N^2/2-N/2;
总执行次数为：
(N^2/2-N/2) + (N ^2/2-N/2) = N ^2-N;

安照大O推导法则，保留函数中的最高阶项，那么最终冒泡排序的时间复杂度为O(N^2).

简单排序—（2）选择排序

原理：
1、每一次遍历的过程中，都假定第一个索引处的元素是最小值，和其他索引处的值依次进行比较，如果当前索引处的值大于其他某个索引处的值，则假定其他某个索引处的值为最小值，最后可以找到最小值所在的索引
2、交换第一个索引处和最小值所在的索引处的值
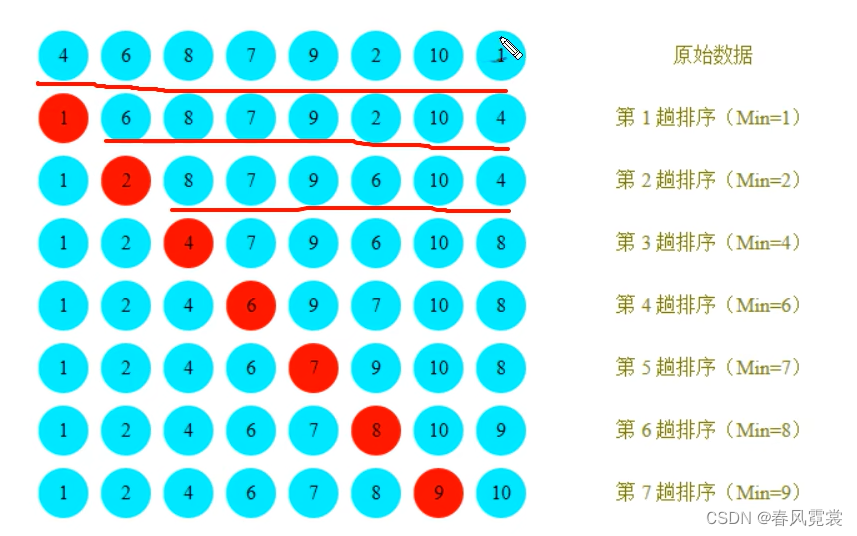
在这里插入图片描述
需求：
排序前：{4,6,8,7,9,2,10,1}
排序后：{1, 2, 4, 6, 7, 8, 9, 10}

package com.arithmetic.sort;

public class Selection {

    /*
     * 对数组a中的元素进行排序
     * */
    public static void sort(Comparable[] a){
        //选择排序是按照大小顺序来的，所以外层循环可以比总数小1，就是后的那个树是自然结果
       for(int i=0; i<=a.length -2;i++){
//       定义一个变量，记录最小元素所在的索引，默认为参与选择排序的第一个元素所在的位置
            int minIndex = i;
           for (int j = i+1; j < a.length; j++) {
//             需要比较最小索引minIndex处的值和j索引处的值;
               if(greater(a[minIndex],a[j])){
                    minIndex = j;
               }
           }
//          交换最小元素所在索引MinIndex处的值和索引i处的值
           exch(a,i,minIndex);

       }

    }

    /*
     * 比较v元素是否大于w元素
     * */
    private static boolean greater(Comparable v,Comparable w){
        return v.compareTo(w) > 0;
    }

    /*
     * 数组元素i和j交换位置
     * */
    private static void exch(Comparable[] a,int i,int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

}

package com.arithmetic.test;

import com.arithmetic.sort.Selection;

import java.util.Arrays;

public class SelectTest {

    public static void main(String[] args) {

        Integer[] arr = {4,6,8,7,9,2,10,1};
        Selection.sort(arr);
        System.out.println(Arrays.toString(arr));

    }

}

在这里插入图片描述
总结：
选择排序，就是根据该索引值得排序值，如0索引按从小到大，内存循环就要找到最小的值放在0索引处，和冒泡不同的是冒泡是相邻间相比，把大的往后面冒泡，而选择是找出最大或最小的值放在相应的索引处（按照顺序），不用每比较一下，相邻间就交换位置
时间复杂度分析：
选择排序使用了双层for循环，其中外层循环完成了数据交换，内层循环完成了数据比较，所以我们分别统计数据交换次数和数据比较次数；
数据比较次数：
(N-1)+(N-2)+(N-3)+…+2+1 = ((N-1)+1)*(N-1)/2=N^2/2-N/2;
数据交换次数：
N-1
时间复杂度：
N^2/2-N/2 + N-1 = N ^ 2/2 + N/2 -1；
安照大O推导法则，保留函数中的最高阶项，那么最终冒泡排序的时间复杂度为O(N^2).

简单排序—（3）插入排序

在这里插入图片描述
原理:
1、把所有的元素分为两组，已经排序的和未排序的；
2、找到未排序的组中的第一个元素，向已经排序的组中进行插入；
3、倒叙遍历已经排序的元素，依次和待插入的元素进行比较，直到找到一个元素小于等于待插入元素，那么就把待插入元素放到这个位置，其他的元素向后移动一位；

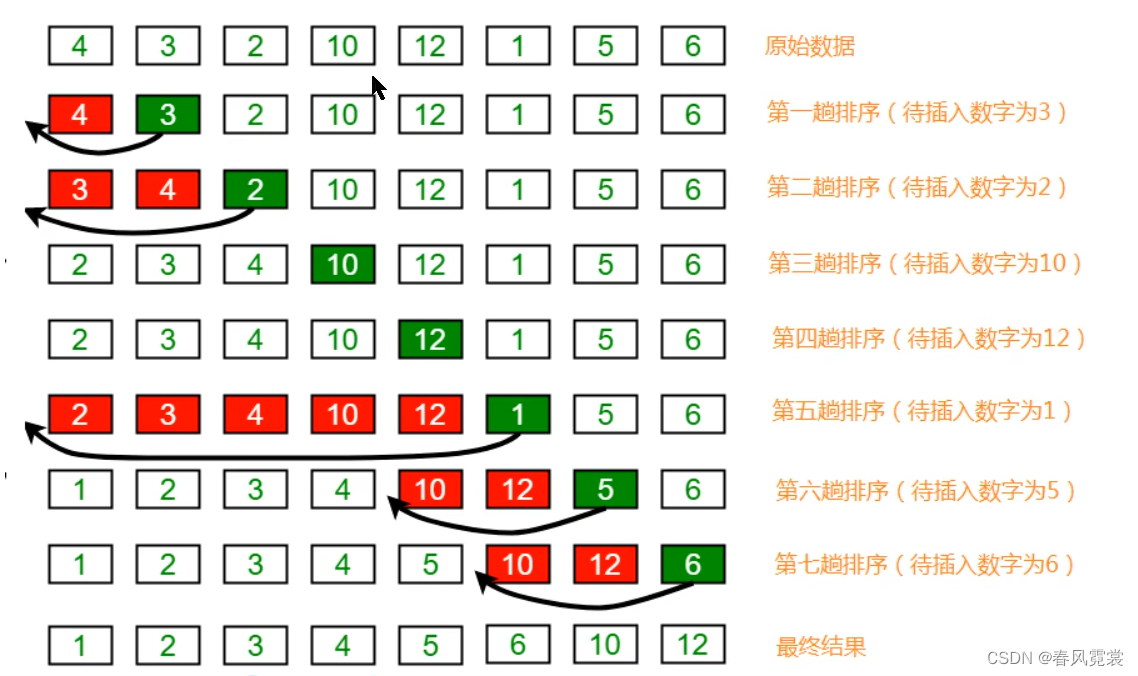
在这里插入图片描述
需求：
排序前：{4,3,2,10,12,1,5,6}
排序后：{1, 2, 3, 4, 5, 6, 10, 12}

package com.arithmetic.sort;

public class Insertion {

    /*
     * 对数组a中的元素进行排序
     * */
    public static void sort(Comparable[] a){

        for (int i = 1; i < a.length; i++) {
            for (int j = i; j > 0 ; j--) {
//                比较索引j处的值和索引j-1处的值，如果索引j-1处的值比索引j处的值大，则交换数据，
//                如果不大,那么就找到合适的位置了,退出循环即可;
                if(greater(a[j-1],a[j])){
                    exch(a,j-1,j);
                }else {
                    break;
                }

            }

        }

    }

    /*
     * 比较v元素是否大于w元素
     * */
    private static boolean greater(Comparable v,Comparable w){
        return v.compareTo(w) > 0;
    }

    /*
     * 数组元素i和j交换位置
     * */
    private static void exch(Comparable[] a,int i,int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

}

package com.arithmetic.test;

import com.arithmetic.sort.Bubble;
import com.arithmetic.sort.Insertion;

import java.util.Arrays;

public class InsertionTest {

    public static void main(String[] args) {
        Integer[] arr = {4,3,2,10,12,1,5,6};

        Insertion.sort(arr);
        System.out.println(Arrays.toString(arr));
    }

}

总结：
插入排序就和打牌放牌的操作类似，将第二个数和前面排好顺序的数比较，这里是从小到大，如果现在的比前面的小，就和前面的数换位置，直到比前面的数大，就退出内层循环（这里和冒泡相似，但是有退出循环条件）

时间复杂度：
插入排序使用了双层for循环，其中内层循环体是真正完成排序的代码，所以我们分析插入排序的时间复杂度，主要分析内层循环体执行次数即可。
最坏情况：
比较次数为：
(N-1)+(N-2)+(N-3)+…+2+1 = ((N-1)+1)(N-1)/2=N^2/2-N/2;
交换次数为：
(N-1)+(N-2)+(N-3)+…+2+1 = ((N-1)+1)(N-1)/2=N^2/2-N/2;
总执行次数为：
(N^2/2-N/2) + (N ^2/2-N/2) = N ^2-N;

安照大O推导法则，保留函数中的最高阶项，那么最终冒泡排序的时间复杂度为O(N^2).

复杂排序—（1）希尔排序

希尔排序是插入排序的一种，又称"缩小增量排序"，是插入排序算法的一种更高效的改进版本。
主要是通过分组降低时间复杂度
原理：
1、选定一个增长量h,按照增长量h作为数据分组的依据，对数据进行分组；
2、对分组的每一组数据完成插入排序；
3、减小增长量，最小减为1，重复第二步操作。

复杂排序—（2）归并排序

复杂排序—（3）快速排序

排序稳定性

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/160365.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

还不会用YakitBp?来，我教你

还不会用YakitBp?来，我教你

前言 &#x1f340;作者简介&#xff1a;被吉师散养、喜欢前端、学过后端、练过CTF、玩过DOS、不喜欢java的不知名学生。 &#x1f341;个人主页&#xff1a;被吉师散养的职业混子 &#x1f342;相应专栏&#xff1a;CTF专栏 Yakit介绍 好兄弟&#xff0c;你听说过yakit吗&…
阅读更多...
Redis五大基本数据类型

Redis五大基本数据类型

Redis五大基本数据类型 1.Redis通用命令 常用命令 #Redis的键key操作 keys * 表示查看当前库所有key 【注意是&#xff1a;可以使用通配符】 exists <key> 表示判断某个key是否存在&#xff0c;存在返回1&#xff0c;否则返回0 type <key> 表示判断key类型 del …
阅读更多...
fiddler的下载和安装，及常用操作

fiddler的下载和安装，及常用操作

目录 一、fiddler介绍 二、fiddler的下载和安装 三、fiddler的简单配置 四、fiddler的抓包 五、fiddler的自动响应器 六、fiddler的断点 七、fiddler的构造器 一、fiddler介绍 Fiddler是比较好用的Web代理调试工具之一&#xff0c;它能记录并检查所有客户端与服务端的HT…
阅读更多...
【SpringCloud09】Ribbon负载均衡服务调用

【SpringCloud09】Ribbon负载均衡服务调用

1.概述 1.1是什么 Spring Cloud Ribbon是基于Netflix Ribbon实现的一套客户端负载均衡的工具。 简单的说&#xff0c;Ribbon是Netflix发布的开源项目&#xff0c;主要功能是提供客户端的软件负载均衡算法和服务调用。Ribbon客户端组件提供一系列完善的配置项如连接超时&…
阅读更多...
Java 如何设计一款小游戏详细讲解(一)

Java 如何设计一款小游戏详细讲解(一)

目录 介绍 讲解 步骤一 步骤二 阶段(一)详细代码 介绍 注&#xff1a;这里是参考黑马程序员课程&#xff0c;其中图片也是直接拿的黑马程序员提供的图片 其中游戏的代码主要参考黑马程序员的课程&#xff0c;登录和注册主要由自己完成。 黑马素材放到这里自取 链接: https…
阅读更多...
【Esp32】Spi接口驱动SX1268模块

【Esp32】Spi接口驱动SX1268模块

【Esp32】Spi接口驱动SX1268模块1.硬件接线2. SX1268 模块的 SPI 时序分析3. 基于 ESP32 实现函数封装3.1 读寄存器3.2 写寄存器4. 实验结果日期&#xff1a; 2023-01-13 项目需要用乐鑫的 ESP32开发板驱动 Lora 模块&#xff0c;用的是 深圳SX1268ZTR4-GC的lora模块&#xff…
阅读更多...
通行密钥，向无休止的修改密码说再见~

通行密钥，向无休止的修改密码说再见~

在上一期里《对称加密面临的那些挑战》中&#xff0c;我们提过密码&#xff0c;和多数人理解的不同&#xff0c;日常生活中用于保护账号安全的所谓“密码”&#xff0c;更贴切的称呼应该是“口令”密码。密码学中的密码&#xff0c;和我们日常生活中登录各类信息化系统所使用的…
阅读更多...
Vue--》基于Vue的UI组件库，大家应该熟悉并会使用

Vue--》基于Vue的UI组件库，大家应该熟悉并会使用

目录 PC端UI组件库 Element UI IView UI 移动端UI组件库 Vant Cube UI Mint UI Nut UI UI组件库&#xff1a;它是设计系统的一部分&#xff0c;是在我们常规界面设计过程中可以直接用来制作交互图例和搭建页面的组件集合&#xff0c;它可以作为单个组件独立存在&#x…
阅读更多...
Linux下的FrameBuffer驱动框架

Linux下的FrameBuffer驱动框架

一、RGB LCD经典显示器件介绍&#xff1a;1、LCD屏幕的重要属性参数&#xff1a;① 分辨率&#xff1a;也就是屏幕上的像素点的个数&#xff1b;② 像素格式&#xff1a;即单个像素点RGB三种颜色的表达方式&#xff0c;包括RGB888、ARGB8888和RGB565等。③ LCD屏幕硬件接口&…
阅读更多...
全网最全的Linux中的内核级加强型火墙图文详解

全网最全的Linux中的内核级加强型火墙图文详解

目录 前言 一、Selinux的功能 二、Selinux的状态及管理 三、Selinux的安全上下文 四、SEBOOL 五、SEPORT 六、setrouble 前言 内核级加强型火墙主要是指系统中的selinux功能&#xff0c;该功能开启时&#xff0c;会对系统中的文件和程序产生影响&#xff0c;用户的…
阅读更多...
SkyEye：针对飞行模拟器的仿真解决方案

SkyEye：针对飞行模拟器的仿真解决方案

01.飞行模拟器简介 飞行模拟器是一种由人工打造&#xff0c;能够尽可能真实地还原飞机飞行及空中环境的模拟系统&#xff0c;一般用于飞行员培训、飞机设计等工作。飞行模拟器能够模拟如何控制飞机飞行、模拟飞机应用系统的反应&#xff0c;还可模拟一些可能会对飞机系统造成影…
阅读更多...
java图片压缩

java图片压缩

1背景 查看各种文章&#xff0c;发现thumbnailator的压缩率和压缩效果都不错&#xff0c;thumbnailator又是使用java实现的&#xff0c;所以直接扒源码&#xff0c;找到了里面实现压缩的关键代码&#xff0c;封装成一个压缩工具类&#xff0c;有需要的同学可以参考。thumbnail…
阅读更多...
Linux多线程Web服务器（C++实现）

Linux多线程Web服务器（C++实现）

本文实现的是基于Reactor模式epoll&#xff08;边缘触发&#xff09;非阻塞socket非阻塞IO线程池的Web服务器&#xff0c;可以处理GET、POST两种请求&#xff0c;完成展示主页、获取图片、获取视频、登录及注册共五种功能。原理图&#xff1a;上图为本文实现的服务器的原理图&a…
阅读更多...
国产GPU芯片迎来突破，算力全球第一，中文编程也有好消息

国产GPU芯片迎来突破，算力全球第一，中文编程也有好消息

苦&#xff0c;芯片久矣&#xff0c;终&#xff0c;迎来突破&#xff0c;实在振奋人心&#xff01;最近&#xff0c;国产GPU芯片传来了好消息&#xff0c;国产自研首款通用芯片&#xff0c;以每秒千万亿次的计算能力&#xff0c;创全球算力记录&#xff0c;芯片领域实现跨越式的…
阅读更多...
包体积优化 · 实战论 · 怎么做包体优化? 做好能晋升吗? 能涨多少钱?

包体积优化 · 实战论 · 怎么做包体优化? 做好能晋升吗? 能涨多少钱?

“ 【小木箱成长营】包体积优化系列文章&#xff1a; 包体积优化 方法论 揭开包体积优化神秘面纱 包体积优化 工具论 初识包体积优化 BaguTree 包体积优化录播视频课 ”一、引言 Hello&#xff0c;我是小木箱&#xff0c;欢迎来到小木箱成长营系列教程&#xff0c;今天将分…
阅读更多...
论文投稿指南——中文核心期刊推荐（农业工程）

论文投稿指南——中文核心期刊推荐（农业工程）

【前言】 &#x1f680; 想发论文怎么办&#xff1f;手把手教你论文如何投稿&#xff01;那么&#xff0c;首先要搞懂投稿目标——论文期刊 &#x1f384; 在期刊论文的分布中&#xff0c;存在一种普遍现象&#xff1a;即对于某一特定的学科或专业来说&#xff0c;少数期刊所含…
阅读更多...
实战10：基于opencv的数字图像处理：边缘检测 （完整代码+详细教程）

实战10：基于opencv的数字图像处理：边缘检测 （完整代码+详细教程）

给出“离散拉普拉斯算子”一般形式的数学推导 离散值的导数使用差分代替： 所以： 以(x, y)为中心点，在水平和垂直方向上应用拉普拉斯算子，滤波器(对应a=1的情况)为：
阅读更多...
Spring Cloud Alibaba学习指南

Spring Cloud Alibaba学习指南

文章目录背景介绍主要功能主要组件参考文档Spring Cloud Alibaba githubNacos官方文档Nacos运维手册Sentinel官方文档Spring Cloud Alibaba SentinelSeata官方文档Spring Cloud Alibaba 英语文档应用脚手架背景 由于在2018年Netflix公司宣布对其核心组件Hystrix、Ribbon、zuul…
阅读更多...
远端连接服务器详解

远端连接服务器详解

昨天决定入手了一台腾讯轻量应用服务器&#xff0c;在连接的过程中遇到很多问题&#xff0c;浪费了很多时间&#xff0c;所以在这里对这些问题进行整理分享给大家&#xff01;&#xff01;&#xff01;系统的安装OpenCloudOS是完全中立、全面开放、安全稳定、高性能的操作系统及…
阅读更多...
JVM调优之GC日志分析及可视化工具介绍

JVM调优之GC日志分析及可视化工具介绍

JVM调优之GC日志分析及可视化工具介绍 文章目录JVM调优之GC日志分析及可视化工具介绍GC日志参数GC日志参数常用垃圾收集器参数GC日志分析日志的含义使用 ParNew Serial Old 的组合进行内存回收使用 Parallel Scavenge Parallel Old 的组合进行内存回收大对象回收分析日志分析…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023