向量组及其线性组合

一.向量、向量组

1.向量

n个有次序的数a1,a2,...,an所组成的数组称为n维向量，这n个数称为该向量的n个分量，第i个数ai称为第

i个分量

n维向量可以写成一行，也可以写成一列，在没有指明是行向量还是列向量时，均为列向量

2.向量组

若干个同维数的列向量（行向量）所组成的集合叫作向量组

含有限个向量的向量组可以构成一个矩阵

二.向量的线性组合和线性表示

1.线性组合

给定向量组A：a1,a2,...,am，对于任何一组实数k1,k2,...,km，表达式k1a1+k2a2+...+kmam称为向量组A的一个线性组合，k1,k2,...,km称为这个线性组合的系数（注意这里的a1,a2,...,am是向量，不是单一的数）

2.线性表示

给定向量组A：a1,a2,...,am和向量b，若有一组数λ1,λ2,...λm，使b=λ1a1+λ2a2,...,λmam，则向量b是向量组A的线性组合，称向量b能由向量组A线性表示

向量b能由向量组A线性表示==方程组x1a1+x2a2,...,xmam=b有解==(R(a1,a2,...,am)=R(a1,a2,...,am, b))

若有两个向量组A和B，若B中的每个向量都能由向量组A线性表示，则称向量组B能由向量组A线性表示

向量组B能由向量组A线性表示==矩阵方程(a1,a2,...,am)X=(b1,b2,...,bl)(AX=B)有解==(存在矩阵Km*l，使得B=AK)==（R(A)=R(A,B)）

注：R(B)<=R(A)

3.向量组等价

若向量组A与向量组B能互相线性表示，则称这两个向量组等价

向量组A与向量组B等价==(R(A)=R(B)=R(A,B))

三.例题解析

题型一：向量的运算

题型二：向量线性表示问题

设向量组B：β1,β1,...,βs可以由向量组A：α1,α2,..,αt线性表示，向量y可以由向量组B线性表示，试证明：向量y也可由向量组A线性表示

证明：

设A=(α1,α2,..,αt)，B=(β1,β1,...,βs)，则由向量组B可由向量组A线性表示可得存在矩阵K使得B=AK，又y可以由向量组B线性表示，可得y=Bx

故y=AKx=A(Kx)，所以y也可以由向量组A线性表示

该结论表示了向量组线性表示具有传递性

题型三：向量组的线性表示问题

例一：

任一n维向量均可由n维向量组A：α1,α2,..,αt线性表示的充要条件是n维单位坐标向量组B：e1,e2,...,en可由A线性表示

思路：

n维单位坐标向量ei是第i个元素为1，其余元素为0的n维向量，即为单位矩阵E的第i个列向量（i=1,2,...,n）

证明：

必要性：

因为任一n维向量均可由向量组A线性表示，所以向量组B中任一向量ei（i=1,2,...,n）均可由向量组A线性表示，故向量组B可由向量组A线性表示

充分性：

设A=(α1,α2,..,αt)，B=(e1,e2,...,en)，则R(B)=n，向量组B可以由向量组A线性表示，所以R(A)>=R(B)=n，又因为R(A)<=矩阵A的列数=n，所以R(A)=n

于是对于任何一个n维向量β，有n=R(A)<=R(A,β)<=矩阵(A,β)的行数n

故R(A)=R(A,β)=n

所以向量β能由向量组A线性表示

例二：

设B是由矩阵A经初等行变换得到的矩阵，证明A与B的列向量有完全相同的线性关系，即k1a1+k2a2+...+kmam=0当且仅当有k1b1+k2b2+...+kmbm=0，其中ai和bi分别为A和B的列向量

证明：

考虑线性方程组Ax=0与Bx=0，因为B是由A经初等行变换得到的，所以Ax=0与Bx=0同解

所以当Ak=0试，有Bk=0，即k1b1+k2b2+...+kmbm=0，反之也成立

题型四：由线性表示关系确定参数

向量组的线性相关性

线性相关（无关）->定义、判定、结论

一.线性相关、线性无关

1.线性相关

给定向量组A：a1,a2,...,am，若存在不全为零的数k1,k2,...,km，使k1a1+k2a2+...+kmam=0，则称向量组A是线性相关的（注意是m个向量，即m个未知数）

充要条件为齐次线性方程x1a1+x2a2+...+xmam=0有非零解

矩阵A=(a1,a2,...,am)的秩R(A)<m，即行列式|A|=0

2.线性无关

若k1=k2=...=km=0，则称向量组A是线性无关的

充要条件为齐次线性方程x1a1+x2a2+...+xmam=0只有零解

矩阵A的秩R(A)=m，即行列式|A|!=0

二.线性相关、无关的重要结论

1.向量组A：a1,a2,...,am（m>=2）线性相关，也就是在向量组A中至少有一个向量能由其余m-1个向量线性表示

2.含有零向量的向量组必是线性相关组

3.若向量组中有两个向量成比例，则该向量组必为线性相关组

4.n维单位坐标向量必线性无关

5.若m维向量组A线性相关，则m+1维向量组B也线性相关，若向量组B线性无关，则向量组A也线性无关

（部分相关，整体相关；整体无关，部分无关）

6.m个n维向量构成的向量组，当维数n小于向量个数m时一定线性相关（R(A)<=min{m,n}，所以R(A)必定小于m，小于未知量的个数，必定为线性相关），n+1个n维向量一定线性相关（n*n+1矩阵，n<n+1，即R(A)必定小于未知量n+1）

7.设向量组Aa1,a2,...,am线性无关，向量组Ba1,a2,...,am,b线性相关，则向量b必能由向量组A线性表示，且表达式是唯一的

三.例题解析

题型一：判断向量组的线性相关性

判断抽象向量组的线性相关性时，有以下三种思路：

1.定义法

即设k1a1+k2a2+...+kmam=0，考察k1,k2,...,km是否全为0

2.表示矩阵法

即若m个向量构成的向量组A线性无关，有AX=B，则B线性无关==(R(X)=m)，B线性相关==(R(X)<m)

3.利用相关结论证明

题型二：已知线性相关性求参数的问题

两个向量线性相关时，它们的对应分量成比例

利用线性相关的定义列出等式，转化为求方程组解的问题，若系数矩阵|A|=0，则线性相关，若|A|!=0，则线性无关

题型三：线性相关性与线性表示相关问题

设向量组a1,a2,a3线性相关，向量组a2,a3,a4线性无关。a1能否由a2，a3线性表示？a4能否由a1，a2，a3线性表示？

因为a1,a2,a3线性相关，所以有不全为0的数k1,k2,k3，使k1a1+k2a2+k3a3=0，若k1=0，则k2和k3不全为0，并且k2a2+k3a3=0，所以a2,a3线性相关，从而a2,a3,a4也线性相关，矛盾，所以k1!=0

从而有a1=(-k2/k1)a2+(-k3/k1)a3，所以a1可由a2和a3线性表示

a4不能由a1,a2,a3显现表示

若a4可以由a1,a2,a3线性表示，则有一组数k1,k2,k3使a4=k1a1+k2a2+k3a3，而a1可以由a2和a3线性表示，从而有一组数l2,l3，使a1=l2a2+l3a3，从而有a4=k1(l2a2+l3a3)+k2a2+k3a3=(k1l2+k2)a2+(k1l3+k3)a3，所以a4能由a2和a3表示，因此有基础解系，a2,a3,a4线性相关，矛盾

所以a4不能由a2和a3表示

题型四：与矩阵相关的向量组线性关系问题

用线性无关的定义及分块矩阵的知识将问题转化为熟悉的矩阵方阵问题

题型五：线性相关性常用结论证明

利用定义来讨论向量组的线性相关性是一种常用方法

向量组的秩

一.最大无关组

若向量组A中能选出r个向量a1,a2,..,ar线性无关，而向量组A中任意r+1个向量（A中有r+1个向量）都线性相关，则a1,a2,...,ar称为向量组A的一个最大线性无关向量组（最大无关组）

若a1,a2,...,ar是向量组A的一个部分组，且向量组a1,a2,...,ar线性无关，向量组A的任一向量都能由a1,a2,...,ar线性表示，则a1,a2,...,ar是向量组A的一个最大无关组

结论：

1.任意向量组都和它的最大无关组等价

2.同一向量组的任意两个最大无关组等价

3.两个等价的线性无关的向量组所含向量个数相同

4.一向量组的任一两个最大无关组所含向量个数相同

5.线性无关向量组的最大无关组是它本身

注：向量组的最大无关组不是唯一的

二.向量组的秩、矩阵的秩

1.向量组的秩

向量组A的最大无关组所含向量的个数r称为向量组A的秩

若向量组A的秩为r，则A中任意r个线性无感的向量均构成A的一个最大无关组，等价的向量组有相同的秩

2.矩阵的秩

矩阵的秩=列向量组的秩=行向量组的秩

任一矩阵的行秩与列秩相等

联系：

若Dr是矩阵A的一个最高阶非零子式，则Dr所在的r列即是A的列向量组的一个最大无关组，Dr所在的r行即是行向量组的一个最大无关组

3.向量组的线性表示与向量组的秩的关系

向量组b1,b2,...,bl能由向量组a1,a2,...,am线性表示的充分必要条件是R(a1,a2,...,am)=R(a1,...,am,b1,...,bl)

若向量组B能由向量组A线性表示，向量组B和A的秩分别表示为RB和RA，则RB<=RA

三.例题解析

题型一：求向量组的秩

矩阵的秩等于它的行向量组的秩，也等于它的列向量组的秩

一般使用反证法和定义法

向量组a1,a2,...,an的秩为r2，在其中任取m个向量β1,β2,...,βm，该向量组的秩为r1，则r1>=r2+m-n

题型二：向量组的秩与向量组的线性表示的关系

设n维列向量组a1,a2,...,am(m<n)线性无关，则n维列向量组b1,b2,...,bm线性无关的充分必要条件为矩阵A=(a1,a2,...,am)与矩阵B(b1,b2,...,bm)等价

讨论n维度向量组a1,a2,...,as的线性相关性，将其转化为方程组Ax=0是否有非零解，向量组a1,a2,...,as线性相关==Ax=0有非零解==R(A)<=min{n,s}

题型三：已知向量组的秩或线性关系讨论未知参数

一般利用非齐次线性方程组有解则其系数矩阵与增广矩阵的秩相等，或者利用最大无关组与原向量组等价的性质，将B由A线性表示这一条件，转化为由A的最大无关组表示

线性方程组的解的结构

一.齐次线性方程组解的性质与结构

1.性质

若x1,x2为方程组Ax=0的解，则x1+x2也是Ax=0的解

若x为方程组Ax=0的解，k为任意实数，则kx也是Ax=0的解

2.基础解系

齐次线性方程组的解集的最大无关组称为该齐次方程组的基础解系

设m×n的矩阵A的秩R(A)=r，则n元齐次线性方程组Ax=0的解集S的秩Rs=n-r，n元齐次线性方程组Ax=0的任意n-R(A)个线性无关的解都可构成它的基础解系

3.通解

若X1,X2,..,Xn-r是Ax=0的基础解系，则方程组Ax=0的任一解向量都可由X1,X2,...,Xn-r线性表示，且Ax=0的通解是k1X1+k2X2+...+Kn-rXn-r，其中k1,k2,...,kn-r是任意常数

二.非齐次线性方程解的性质与结构

1.性质

若X1,X2是非齐次线性方程组Ax=b的解，则X1-X2是对应的齐次线性方程组Ax=0的解

若X1是方程组Ax=b的解，X2是方程组Ax=0的解，则X1+X2是方程组Ax=b的解

2.通解

若X*是非齐次线性方程组Ax=b的特解，X1,X2,...,Xn-r是对应的齐次线性方程组Ax=0的基础解系，则方程组Ax=b的任一解均可表示为以上的线性组合，且方程组Ax=b的通解为X*+X1+...+Xn-r，其中k1,k2,...,kn-r是任意常数

三.例题解析

题型一：求具体齐次线性方程组的解

解齐次线性方程组的一般步骤：

1.将系数矩阵化为行最简矩阵

2.写出同解方程组

3.确定未知量，找出基础解系

4.写出通解

题型二：由齐次线性方程组的性质确定齐次线性方程组的解

n元齐次线性方程组Ax=0的任意n-R(A)个线性无关的解都可构成它的基础解系

题型三：求非齐次线性方程组的解

设三阶矩阵A=(a1,a2,a3)有3个不同的特征值，且a3=a1+2a2，证明R(A)=2

设A的特征值为λ1,λ2,λ3，因为A有三个不同的特征值，所以A可以相似对角化，即存在可逆矩阵P，使得(P^-1)AP为三阶矩阵

因为三个特征值两两不相同，则有R(A)>=2，又因为a3=a1+2a2，所以a1,a2,a3线性相关，因此R(A)<3，所以R(A)=2

若β=a1+a2+a3，求方程组Ax=β的通解

因为R(A)=2，所以Ax=0的基础解系含一个线性无关的解向量

由a3=a1+2a2，可得一个基础解系为(1,2,-1)T，所以Ax=0的通解为x=k(1,2,-1)T（k∈R）

由β=a1+a2+a3=A(1,1,1)T，可得Ax=β的一个特解为(1,1,1)T

所以Ax=β的通解为x=k(1,2,-1)T+(1,1,1)T（k∈R）

题型四：已知方程组的解，反求方程组

对于已知方程组的解反求原方程组的问题，首先应该搞明白方程组有多少个未知数，多少个方程

题型五：与方程组有关的应用

题型六：求解含参数的线性方程组

求解线性方程组最本质的思想是得到与原方程组同解的更简单的方程组，从而求解

对系数矩阵作初等变换可保证同解性，即方程组Ax=β和PAx=Pβ（P可逆）是同解方程组，所以系数矩阵所作的初等行变换只能是初等行变换

向量空间

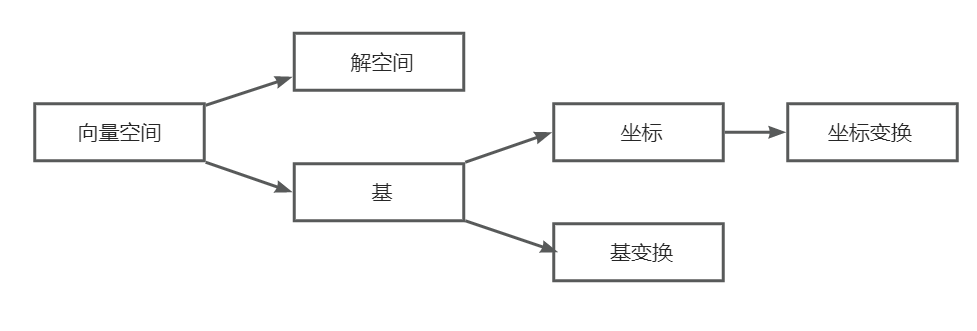
一.向量空间的相关概念

1.向量空间

若V是n维向量的非空集合，并且V对于向量的加法和数乘两种运算封闭，则称V是向量空间

封闭：若a∈V，b∈V，则a+b∈V，若a∈V，λ∈R，则λa∈V

2.解空间

齐次线性方程组的解集S={x|Ax=0}是一个向量空间，称为齐次线性方程组的解空间

3.向量生成空间

由向量组a1,a2,...,am生成的向量空间为L={x=k1a1+k2a2+...+kmam|k1,k2,...,km∈R}

设V1是由向量组a1,a2,...,am生成的向量空间，V2是由向量组b1,b2,...,bn生成的向量空间，则(V1=V2)==向量组a1,a2,...,am与向量组b1,b2,...,bn等价

4.子空间

设有向量空间V1及V2，若V1是V2的子集，则称V1是V2的子空间，任一由n维向量所组成的向量空间V都是R^n的子空间

5.向量空间的基

若向量空间V的r个向量a1,a2,...,ar满足

（一）a1,a2,...,ar线性无关

（二）V中任一向量都可由a1,a2,...,ar线性表示，则向量组a1,a2,...,ar称为向量空间的一个基，r称为向量空间的维数，并称V为r维向量空间

如果V是由向量组a1,a2,...,as生成的向量空间，则V的维数等于向量组a1,a2...,as的秩，向量组a1,a2,...,as的一个最大无关组是V的一个基

6.坐标

若a1,a2,...,ar是r维向量空间V的一个基，则V中任一向量x可唯一表示为x=k1a1+k2a2+...+krar，数组k1,k2,...,kr称为向量x在基a1,a2,...,ar的坐标

一般在R^n中取单位坐标向量e1,e2,...,en为基，则任一向量x=(x1,x2,...,xn)=x1e1+x2e2+...+xnen

二.过度矩阵

此处介绍三维

R^3中的基a1,a2,a3到基b1,b2,b3的基变换公式为(b1,b2,b3)=(a1,a2,a3)P，若记A=(a1,a2,a3)，B=(b1,b2,b3)，则P=(A^-1)B为从基a1,a2,a3到基b1,b2,b3的过渡矩阵

令P^-1=B^-1A，则任一向量在a1,a2,a3下的坐标y到其在b1,b2,b3下的坐标z的坐标变换公式为z=P-1y

注：过渡矩阵一定是可逆的

三.例题解析

题型一：判断向量集合是否构成向量空间

验证向量集合是向量空间需首先验证集合非空，再验证加法和数乘封闭即可

题型二：涉及基于坐标的问题

一般利用矩阵取逆来求坐标，也可将β=x1a1+x2a2+...+xrar写成线性方程组，再解出x1,x2,...,xr的值

由向量组A生成的向量空间的维数等于向量组A的秩

题型三：求过渡矩阵

解题时利用逆矩阵和初等行变换

知识总结

一.关于判断向量组线性相关性的小结

给出向量组a1,a2,...,an，判断其是否线性相关主要利用定义，利用矩阵的秩，利用行列式，利用向量组的等价性

1.定义法

假设有一组数k1,k2,...,kn，使k1a1+k2a2+...+knan=0成立，若k1,...,kn全为零，则a1,a2,...,an线性相关

2.矩阵秩法

求矩阵A=(a1,a2,...,an)的秩，当R(A)=n时，a1,a2,...,an线性无关，当R(A)<n时，a1,a2...,an线性相关

3.行列式法

向量组的个数与向量组的维数相同时（方阵）可利用行列式来判断其线性相关性，当|A|=|a1,a2,...,an|=0时，向量组a1,a2...,an线性相关，当|A|=|a1,a2,...,an|!=0时，向量组a1,a2...,an线性无关

4.等价性

找一个与向量组a1,a2,...,an等价的并且比较容易判定线性相关性的新向量组，讨论新向量组的线性相关性，从而可判断向量组a1,a2,...,an的线性相关性

二.关于求向量组的秩的小结

求向量组的秩通常利用初等变换、利用向量组的等价性、利用向量组秩的定义等方法

1.初等变换法

给定向量组a1,a2,...,an，可将它们组成的矩阵作初等变换化成行阶梯型矩阵后可判断其秩

2.等价性

找出一个与向量组等价的新向量组，因为等价的向量组有相同的秩，新向量组的秩即等于原向量组的秩

3.定义法

找出向量组的一个最大线性无关组，其向量个数就是向量组的秩

三.关于求向量组的最大无关组的小结

1.利用初等变换求向量组的最大无关组

2.逐一选择求向量组的最大无关组

四.关于向量空间的基和维数的小结

向量空间是对于向量的加法和数乘都封闭的特殊的向量组，将向量空间视为向量组，则向量空间的基和维数分别对应向量组的最大无关组和秩，向量空间的基并不是唯一的，即在一个向量空间中可能找出多组基

五.关于线性方程的小结

1.齐次线性方程组Ax=0的解的集合构成一个向量空间称为解空间，其基础解系实际上就是解空间的一个基，方程组Ax=0的每一个解都可由其基础解系线性表示

2.非齐次线性方程组Ax=b的任一解都可由Ax=b的一个特解和对应的方程组Ax=0的某一解表示，只要找到Ax=0的通解和Ax=b的特解就可得到Ax=b的通解

言尽于此，不足之处欢迎各位一起讨论和交流。