2.6 多元线性回归

1.特征：

1).单特征：

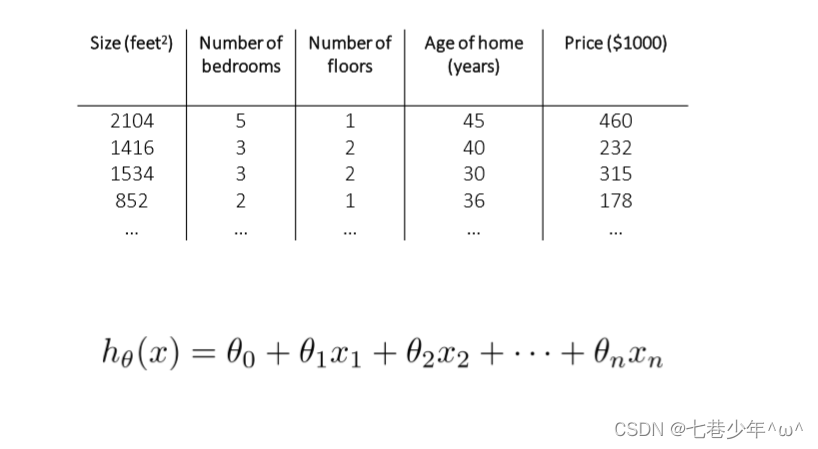
在这里插入图片描述

2).多特征：

在这里插入图片描述

有多少个特征就有多少个未知数x

2.多元线性回归模型的使用场景：

当Y值的影响因素不是唯一时，采用多元线性回归。
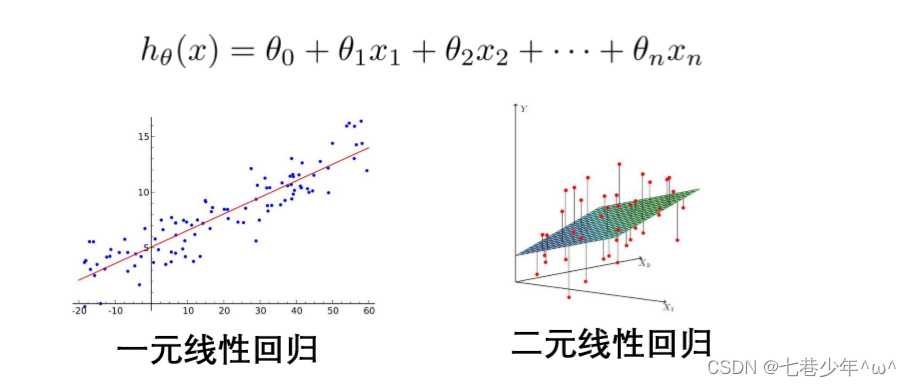
在这里插入图片描述

3.梯度下降法求解多元线性回归

1).公式：

在这里插入图片描述

①.求导之后的公式：
在这里插入图片描述

4.实战1：梯度下降法—多元线性回归：

1).CSV中的数据：

以一家快递公司送货为例：X1-运货里程 X2-运货次数 Y：总运输时间
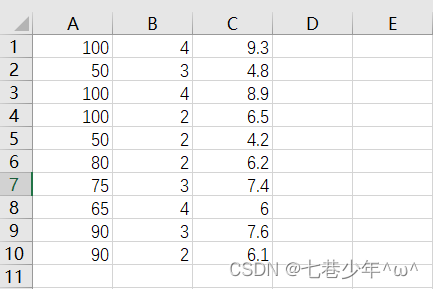
在这里插入图片描述

2).代码

import numpy as np
import matplotlib.pyplot as plt

# 加载数据
data = np.loadtxt('D:\\data\\Delivery.csv', delimiter=',')
# 切分数据
x_data = data[:, :-1]
y_data = data[:, -1]

# 学习率learning rate
lr = 0.0001

# 参数
theta0 = 0
theta1 = 0
theta2 = 0

# 最大迭代次数
epochs = 1000


# 代价函数：最小二乘法
def computer_error(x_data, y_data, theta0, theta1, theta2):
    totalerror = 0
    for i in range(0, len(x_data)):
        totalerror += ((theta1 * x_data[i, 0] + theta2 * x_data[i, 1] + theta0) - y_data[i]) ** 2
    return totalerror / float(len(x_data)) / 2


# 梯度下降法
def gradient_descent(x_data, y_data, theta0, theta1, theta2, lr, epochs):
    # 数据集的总数量
    m = float(len(x_data))

    # 循环epochs次
    for i in range(epochs):
        grad_theta0 = 0
        grad_theta1 = 0
        grad_theta2 = 0

        for j in range(0, len(x_data)):
            # 梯度的计算
            grad_theta0 += (1 / m) * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
            grad_theta1 += (1 / m) * x_data[j, 0] * (
                    (theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
            grad_theta2 += (1 / m) * x_data[j, 1] * (
                    (theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
        # 更新grad_theta0,grad_theta1,grad_theta2
        theta0 = theta0 - lr * grad_theta0
        theta1 = theta1 - lr * grad_theta1
        theta2 = theta2 - lr * grad_theta2

    return theta0, theta1, theta2


print('初始参数：theta0={0}，theta1={1}，theta2={2},error={3}'.format(theta0, theta1, theta2,
                                                               computer_error(x_data, y_data, theta0, theta1, theta2)))

theta0, theta1, theta2 = gradient_descent(x_data, y_data, theta0, theta1, theta2, lr, epochs)

print('结果参数：theta0={0}，theta1={1}，theta2={2},error={3}'.format(theta0, theta1, theta2,
                                                               computer_error(x_data, y_data, theta0, theta1, theta2)))

ax = plt.figure().add_subplot(111, projection='3d')
x0 = x_data[:, 0]
x1 = x_data[:, 1]
ax.scatter(x0, x1, y_data, c='r', marker='o', s=30)

# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = theta0 + theta1 * x0 + theta2 * x1

# 画3D图像
ax.plot_surface(x0, x1, z)

# 设置坐标轴
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Delivery')
ax.set_zlabel('Time')

# 显示图像
plt.show()

3).结果展示：

①.数据

在这里插入图片描述

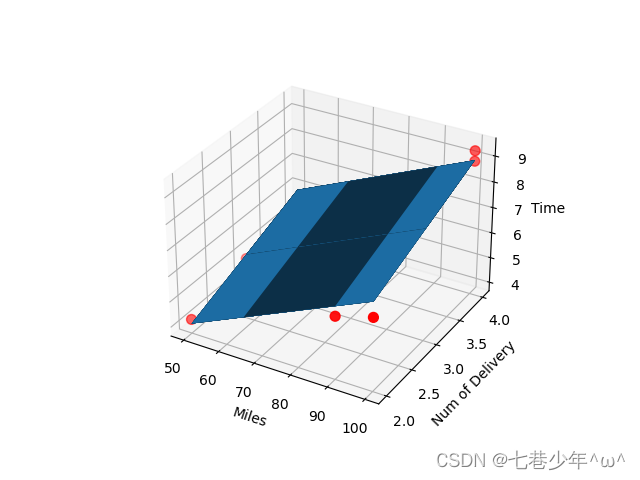
②.图像
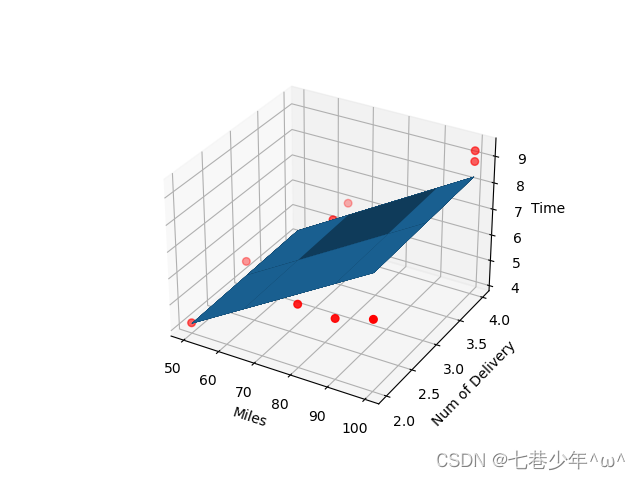
请添加图片描述

5.实战2： sklearn—多元线性回归：

1).CSV中的数据：

以一家快递公司送货为例：X1-运货里程 X2-运货次数 Y：总运输时间
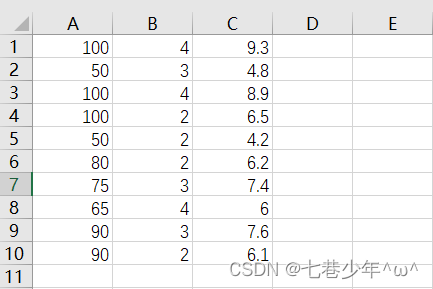
在这里插入图片描述

2).代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

# 加载数据
data = np.loadtxt('D:\\data\\Delivery.csv', delimiter=',')
x_data = data[:, :-1]
y_data = data[:, -1]

# 创建模型
model = linear_model.LinearRegression()
# 拟合模型
model.fit(x_data, y_data)

# 回归系数
coeff = model.coef_
print('回归系数：', coeff)

# 截距
intercept = model.intercept_
print('截距：', intercept)

# 预测数据
x_test = [[102, 4]]
predict = model.predict(x_test)
print('预测数据', predict)

# 创建画布
ax = plt.figure().add_subplot(111, projection='3d')

# 切分数据
x0 = x_data[:, 0]
x1 = x_data[:, 1]

# 画散点图
ax.scatter(x0, x1, y_data, c='r', marker='o', s=50)

# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)

z = coeff[0] * x0 + coeff[1] * x1 + intercept

# 画3D图
ax.plot_surface(x0, x1, z)

# 设置坐标轴
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Delivery')
ax.set_zlabel('Time')

# 显示图像
plt.show()