目录
- 传播与社会动力学(1)
- 传播
- simplicial complexes
- hypergraphs
传播与社会动力学(1)
模拟人类行为的动态过程一直是许多研究的焦点,其中社会关系和交互通常被认为是一种潜在结构,是高阶方法的天然试验场。
传播
网络传播过程时建立在经典的流行病学模型基础上的。经典的流行病学模型主要可分为两大类,即
- SIR (Susceptible–Infected–Recovered)模型。
- SIS (Susceptible–Infected–Susceptible)模型。
这两个模型中,易感个体(S)可通过与感染个体(I)相互作用而感染。前者个体在一定时间后获得对再次感染的免疫力,这些免疫个体即(R)不再参与传播,因此该模型也被称为吸收状态(absorbing state);后者个体在 S 和 I 之间相互切换,最终达到一个非零的稳定状态。
+++++++++++++++++
基于这两个基础模型也有许多变形,及相关处理方法(如:平均场法、异构平均场法和微观马氏链法),在此不赘述。
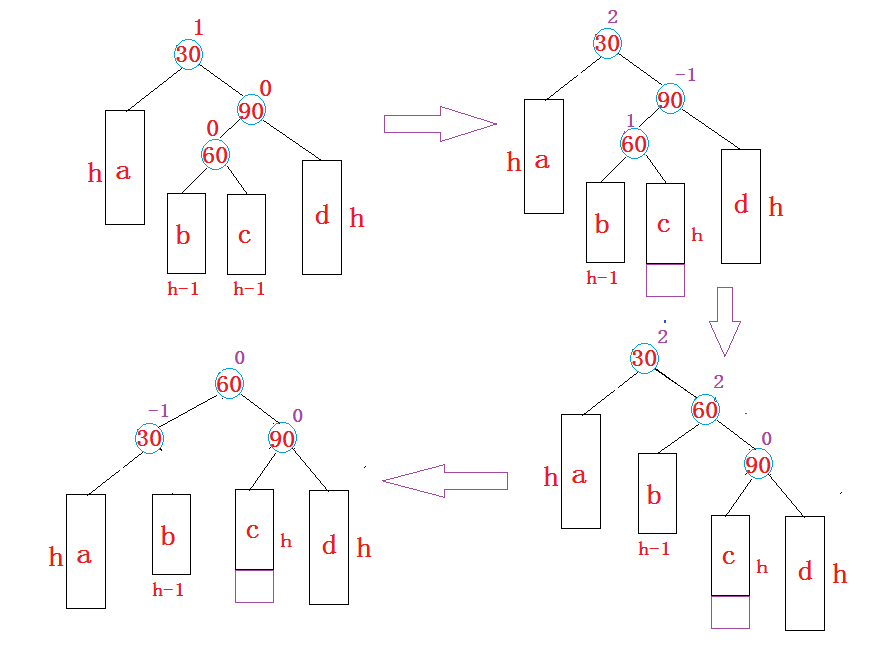
simplicial complexes
在simplicial contagion model1 中,simplicial complexes 被用来表示传染动态发生在其之上的社会结构。考虑每个组交互中包含的所有子交互,该模型的动态依赖于不同的感染渠道(单纯型)。通过这些渠道,以不同的传播率发生传染。

通过一组控制参数
β
i
,
i
=
1
,
⋯
,
D
\beta_{i}, i = 1, \cdots,D
βi,i=1,⋯,D 等对
D
D
D 阶 SIS 型-模型进行控制,该参数即单位时间的感染概率。平均场法很适合用于此类高阶情形,感染节点的静止密度演化的一般方程如下:
ρ
˙
(
t
)
=
−
μ
ρ
(
t
)
+
∑
d
=
1
D
β
d
[
k
d
]
ρ
d
(
t
)
(
1
−
ρ
(
t
)
)
.
\dot{\rho}(t) = - \mu \rho(t) + \sum_{d=1}^{D} \beta_{d}[k_{d}]\rho^{d}(t) (1 - \rho(t)).
ρ˙(t)=−μρ(t)+d=1∑Dβd[kd]ρd(t)(1−ρ(t)). 该方法证实了在synthetic random simplicial complexes 上得到的结果:在具有均匀度分布特征的社会结构上,稳态动态、位置和过渡性质可以被分析预测。
hypergraphs
与 simplicial complexes 相比,超图可以用来描述只发生在组中的交互,从而解除了必须包括组内所有子交互的限制。因此,超边可以有效地用于表示集群或社区。超图也被用来模拟协作网络中的知识扩散。将社区建模为超边的想法中,使用超图的节点来表示个人,使用超边来表示节点所属的不同社区。作者2研究了一个SIS模型在连续时间马尔可夫链形式下的超图上的行为,其中感染和恢复都服从泊松过程。
基于 SIS 型-模型的超图演化的一般方程: ρ ˙ k ( t ) = − μ ρ k ( t ) + β k ( 1 − ρ k ( t ) ) k Θ d − 1 . \dot{\rho}_{k} (t) = - \mu \rho_{k} (t) + \beta_{k}(1 - \rho_{k}(t)) k \Theta^{d -1}. ρ˙k(t)=−μρk(t)+βk(1−ρk(t))kΘd−1. 此外,基于类似的 SIS 的框架,可将临界质量动力学明确地包含在传染过程中,从而推广了上述传染过程。事实上,实验已经显示了启动社会变革所需的临界质量水平的不同值,即通过承诺的少数人将现有的平衡恢复到新的平衡。
基于 SIR 模型的不同扩展引入超图。将个体置于一个谣言传播的框架中,个体分为三个标准类别:无知(S)、传播者(I)和扼杀者(R)。

I. Iacopini, G. Petri, A. Barrat, V. Latora, Simplicial models of social contagion, Nature Commun. 10 (1) (2019) 2485. ↩︎
Á. Bodó, G.Y. Katona, P.L. Simon, SIS epidemic propagation on hypergraphs, Bull. Math. Biol. 78 (4) (2016) 713–735. ↩︎