参考文献:
[1]夏澍,周明,李庚银.分布式电源选址定容的多目标优化算法[J].电网技术,2011,35(09):115-121.
[2] Ye Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, “PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum],” IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87.
[3] Ye Tian, Weijian Zhu, Xingyi Zhang, and Yaochu Jin, “A practical tutorial on solving optimization problems via PlatEMO,” Neurocomputing, 2023, 518: 190-205.
结合实际的算例,分析PlatMEO工具箱求解电力系统多目标优化领域的方法。
1.基本原理
在综合考虑网损、电压质量和电流质量 3 个指标的基础上,建立了分布式电源选址定容的多目标决策模型,并提出了一种改进多目标微分进化算法(improved differential evolution for multiobjective optimization,IDEMO)。该算法引入混沌搜索策略以提高初始种群利用率,采用控制参数调整策略以克服算法对控制参数依赖性强的缺点,利用动态拥挤距离排序策略使得帕累托解集分布更加均匀,从而为最终决策提供了优良的候选方案。以上述算法求得的帕累托最优解集为决策矩阵,使用基于熵的序数偏好方法对最优解集进行排序,得到最终决策方案。在 IEEE-33 节点系统上对所提方法进行了测试,并从外部解、C 指标和 S 指标 3 方面与其他 3 种多目标优化算法进行了比较,验证了所提算法具有良好的搜索性能。最后评价了所选方案的有效性。
1.1 目标函数
本文评估 DG 效益的指标选用系统网损指标、节点电压指标和线路电流指标。
1)系统网损指标。
DG 接入电网能够带来一个明显的节能效益就是降低网损,提高能源利用率,文献[4]提出了系统网损评价指标,其定义如下:

2)节点电压指标。
DG 能够改善电压分布情况,使电压偏移维持在较小范围内。文献[12]提出了一个电压偏移指标,即计算首节点电压与电网其他节点电压偏差的平均值,具体计算公式如下:
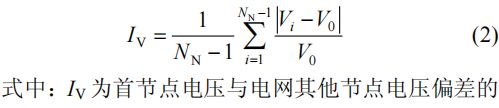

3)线路电流指标。
DG 接入电网可能会减少部分线路电流,但也可能会增加线路电流,因此需要对线路电流水平进行评价。一般采用的指标是线路热稳定裕度,即系统所有线路中最大载流量,其定义如下:

式中 x 为优化方案。模型(6)即为寻求使得3个目标最优的方案。由于各个目标之间存在冲突,无法保证所有目标值同时达到最小,因此只能得到一组帕累托最优解集(Pareto solution set),其特点为至少存在一个目标优于其他所有解。
1.2 约束条件
DG 选址定容问题的约束包括投资约束和系统运行约束,分别为:


2. MOCDE算法与PlatEMO工具箱
platEMO是安徽大学生物智能与知识发现(BIMK)研究所编写的一款基于MATLAB的多目标优化工具,为新入门的同学或者开发者提供了很大的便利,其今年已经发布到PlatEMO 2.0版本了。这款工具主要具有以下的几个特点:
1.完全由MATLAB开发,不需要任何其它库。
2.包括现有的90个流行的多目标优化算法,包括遗传算法、差分进化、粒子群优化、模因算法、分布估计算法和基于代理模型的算法。其中大多数是2010年以后在顶级期刊上发表的代表性算法。
3.用户可以显示各种图形,包括结果的pareto front,真实的pareto front等等。
4.强大友好的GUI,可以不用编辑任何代码。
5.可以直接生成Excel或者LaTex。
如果要用到GUI界面,PlatEMO工具箱要求MATLAB版本在 R2020b 或以上及安装了并行计算工具箱和统计与机器学习工具箱。
如果不需要使用GUI界面,只需要MATLAB R2018a或以上的版本即可使用。
下面对该工具箱的通过代码调用的方式进行简单介绍,并分析如何借助该工具箱求解优化问题。
2.1. 求解测试问题
用户可以以如下形式带参数调用主函数 platemo()来求解测试问题:
platemo('Name1',Value1,'Name2',Value2,'Name3',Value3,…);
其中所有可接受的参数列举如下:

'algorithm'表示待运行的算法,它的值可以是一个算法类的句柄,例如@GA。它的值还可以是形如{@GA,p1,p2,…}的单元数组,其中 p1,p2,… 指定了该算法中的参数值。例如以下代码用算法@GA 求解默认问题,并设置了该算法中的参数值:
platemo('algorithm',{@GA,1,30,1,30});'problem'表示待求解的测试问题,它的值可以是一个问题类的句柄,例如@SOP_F1。它的值还可以是形如{@SOP_F1,p1,p2,…}的单元数组,其中 p1,p2,… 指定了该问题中的参数值。例如以下代码用默认算法求解问题@WFG1,并设置了该问题中的参数值:
platemo('problem',{@WFG1,20});'N'表示算法使用的种群的大小,它通常等于最终输出的解的个数。例如以下代码用算法@GA 求解问题@SOP_F1,并设置种群大小为 50:
platemo('algorithm',@GA,'problem',@SOP_F1,'N',50);'M'表示问题的目标个数,它仅对一些多目标测试问题生效。例如以下代码用算法@NSGAII 求解具有 5 个目标的@DTLZ2 问题:
platemo('algorithm',@NSGAII,'problem',@DTLZ2,'M',5);'D'表示问题的变量个数,它仅对一些测试问题生效。例如以下代码用算法@GA 求解具有 100 个变量的@SOP_F1 问题:
platemo('algorithm',@GA,'problem',@SOP_F1,'D',100);'maxFE'表示算法可用的最大评价次数,它通常等于种群大小乘以迭代次数。例如以下代码设置算法@GA 的最大评价次数为 20000:
platemo('algorithm',@GA,'problem',@SOP_F1,'maxFE',20000);'maxRuntime'表示算法可用的最大运行时间,单位为秒。当 maxRuntime等于默认值 inf 时,算法将在 maxFE 次评价次数后停止;否则,算法将在maxRuntime 秒后停止。例如以下代码设置算法@GA 的最大运行时间为 10 秒:
platemo('algorithm',@GA,'problem',@SOP_F1,'maxRuntime',10);'save'表示保存的种群数,该值大于零时优化结果将被保存在文件中,该值小于零时优化结果将被显示在窗口中(参阅获取运行结果章节)。
· 'outputFcn'表示算法每代开始前调用的函数。该函数必须有两个输入和零个输出,其中第一个输入是当前的 ALGORITHM 对象、第二个输入是当前的 PROBLEM 对象。默认的'outputFcn'会根据'save'的值来保存或显示优化结果。
注意以上每个参数均有一个默认值,用户可以在调用时省略任意参数。
2.2 求解自定义问题
当不指定参数'problem'时,用户可以通过指定以下参数来自定义问题:
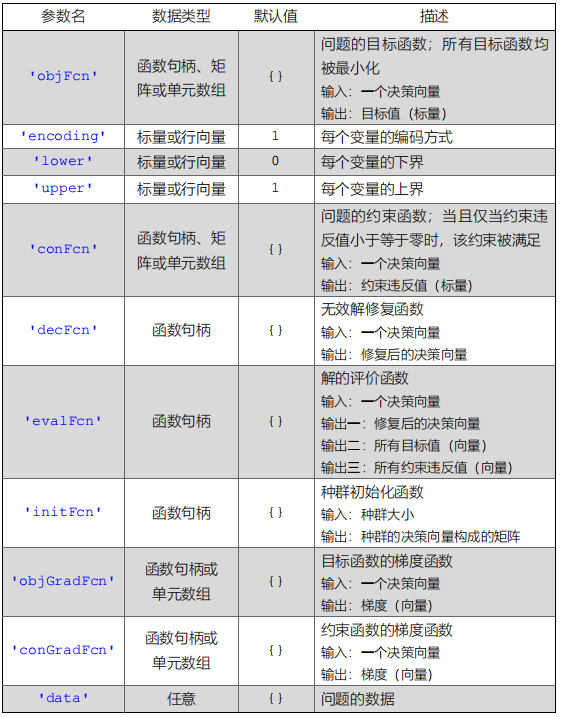
'objFcn'表示问题的目标函数,它的值可以是一个函数句柄(单目标)、矩阵(自动拟合出函数)或一个单元数组(多目标)。每个目标函数必须有一个输入和一个输出,其中输入是一个决策向量、输出是目标值。所有目标函数均被最小化。例如以下代码利用默认算法求解一个含有六个实数变量的双目标优化问题:
f1 = @(x)x(1)+sum(x(2:end));
f2 = @(x)sqrt(1-x(1)^2)+sum(x(2:end));
platemo('objFcn',{f1,f2},'D',6); ![]()
若一个目标函数是矩阵,则高斯过程回归会利用该矩阵自动拟合出一个函数,其中矩阵的每行表示一个样本、每列表示一个变量(除最后一列)或函数值(最后一列)。例如以下代码求解相同的问题,但目标函数是根据矩阵自动拟合出来的:
x = rand(50,6);
y1 = x(:,1)+sum(x(:,2:end),2);
y2 = sqrt(1-x(:,1).^2)+sum(x(:,2:end),2);
platemo('objFcn',{[x,y1],[x,y2]},'D',6); 'encoding'表示每个变量的编码方式,它的值可以是一个标量或行向量,且每维的值可以为 1(实数)、2(整数)、3(标签)、4(二进制数)或 5(序列编号)。算法针对不同的编码方式可能使用不同的算子来产生解。例如以下代码指定三个实数变量、两个整数变量以及一个二进制变量:
f1 = @(x)x(1)+sum(x(2:end));
f2 = @(x)sqrt(1-x(1)^2)+sum(x(2:end));
platemo('objFcn',{f1,f2},'encoding',[1,1,1,2,2,4]); 问题的变量数将根据'encoding'的长度自动确定。
'lower'和'upper'分别表示每个变量的下界和上界,它们的值可以是标量或行向量,且每维的值必须为实数。'lower'和'upper'的长度必须与'encoding'相同。例如以下代码指定搜索空间为 [0,1] × [0,9] 5:
f1 = @(x)x(1)+sum(x(2:end));
f2 = @(x)sqrt(1-x(1)^2)+sum(x(2:end));
platemo('objFcn',{f1,f2},'encoding',[1,1,1,2,2,4],...
'lower',0,'upper',[1,9,9,9,9,9]); 'conFcn'表示问题的约束函数,它的值可以是一个函数句柄(单约束)、矩阵(自动拟合出函数)或一个单元数组(多约束)。每个约束函数必须有一个输入和一个输出,其中输入是一个决策向量、输出是约束违反值。当且仅当约束违反值小于等于零时,该约束被满足。例如以下代码利用默认算法求解一个双目标优化问题,![]() :
:
f1 = @(x)x(1)+sum(x(2:end));
f2 = @(x)sqrt(1-x(1)^2)+sum(x(2:end));
g1 = @(x)1-sum(x(2:end));
platemo('objFcn',{f1,f2},'encoding',[1,1,1,2,2,4],...
'conFcn',g1,'lower',0,'upper',[1,9,9,9,9,9]);注意,等式约束必须转换为不等式约束来处理,详细方法可参阅参考文献[3]的 3.2 节。若一个约束函数是矩阵,则高斯过程回归会利用该矩阵自动拟合出一个函数,其中矩阵的每行表示一个样本、每列表示一个变量(除最后一列)或函数值(最后一列)。例如以下代码求解相同的问题,但约束函数是根据矩阵自动拟合出来的:
f1 = @(x)x(1)+sum(x(2:end));
f2 = @(x)sqrt(1-x(1)^2)+sum(x(2:end));
x = rand(50,6);
y = 1-sum(x(:,2:end),2);
platemo('objFcn',{f1,f2},'encoding',[1,1,1,2,2,4],...
'conFcn',[x,y],'lower',0,'upper',[1,9,9,9,9,9]);'decFcn'表示问题的无效解修复函数,它的值必须是一个函数句柄。该函数必须有一个输入和一个输出,其中输入是一个决策向量、输出是修复后的决策向量。例如以下代码限制 x1 为 0.1 的倍数:
f1 = @(x)x(1)+sum(x(2:end));
f2 = @(x)sqrt(1-x(1)^2)+sum(x(2:end));
g1 = @(x)1-sum(x(2:end));
h = @(x)[round(x(1)/0.1)*0.1,x(2:end)];
platemo('objFcn',{f1,f2},'encoding',[1,1,1,2,2,4],...
'conFcn',g1,'decFcn',h,'lower',0,'upper',[1,9,9,9,9,9]);'evalFcn'表示解的评价函数,它的值必须是一个函数句柄。该函数必须有一个输入和三个输出,其中输入是一个决策向量、第一个输出是修复后的决策向量、第二个输出是目标值向量、第三个输出是约束违反值向量。默认的'evalFcn'通过依次调用'decFcn'、'objFcn'和'conFcn'来评价解,而以下代码定义了一个新的'evalFcn'来同时进行解的修复、目标计算和约束计算:
function [x,f,g] = Eval(x)
x = [round(x(1)/0.1)*0.1,x(2:end)];
x = max(0,min([1,9,9,9,9,9],x));
f(1) = x(1)+sum(x(2:end));
f(2) = sqrt(1-x(1)^2)+sum(x(2:end));
g = 1-sum(x(2:end));
end接着,以下代码通过仅指定评价函数定义了相同的问题:
platemo('evalFcn',@Eval,'encoding',[1,1,1,2,2,4],...
'lower',0,'upper',[1,9,9,9,9,9]);'initFcn'表示种群初始化函数,它的值必须是一个函数句柄。该函数必须有一个输入和一个输出,其中输入是种群大小、输出是种群的决策向量构成的矩阵。默认的'initFcn'在整个搜索空间内随机产生初始解,而以下代码定义了一个新的'initFcn'以加速收敛:
q = @(N)rand(N,6);
platemo('evalFcn',@Eval,'encoding',[1,1,1,2,2,4],...
'initFcn',q,'lower',0,'upper',[1,9,9,9,9,9]);'objGradFcn'和'conGradFcn'分别表示目标函数和约束函数的梯度函数,它们的值可以是函数句柄或单元数组。每个梯度函数必须有一个输入和一个输出,其中输入是一个决策向量、输出是梯度。默认的梯度函数通过有限差分来估计梯度,而以下代码定义了一个新的'objGradFcn'以加速收敛并保证种群的多样性:
fg = @(x)[0,x(2:end)];
platemo('evalFcn',@Eval,'encoding',[1,1,1,2,2,4],...
'objGradFcn',fg,'lower',0,'upper',[1,9,9,9,9,9]);注意仅有少量算法会使用梯度信息。
'data'表示问题的数据,它可以是任意类型的常量。当指定'data'后,以上所有函数必须增加一个输入参数来接收'data'。例如以下代码求解一个旋转的单目标优化问题:
d = rand(RandStream('mlfg6331_64','Seed',28),10)*2-1;
[d,~] = qr(d);
f1 = @(x,d)sum((x*d-0.5).^2);
platemo('objFcn',f1,'encoding',ones(1,10),'data',d);除以上定义问题的方式之外,用户还能创建一个自定义问题对象并创建算法对象予以求解。例如以下代码利用算法@GA 和算法@DE 求解相同的问题:
d = rand(RandStream('mlfg6331_64','Seed',28),10)*2-1;
[d,~] = qr(d);
f1 = @(x,d)sum((x*d-0.5).^2);
PRO = UserProblem('objFcn',f1,'encoding',ones(1,10),'data',d);
ALG1 = GA();
ALG2 = DE();
ALG1.Solve(PRO);
ALG2.Solve(PRO); 2.3 输出参数
算法运行结束后得到的种群可以被显示在窗口中、保存在文件中或作为函数返回值。若按以下方式调用主函数:
[Dec,Obj,Con] = platemo(…);
则最终种群会被返回,其中 Dec 表示种群的决策向量构成的矩阵、Obj 表示种群的目标值构成的矩阵、Con 表示种群的约束违反值构成的矩阵。若按以下方式调用主函数:
platemo('save',Value,…);
则当 Value 的值为负整数时(默认情况),得到的种群会被显示在窗口中,用户可以在窗口中的 Data source 菜单选择要显示的内容。当 Value 的值为正整数 时 ,得到的种群会被保存在名为PlatEMO\Data\alg\alg_pro_M_D_run.mat 的 MAT 文件中,其中 alg 表示算法名、pro 表示问题名、M 表示目标数、D 表示变量数、run 是一个自动确定的正整数以保证不和已有文件重名。每个文件存储一个单元数组 result 和一个结构体 metric,其中 result 保存得到的种群、metric 保存指标值。算法的整个优化过程被等分为 Value 块,其中 result 的第一列存储每块最后一代时所消耗的评价次数、result 的第二列存储每块最后一代时的种群、metric 存储所有种群的指标值。
以上操作均由默认的输出函数@DefaultOutput 实现,用户可以通过指定'outputFcn'的值为其它函数来实现自定义的结果展示或保存方式。
2.4 编程实例
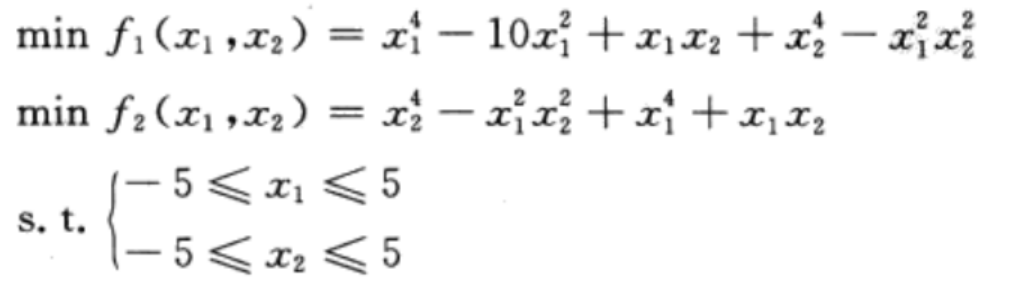
使用PlatEMO工具箱调用MODE算法求解上述优化问题的代码为:
f1 = @(x)(x(1)^4 - 10*x(1)^2 + x(1)*x(2) + x(2)^4 - (x(1)*x(2))^2);
f2 = @(x)(x(2)^4 - (x(1)*x(2))^2 + x(1)^4 + x(1)*x(2));
platemo( 'objFcn',{f1,f2},'D',2 , 'lower' , -5 , 'upper' , 5);运行结果如下:


3.编程思路分析
3.1相关参数和决策变量定义
表1 相关参数的定义
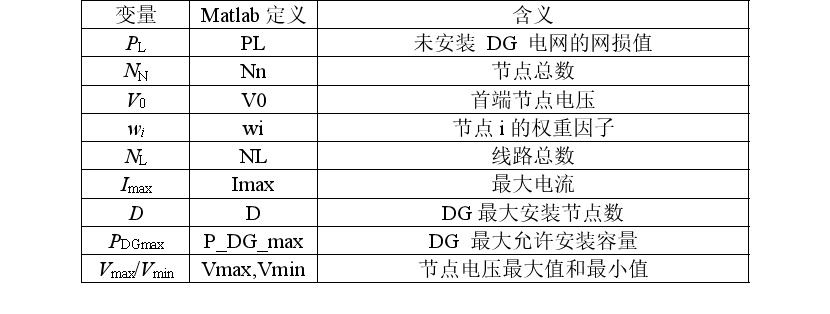
表2 决策变量的定义

3.2编程思路
根据对文献内容的解读,可以设计下面的编程思路:
步骤1:输入所需数据
这一步比较简单。算例分析用到的大部分数据可以从原文中找到,其他数据可以自己假设一下。然后将所有需要的数据,按照表1的定义格式输入即可。
步骤2:决策变量的设定
如表2所示,原文中共包含2个决策变量,均为1×D的变量,且在算例分析部分提到了最大DG安装节点数D为2个,因此可知文中涉及的优化问题维度为4,具体变量设置如下:
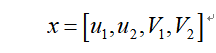
其中,优化变量x的1-2位为整数变量,3-4位为连续变量
步骤3:决策变量的上下界设定
按照步骤2中设定的决策变量,给定各个决策变量的上界UB和下界LB,如下所示:

步骤4:设定约束条件
文中所提约束条件为7-11,共五条约束,其中约束7可以用决策变量的上下限约束表示,功率平衡约束在潮流计算时即可考虑到,因此还需要对约束条件8,10和11进行设定,需要按照PlatEMO工具箱的要求改写成≤0的形式。

步骤5:设定修复函数
当生成的解不满足约束条件8时,还可以对该组解进行修复,令V2 = PDGmax - V1即可。
步骤6:设定目标函数
文中所提优化问题中包含3个目标函数,均为min形式,需按照工具箱要求的格式进行设定。
步骤7:调用platemo工具箱求解
设定好算法的决策变量维度、种群规模,最大迭代次数等其他参数,然后调用platemo函数求解上述优化问题。
步骤8:输出运行结果
参考文中的图表的格式,输出结果即可。
4.Matlab代码
%% 分布式电源选址定容的多目标优化算法复现代码
%% 添加路径
addpath(genpath('参数,目标函数和约束条件'))
%% 清空内存
clc
clear
close all
%% 参数设置
parameter;
%% 目标函数
f1 = @objfun1;
f2 = @objfun2;
f3 = @objfun3;
%% 优化变量上下限约束
UB = [33 , 33 , 2 , 2];
LB = [2 , 2 , 0 , 0];
%% 约束条件
g1 = @conFcn1;
g2 = @conFcn2;
g3 = @conFcn3;
%% 无效解的修复函数
h = @decFcn;
%% 求解优化问题
[Dec,Obj,Con] = platemo('algorithm',@MOEADDE, 'objFcn',{f1,f2,f3},'encoding', [2,2,1,1], 'lower' , LB , 'upper' , UB , 'conFcn', {g1,g2,g3} , 'decFcn' , h);
Dec(:,1:2) = round(Dec(:,1:2));
%% 展示运行结果
show_result;
以上仅为主函数部分的代码,完整论文复现的matlab代码可以从这个链接获取:
注意,运行程序需要matpower工具箱和platemo工具箱的支持,需要提前安装。
Matpower工具箱下载地址:
MATPOWER – Free, open-source tools for electric power system simulation and optimization
Platemo工具箱下载地址
BIMK/PlatEMO: Evolutionary multi-objective optimization platform (github.com)
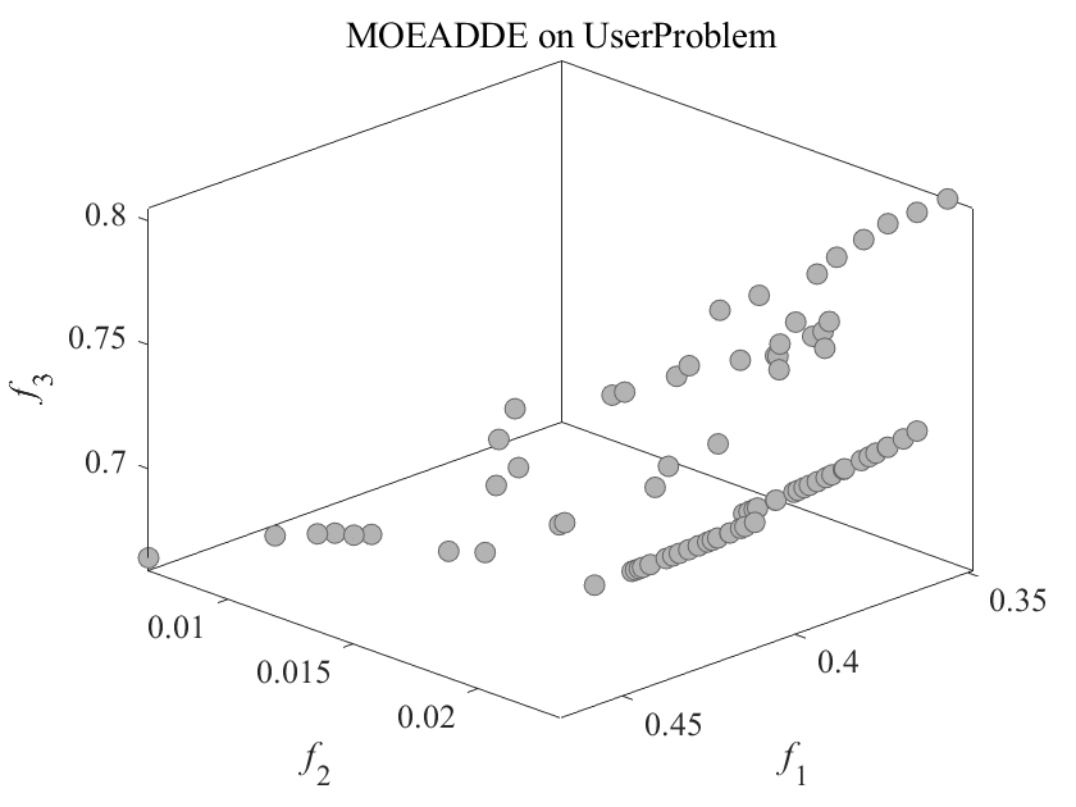
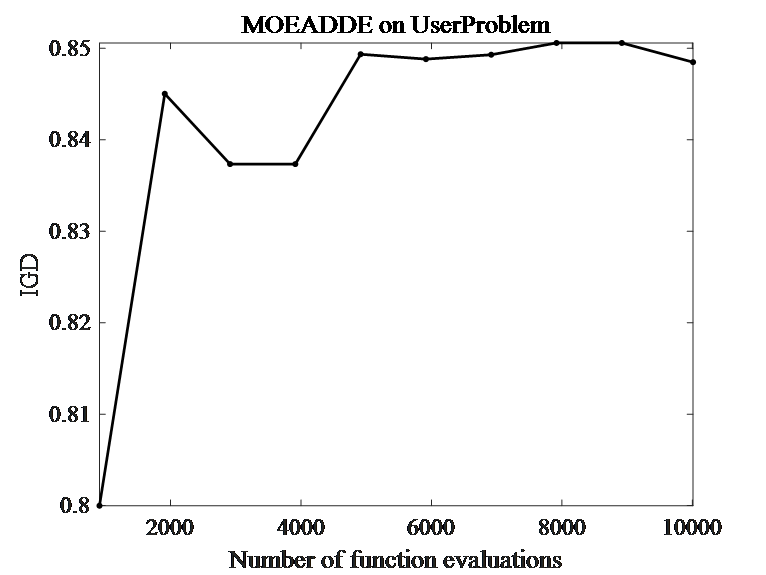
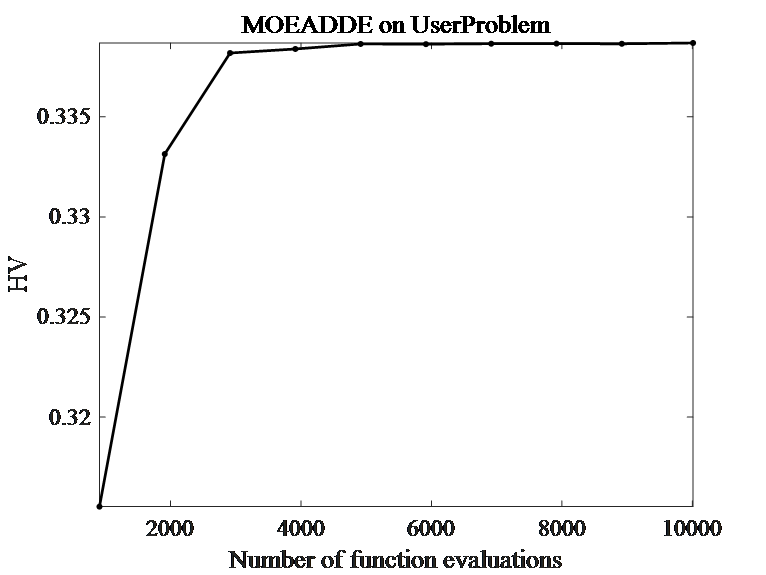
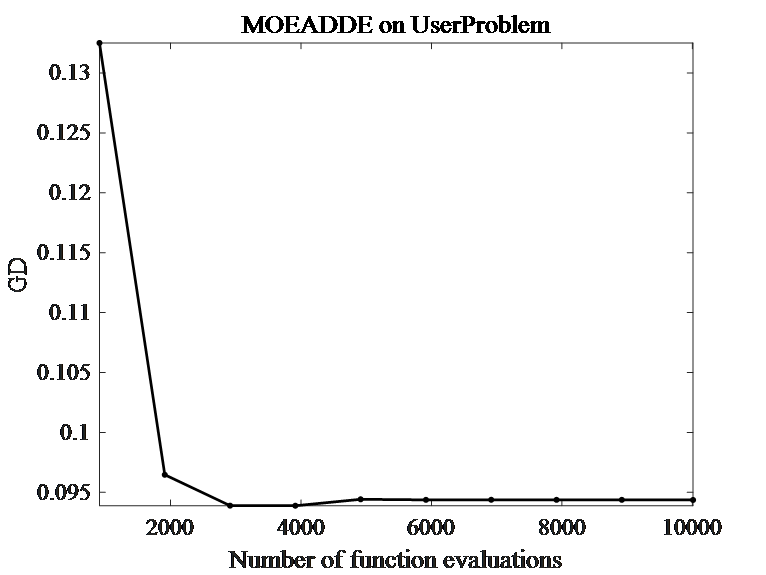
5.运行结果分析






![民航电子数据库:[E14024]事务内变更操作次数超过最大许可值10000,可通过系统参数max_trans_modify适当调整限制](https://img-blog.csdnimg.cn/direct/bf0860dc511c428ea02b5b76e388ad9b.jpeg)