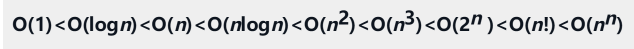3105. 最长的严格递增或递减子数组
题目
给你一个整数数组 nums 。
返回数组 nums 中 严格递增 或 严格递减 的最长非空子数组的长度。
思考:
返回什么:返回最长非空子数组的长度。return max(decs_len,incs_len);
但实际上我们只需要用一个变量ans就可以,不用使用decs_len,incs_len。如ans=(ans,cur_len);cur_len=right-left+1(这个是否要+1可以让left=right=0时判断)
方法一:暴力破解:
class Solution {
public:
int longestMonotonicSubarray(vector<int>& nums) {
int n = nums.size();
int ans = 1;
for (int i = 0; i < n; i++) {
for (int j = i+1;j < n; j++) {
if(nums[j]<=nums[j-1]){//不严格递增
break;
}//[i,j]严格递增
ans=max(j-i+1,ans);
}
for (int k= i+1; k< n; k++) {
if(nums[k]>=nums[k-1]){//不严格递减
break;
}
ans=max(k-i+1,ans);
}
}
return ans;
}
};
时间复杂度0(n²)
方法二:分组循环:
如例子nums = [1,2,3,4,3,3,2] ;
- 1.如果我们确定 【1,2,3,4】为递增数列,那么我们可以确定 【2,3,4】、【3,4】、【4】均为递增数列。 即开始点为left,结束点为right时,我们可以确定right-left+1个递增数列(3-0+1=4)
- 但需要注意,实际上我们结束点是第一个不满足的点,所以数量为right-left。
- 2.如果我们确定【1,2,3,4,3】不是递增数列,那我们要再从那个节点开始遍历呢?
- * 第一想法从 3开始遍历 即直接从上一个right++完之后遍历。但是捏,【4,3】不是递增数列说明什么说明,说明他是递减数列,所以我们要从4开始遍历,我们上一个right++(此时到3)完之后-1再遍历。
- 3.那我们怎么判断递增还是递减呢?可以用一个bool类型的变量 inc(1=增,0=减)
整体流程:
用right指针 遍历数组,如果连续两个元素重复,right后移,跳出循环,(再来一次判断)直到不相等。用left记录每次的起始点,right记录每次的结束点。如果数组严格单调且right不越界,right++。一次遍历之后更新ans,right从第一个不满足的点变为上一个节点
代码如下:
class Solution {
public:
int longestMonotonicSubarray(vector<int>& nums) {
int n = nums.size();
int ans = 1; // 初始化结果为1,因为最短的单调子数组长度至少为1
int left = 0; // 左边界初始位置
int right = 0; // 右边界初始位置
while (right < n - 1) { // 遍历数组,注意右边界不超过数组末尾的前一个元素
if (nums[right] == nums[right + 1]){
right++;
continue;
} // 如果右边界和下一个元素相同,继续向右移动右边界
left = right; // 更新左边界为当前右边界位置,记录这一组的开始位置
bool inc = nums[right + 1] - nums[right] > 0; // 判断单调性
right++; // 移动右边界到下一个位置
while (right < n && (nums[right] - nums[right - 1] > 0) == inc&&nums[right] != nums[right - 1] ) // 向右移动右边界直到不满足单调性为止
right++;
ans = max(ans, right - left); // 更新结果,当前子数组长度为右边界减去左边界
right-=1;
}
return ans;
}
};
时间复杂度:O(n)。时间复杂度乍一看是 O(n^2),但注意变量 i 减少的次数是 O(n)其它情况一直在增加,由于 i最大是 n,所以增加的次数是 O(n)所以二重循环总共循环 O(n) 次,时间复杂度是 O(n) 的。
空间复杂度:O(1)。仅用到若干额外变量。
分组循环使用条件: 如果按照题意,可以把数组分成若干段满足要求的子数组,每一段之间没有交集。
3106. 满足距离约束且字典序最小的字符串
题目
给你一个字符串 s 和一个整数 k 。
定义函数 distance(s1, s2) ,用于衡量两个长度为 n 的字符串 s1 和 s2 之间的距离,即:
字符 ‘a’ 到 ‘z’ 按 循环 顺序排列,对于区间 [0, n - 1] 中的 i ,计算所有【 s1[i] 和 s2[i] 之间 最小距离】的 和 。
例如,distance(“ab”, “cd”) = 4 ,且 distance(“a”, “z”) = 1 。
你可以对字符串 s 执行 任意次 操作。在每次操作中,可以将 s 中的一个字母 改变 为 任意 其他小写英文字母。
返回一个字符串,表示在执行一些操作后你可以得到的 字典序最小 的字符串 t ,且满足 distance(s, t) <= k
思路
- distance(“a”, “z”) = 1 这是因为字符 ‘a’ 到 ‘z’ 按 循环 顺序排列,Z的后面就是A。
所以距离distance_a(从当前元素x到a的距离)=min(x-‘a’,‘z’-x+1); - 要认清一个问题 a<b;abc<bbc;即越前面的元素越靠近a字典序越小
- 使用贪心算法,在k次内尽可能多的让元素变为a;当k不够变成A的时候,让元素直接-k变小即可。
代码:
class Solution {
public:
string getSmallestString(string s, int k) {
int n=s.size();
int i=0;
while(k>=0){
if(i==n) break;
char x=s[i];
int dis=min(x-'a','z'-x+1);
if(k>=dis){
s[i++]='a';
k-=dis;
}
else{
s[i++]-=k;
break;
}
}
return s;
}
};
时间复杂度:O(n),空间复杂度:O(1), C++ 可以原地修改字符串。
class Solution:
def getSmallestString(self, s: str, k: int) -> str:
s=list(s)
for i,x in enumerate(map(ord,s)):
dis=min(x-ord('a'),ord('z')-x+1)
if k>=dis:
s[i]='a'
k-=dis
else:
s[i]=chr(x-k)
break
return''.join(s)
字符串转换为了列表 s,这会占用额外的空间。在 Python 中,字符串是不可变的,因此将其转换为列表以便修改会增加空间复杂度。将其转换为列表需要额外的 O(n) 空间。
时间复杂度:O(n),空间复杂度:O(n)
3107. 使数组中位数等于 K 的最少操作数
题目
给你一个整数数组 nums 和一个非负整数 k 。一次操作中,你可以选择任一元素 加 1 或者减 1 。
请你返回将 nums 中位数 变为 k 所需要的 最少 操作次数。
一个数组的中位数指的是数组按非递减顺序排序后最中间的元素。如果数组长度为偶数,我们选择中间两个数的较大值为中位数。
示例
示例 1:
输入:nums = [2,5,6,8,5], k = 4
输出:2
解释:我们将 nums[1] 和 nums[4] 减 1 得到 [2, 4, 6, 8, 4] 。现在数组的中位数等于 k 。
示例 2:
输入:nums = [2,5,6,8,5], k = 7
输出:3
解释:我们将 nums[1] 增加 1 两次,并且将 nums[2] 增加 1 一次,得到 [2, 7, 7, 8, 5] 。
思考
- 这道题的中位数是什么,定义方式–》看加粗字体。由此我们能得出来,中位数的下标为n/2(数组排序后);例如:【0,1,2】中位数下表为3/2=1;【0,1,2,3】中位数下表为4/2=2.(中间较大的那个)。
- 示例一:nums = [2,5,6,8,5]–》sort后为 [2,5,5,6,8] 那么我们怎么让中位数=4呢?其实不难想到需要先将中间的数X变为4,但是这样子数组【5,4】还得再次变换?不用那么麻烦,直接将【5,4】中的5也变成4即可。如此就有数组[2,4,4,6,8] 中位数为4(而在此期间,6,8我们没有进行处理这是因为中间的数X>4,那么排序后 后面的数也必然大于4,不用进行操作。);示例二同样。
- 经过示例一二:我们可以得出结论:我们只需要将数组排序,然后让中间的数X变为k,再将X的前小于或后大于的数进行变动。
代码
class Solution {
public:
long long minOperationsToMakeMedianK(vector<int>& nums, int k) {
long long ans = 0;//切记设置成龙龙
sort(nums.begin(), nums.end());
long long mid = nums.size() / 2;
if (nums[mid] == k)
return 0;
if (nums[mid] > k) {
for (long long i = mid; i >= 0; i--) {//切记i==0!!!
if (nums[i] > k)
ans += nums[i] - k;
else
break;//一个小于前面的都小
}
} // 前面的可能也大于
if (nums[mid] < k) {
for (long long i = mid; i < nums.size(); i++) {
if (nums[i] < k)
ans += k - nums[i];
else
break;
}
}
return ans;
}
};
3108. 带权图里旅途的最小代价
题目
给你一个 n 个节点的带权无向图,节点编号为 0 到 n - 1 。
给你一个整数 n 和一个数组 edges ,其中 edges[i] = [ui, vi, wi] 表示节点 ui 和 vi 之间有一条权值为 wi 的无向边。
在图中,一趟旅途包含一系列节点和边。旅途开始和结束点都是图中的节点,且图中存在连接旅途中相邻节点的边。注意,一趟旅途可能访问同一条边或者同一个节点多次。
如果旅开始于节点 u ,结束于节点 v ,我们定义这一趟旅途的 代价 是经过的边权按位与 AND 的结果。换句话说,如果经过的边对应的边权为 w0, w1, w2, …, wk ,那么代价为w0 & w1 & w2 & … & wk ,其中 & 表示按位与 AND 操作。
给你一个二维数组 query ,其中 query[i] = [si, ti] 。对于每一个查询,你需要找出从节点开始 si ,在节点 ti 处结束的旅途的最小代价。如果不存在这样的旅途,答案为 -1 。
返回数组 answer ,其中 answer[i] 表示对于查询 i 的 最小 旅途代价。
示例
示例 1:
输入:n = 5, edges = [[0,1,7],[1,3,7],[1,2,1]], query = [[0,3],[3,4]]
输出:[1,-1]
解释:

第一个查询想要得到代价为 1 的旅途,我们依次访问:0->1(边权为 7 )1->2 (边权为 1 )2->1(边权为 1 )1->3 (边权为 7 )。
第二个查询中,无法从节点 3 到节点 4 ,所以答案为 -1 。
思路:
- 按位与 AND:按位与操作:1&1=0,1&0=0;0&0=0;他有一条性质是数 越与越小。
例如示例一:7=111 1=001 7&1=111&001=001;
=按位与运算的初始值可以用-1 原因:-1的补码是1111111。 - 本题可以分为三大类情况:(起始点记为start,结束点记为finish)
1. start==finish,路径代价为0
2. start,finish 两个点不联通 路径代价为-1
3. start,finish 两个点联通 ,路径代价为 当前图的所有路径相与值。 - 如此,大体思路即为,建立两个数组。一个数组存放当前点所在图的编号;另一个数组cc_and存放当前图的所有路径相与值,结合三种情况,求出最终结果。
代码:
class Solution {
vector<vector<pair<int, int>>> g;
vector<int> cc_and, ids;
int dfs(int x) {
ids[x] = cc_and.size(); // 记录每个点所在连通块的编号
int and_ = -1;
for (auto &[y, w]: g[x]) {
and_ &= w;
if (ids[y] < 0) { // 没有访问过
and_ &= dfs(y);
}
}
return and_;
}
public:
vector<int> minimumCost(int n, vector<vector<int>> &edges, vector<vector<int>> &query) {
g.resize(n);
for (auto &e: edges) {
int x = e[0], y = e[1], w = e[2];
g[x].emplace_back(y, w);
g[y].emplace_back(x, w);
}
ids.resize(n, -1); // 记录每个点所在连通块的编号
for (int i = 0; i < n; i++) {
if (ids[i] < 0) { // 没有访问过
cc_and.push_back(dfs(i)); // 记录每个连通块的边权的 AND
}
}
vector<int> ans;
ans.reserve(query.size()); // 预分配空间
for (auto &q: query) {
int s = q[0], t = q[1];
ans.push_back(ids[s] != ids[t] ? -1 : cc_and[ids[s]]);
}
return ans;
}
};
时间复杂度:O(n+m+q) 的长度。
空间复杂度:O(n+m)。返回值不计入。
以上over 。


![民航电子数据库:[E14024]事务内变更操作次数超过最大许可值10000,可通过系统参数max_trans_modify适当调整限制](https://img-blog.csdnimg.cn/direct/bf0860dc511c428ea02b5b76e388ad9b.jpeg)