文章目录
- 二重积分的基本概念
- 二重积分的性质
- 累次积分
- 计算二重积分的方法和技巧
- 描点画图法
- 对称性
- 利用函数的奇偶性
- 变量的轮换对称性
- 积分次序的选择
- 积分区域的确认
- 先看变量和先积变量
- 基本原则
- 穿线法确定先积变量的曲线范围
- 常见的曲线
- 经典题目
二重积分的基本概念
定义:设函数
z
=
f
(
x
,
y
)
z=f(x,y)
z=f(x,y)在有界区域
D
D
D上有定义,将区域
D
D
D任意分成
n
n
n个小区域
Δ
σ
1
,
Δ
σ
2
,
.
.
.
,
Δ
σ
n
\Delta\sigma_1,\Delta\sigma_2,...,\Delta\sigma_n
Δσ1,Δσ2,...,Δσn其中
Δ
σ
i
\Delta\sigma_i
Δσi代表第
i
i
i个小区域,也表示它的面积,在每个
Δ
σ
i
\Delta\sigma_i
Δσi上任取一点
(
ξ
i
,
η
i
)
(\xi_i,\eta_i)
(ξi,ηi),做乘积
f
(
ξ
i
,
η
i
)
Δ
σ
i
f(\xi_i,\eta_i)\Delta\sigma_i
f(ξi,ηi)Δσi,并求和
∑
i
=
1
n
f
(
ξ
i
,
η
i
)
Δ
σ
i
\sum_{i=1}^nf(\xi_i,\eta_i)\Delta\sigma_i
i=1∑nf(ξi,ηi)Δσi记
λ
\lambda
λ为
n
n
n个小区中的最大 直径,如果
lim
λ
→
0
∑
i
=
1
n
f
(
ξ
i
,
η
i
)
Δ
σ
i
\lim\limits_{\lambda\to0}\sum_{i=1}^nf(\xi_i,\eta_i)\Delta\sigma_i
λ→0limi=1∑nf(ξi,ηi)Δσi存在,则称
f
(
x
,
y
)
f(x,y)
f(x,y)在区域
D
D
D上的二重积分,记为
∬
D
f
(
x
,
y
)
d
σ
=
lim
λ
→
0
∑
i
=
1
n
f
(
ξ
i
,
η
i
)
Δ
σ
i
\underset{D}{\iint}f(x,y)d\sigma=\lim\limits_{\lambda\to 0}\sum_{i=1}^nf(\xi_i,\eta_i)\Delta\sigma_i
D∬f(x,y)dσ=λ→0limi=1∑nf(ξi,ηi)Δσi
几何意义:二重积分
∬
D
f
(
x
,
y
)
d
σ
\underset{D}{\iint}f(x,y)d\sigma
D∬f(x,y)dσ是一个数:
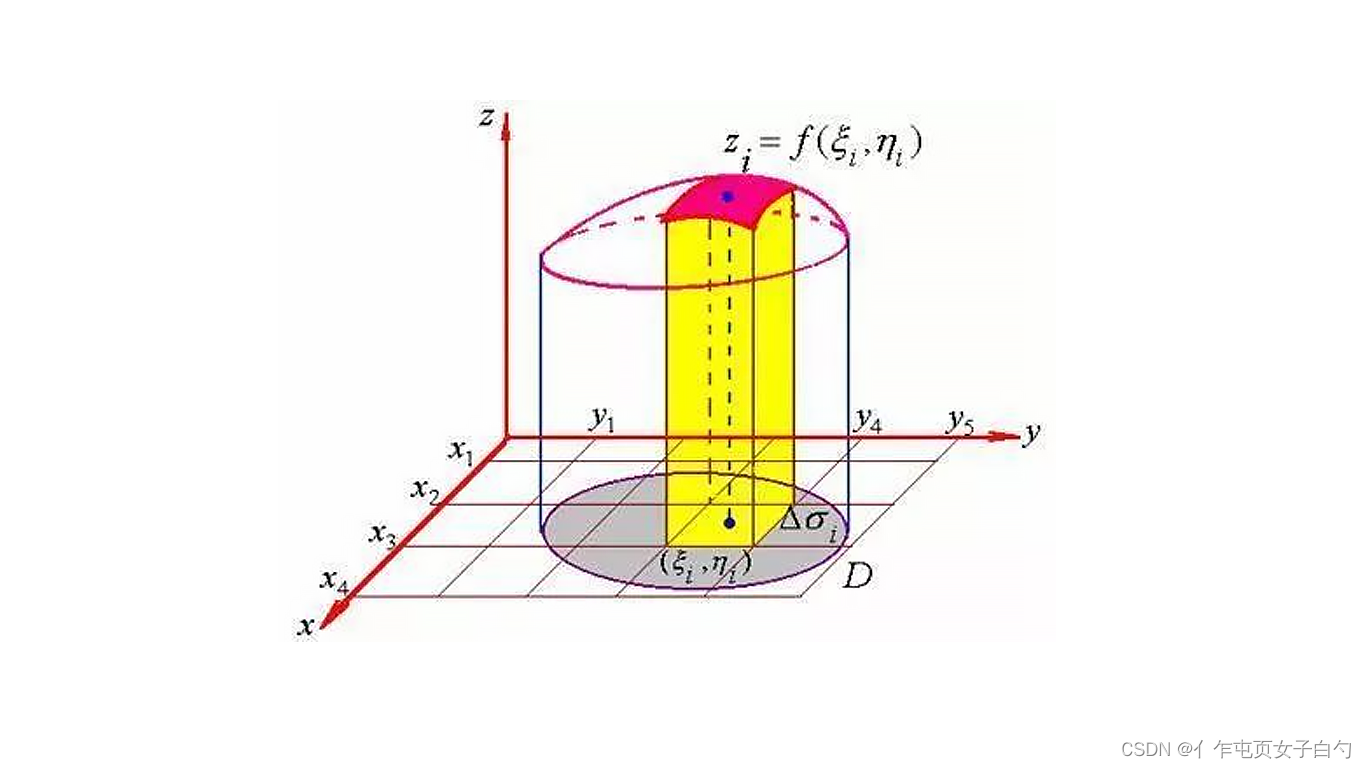
- 当 f ( x , y ) ≥ 0 f(x,y)≥0 f(x,y)≥0时,其值等于以区域 D D D为底,以曲面 z = f ( x , y ) z=f(x,y) z=f(x,y)为顶的曲顶柱体的体积。
- 当 f ( x , y ) ≤ 0 f(x,y)≤0 f(x,y)≤0时,二重积分的值为负数,其绝对值等于以区域 D D D为底,以曲面 z = f ( x , y ) z=f(x,y) z=f(x,y)为顶的曲顶柱体的体积。
二重积分的性质
- ∬ D f ( x , y ) + g ( x , y ) d σ = ∬ D f ( x , y ) d σ + ∬ D D g ( x , y ) d σ \underset{D}{\iint}f(x,y)+g(x,y)d\sigma=\underset{D}{\iint}f(x,y)d\sigma+\underset{D}{\iint}Dg(x,y)d\sigma D∬f(x,y)+g(x,y)dσ=D∬f(x,y)dσ+D∬Dg(x,y)dσ
- ∬ D k f ( x , y ) d σ = k ∬ D f ( x , y ) d σ \underset{D}{\iint}kf(x,y)d\sigma=k\underset{D}{\iint}f(x,y)d\sigma D∬kf(x,y)dσ=kD∬f(x,y)dσ
- 若区域 D D D上 f ( x , y ) = k f(x,y)=k f(x,y)=k, σ \sigma σ为区域 D D D的面积,则: ∬ D f ( x , y ) d σ = ∬ D k d σ = k ∬ D 1 d σ = k σ \underset{D}{\iint}f(x,y)d\sigma=\underset{D}{\iint}kd\sigma=k\underset{D}{\iint}1d\sigma=k\sigma D∬f(x,y)dσ=D∬kdσ=kD∬1dσ=kσ
- 不等式性质:
- 若在区域 D D D上 f ( x , y ) ≤ g ( x , y ) f(x,y)≤g(x,y) f(x,y)≤g(x,y),则 ∬ D f ( x , y ) d σ ≤ ∬ D g ( x , y ) d σ \underset{D}{\iint}f(x,y)d\sigma≤\underset{D}{\iint}g(x,y)d\sigma D∬f(x,y)dσ≤D∬g(x,y)dσ
- 若在区域 D D D上 m ≤ f ( x , y ) ≤ M m≤f(x,y)≤M m≤f(x,y)≤M,则 m σ ≤ ∬ D f ( x , y ) d σ ≤ M σ m\sigma≤\underset{D}{\iint}f(x,y)d\sigma≤M\sigma mσ≤D∬f(x,y)dσ≤Mσ其中 σ \sigma σ为区域 D D D的面积。
- ∣ ∬ D f ( x , y ) d σ ∣ ≤ ∬ D ∣ f ( x , y ) ∣ d σ |\underset{D}{\iint}f(x,y)d\sigma|≤\underset{D}{\iint}|f(x,y)|d\sigma ∣D∬f(x,y)dσ∣≤D∬∣f(x,y)∣dσ
- 中值定理:设函数 f ( x , y ) f(x,y) f(x,y)在闭区域 D D D上连续, σ \sigma σ为区域 D D D的面积,则在 D D D上至少存在一点 ( ξ , η ) (\xi,\eta) (ξ,η),使得 ∬ D f ( x , y ) d σ = f ( ξ , η ) σ \underset{D}{\iint}f(x,y)d\sigma=f(\xi,\eta)\sigma D∬f(x,y)dσ=f(ξ,η)σ
累次积分
设
f
(
x
,
y
)
f(x,y)
f(x,y)在区域
D
:
a
≤
x
≤
b
,
c
≤
y
≤
d
D:a\leq x\leq b,c\leq y\leq d
D:a≤x≤b,c≤y≤d上可积,其积分值与分割方法无关,那么可选用平行于坐标轴的两组直线来分割
D
D
D,则对区间
[
a
,
b
]
[a,b]
[a,b]中的任一点
x
x
x积分(一条垂直于
x
x
x轴的线):
F
(
x
)
=
∫
c
d
f
(
x
,
y
)
d
y
F(x)=\int^d_cf(x,y)dy
F(x)=∫cdf(x,y)dy
存在,
F
(
x
)
F(x)
F(x)也是
[
a
,
b
]
[a,b]
[a,b]上
x
x
x的可积函数,并且积分
∫
a
b
F
(
x
)
d
x
\int_a^bF(x)dx
∫abF(x)dx
也存在,因此二重积分可用累次积分进行积分,即
∬
D
f
(
x
,
y
)
d
σ
=
∫
a
b
d
x
∫
c
d
f
(
x
,
y
)
d
y
\underset{D}{\iint}f(x,y)d\sigma=\int_a^bdx\int_c^df(x,y)dy
D∬f(x,y)dσ=∫abdx∫cdf(x,y)dy
同样的,也可以先对
x
x
x后对
y
y
y积分:
∬
D
f
(
x
,
y
)
d
σ
=
∫
c
d
d
y
∫
a
b
f
(
x
,
y
)
d
x
\underset{D}{\iint}f(x,y)d\sigma=\int_c^ddy\int_a^bf(x,y)dx
D∬f(x,y)dσ=∫cddy∫abf(x,y)dx
有许多二重积分仅仅依靠直角坐标下化为累次积分的方法难以达到简化和求解的目的。当积分区域为圆域,环域,扇域等,或被积函数为
f
(
x
2
+
y
2
)
,
f
(
y
x
)
,
f
(
x
y
)
f(\sqrt{x^2+y^2}),f(\frac{y}{x}),f(\frac{x}{y})
f(x2+y2),f(xy),f(yx)等形式时,采用极坐标会方便。在直角坐标系
x
O
y
xOy
xOy中,取原点为极坐标的极点,取正
x
x
x轴为极轴,则点
P
P
P的直角坐标系
(
x
,
y
)
(x,y)
(x,y)与极坐标轴
(
r
,
θ
)
(r,\theta)
(r,θ)之间有关系式:
- x = r c o s θ x=rcos\theta x=rcosθ
- y = r s i n θ y=rsin\theta y=rsinθ
- x 2 + y 2 = r 2 x^2+y^2=r^2 x2+y2=r2
- t a n θ = y x tan\theta=\frac{y}{x} tanθ=xy
为得到极坐标下的面积元素
d
σ
dσ
dσ的转换,用坐标曲线网去分割
D
D
D,即用
O
O
O为圆心
r
r
r为半径的圆和
O
O
O为起点的射线去无穷分割
D
D
D。仿照直角坐标系下面积元素的取法,在
(
r
,
θ
)
(r,\theta)
(r,θ)处取一个圆心角为
d
θ
d\theta
dθ,宽度为
d
r
dr
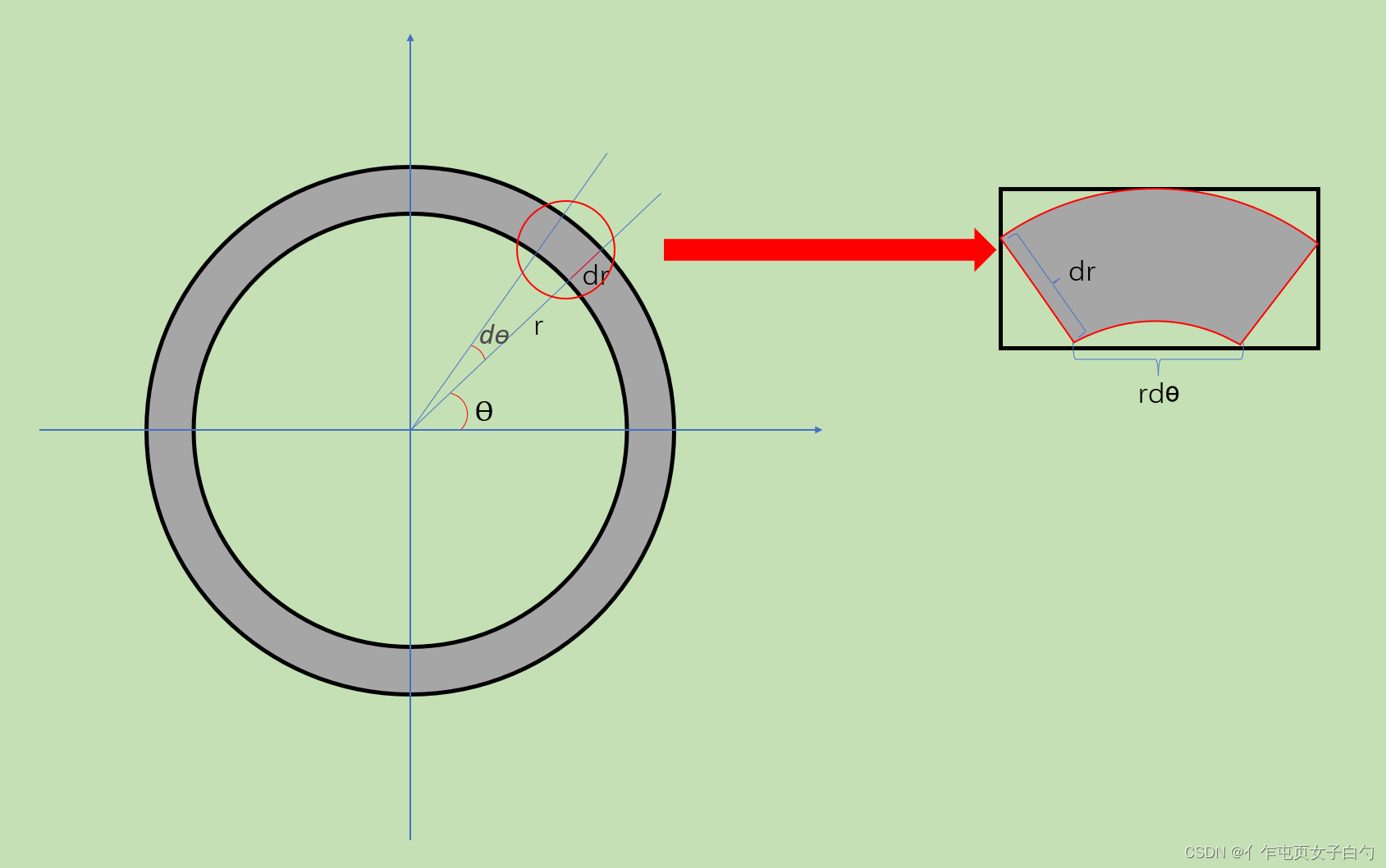
dr 的小扇环作为面积元素。为了方便计算,我们不妨把这个小扇环看作一个矩形,,那么它的长宽分别为
r
d
θ
rd\theta
rdθ(弧长)和
d
r
dr
dr ,那么
d
σ
=
r
d
θ
r
d
dσ=rd\theta rd
dσ=rdθrd
同样的,对于极坐标也有两种积分次序:
- 先 r r r后 θ \theta θ:
∬ D f ( x , y ) d σ = ∫ α β d θ ∫ φ ( α ) φ ( β ) f ( r c o s θ , r s i n θ ) r d r \underset{D}{\iint}f(x,y)d\sigma=\int_\alpha^\beta d\theta\int_{\varphi(\alpha)}^{\varphi(\beta)}f(rcos\theta,rsin\theta)rdr D∬f(x,y)dσ=∫αβdθ∫φ(α)φ(β)f(rcosθ,rsinθ)rdr
- 先
θ
\theta
θ后
r
r
r:
∬ D f ( x , y ) d σ = ∫ a b d r ∫ φ ( a ) φ ( b ) f ( r c o s θ , r s i n θ ) r d θ \underset{D}{\iint}f(x,y)d\sigma=\int_a^bdr\int_{\varphi(a)}^{\varphi(b)}f(rcos\theta,rsin\theta)rd\theta D∬f(x,y)dσ=∫abdr∫φ(a)φ(b)f(rcosθ,rsinθ)rdθ
最后,若区域
D
D
D上
f
(
x
,
y
)
=
g
(
x
)
h
(
y
)
f(x,y)=g(x)h(y)
f(x,y)=g(x)h(y),则:
∬
D
f
(
x
,
y
)
d
σ
=
∫
g
(
x
)
d
x
∫
h
(
y
)
d
y
\underset{D}{\iint}f(x,y)d\sigma=\int g(x)dx\int h(y)dy
D∬f(x,y)dσ=∫g(x)dx∫h(y)dy
极坐标也同样适用。
计算二重积分的方法和技巧
二重积分的计算应该严格按照以下步骤进行:
- 画图
- 观察对称性
- 选择坐标系,选择积分次序
- 化为累次积分并计算
描点画图法
有时题目中的积分区域会由一个复杂的参数方程或极坐标方程确定,比如
{
x
=
c
o
s
3
t
y
=
s
i
n
3
t
①
\tag*① \begin{cases} x=cos^3t\\ y=sin^3t \end{cases}
{x=cos3ty=sin3t①
对于这种函数如果想先将其转为直角坐标方程再画图是十分困难的,此时就应该使用描点画图法,描点画图法的思想为:
- 确定函数的增减区域,把增减区域的端点列表后,描点画图。
对于①来说,其中 x x x的单调分界点为 t = 0 , π , 2 π , … t=0,\pi,2\pi,\dots t=0,π,2π,…; y y y的单调分界点为 t = − π 2 , π 2 , 3 π 2 , … t=-\frac{\pi}{2},\frac{\pi}{2},\frac{3\pi}{2},\dots t=−2π,2π,23π,…。那么可做表如下:
| t t t | 0 0 0 | ( 0. π 2 ) (0.\frac{\pi}{2}) (0.2π) | π 2 \frac{\pi}{2} 2π | ( π 2 , π ) (\frac{\pi}{2},\pi) (2π,π) | π \pi π | ( π , 3 π 2 ) (\pi,\frac{3\pi}{2}) (π,23π) | 3 π 2 \frac{3\pi}{2} 23π | ( 3 π 2 , 2 π ) (\frac{3\pi}{2},2\pi) (23π,2π) | 2 π 2\pi 2π | ( 2 π , 5 π 2 ) (2\pi,\frac{5\pi}{2}) (2π,25π) |
|---|---|---|---|---|---|---|---|---|---|---|
| x = c o s 3 t x=cos^3t x=cos3t | 1 | ↘ | 0 | ↘ | -1 | ↗ | 0 | ↗ | 1 | 重复 |
| y = s i n 3 t y=sin^3t y=sin3t | 0 | ↗ | 1 | ↘ | 0 | ↘ | -1 | ↗ | 0 | 重复 |
由此可作图得:
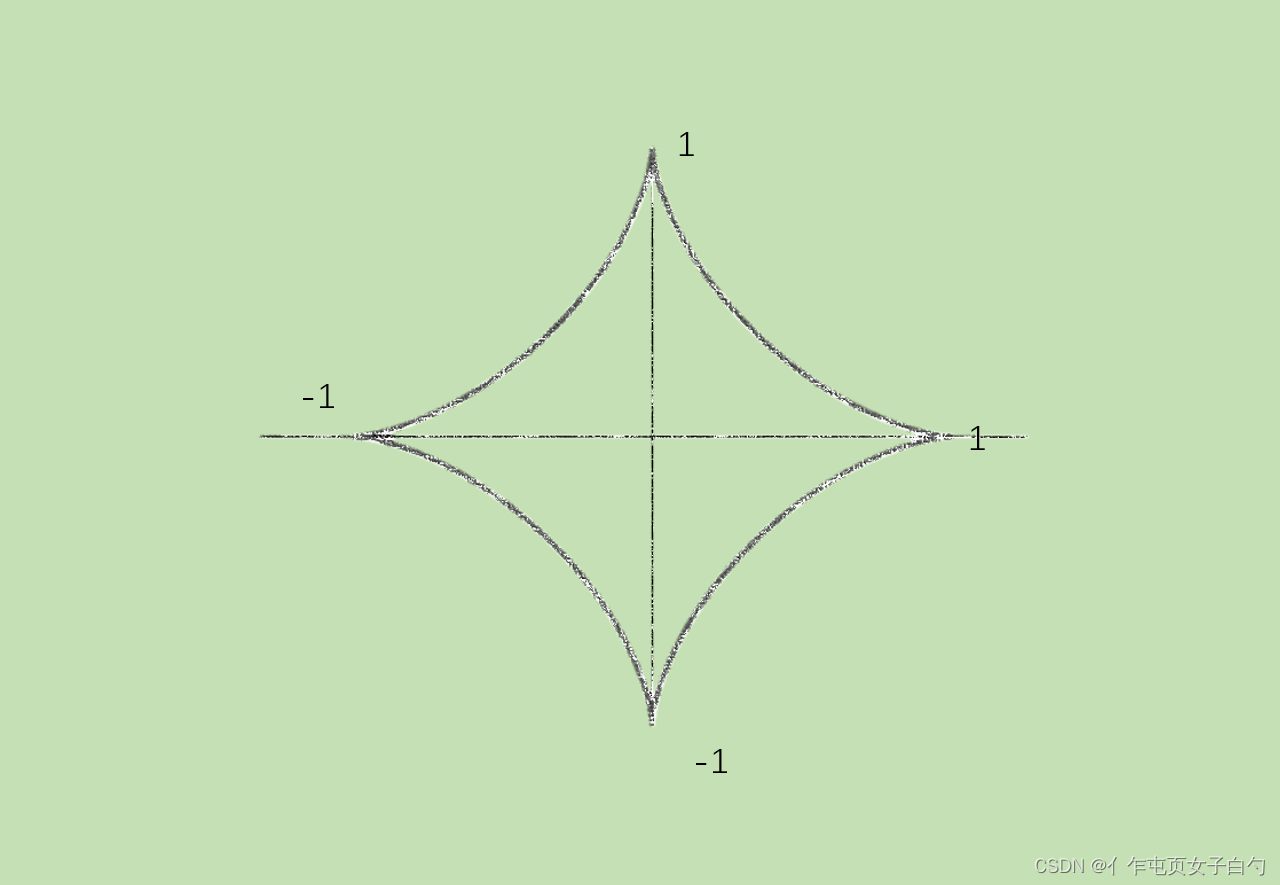
考研常考的曲线见下文常见曲线。
对称性
利用函数的奇偶性
- 若积分区域 D D D关于 y y y轴对称, f ( x , y ) f(x,y) f(x,y)关于 x x x轴有奇偶性,则 ∬ D f ( x , y ) d σ = { 2 ∬ D x ≥ 0 f ( x , y ) d σ , f ( x , y ) 关于 x 为偶函数 0 , f ( x , y ) 关于 x 为奇函数 \underset{D}{\iint}f(x,y)d\sigma=\begin{cases}2\underset{D_x≥0}{\iint}f(x,y)d\sigma,f(x,y)关于x为偶函数\\0,f(x,y)关于x为奇函数\end{cases} D∬f(x,y)dσ=⎩ ⎨ ⎧2Dx≥0∬f(x,y)dσ,f(x,y)关于x为偶函数0,f(x,y)关于x为奇函数
- 若积分区域 D D D关于 x x x轴对称, f ( x , y ) f(x,y) f(x,y)关于 y y y轴有奇偶性,则 ∬ D f ( x , y ) d σ = { 2 ∬ D y ≥ 0 f ( x , y ) d σ , f ( x , y ) 关于 y 为偶函数 0 , f ( x , y ) 关于 y 为奇函数 \underset{D}{\iint}f(x,y)d\sigma=\begin{cases}2\underset{D_y≥0}{\iint}f(x,y)d\sigma,f(x,y)关于y为偶函数\\0,f(x,y)关于y为奇函数\end{cases} D∬f(x,y)dσ=⎩ ⎨ ⎧2Dy≥0∬f(x,y)dσ,f(x,y)关于y为偶函数0,f(x,y)关于y为奇函数
变量的轮换对称性
如果积分区域 D D D具有轮换对称性,也就是关于直线 y = x y=x y=x对称,即 D D D的表达式中将 x x x换作 y y y, y y y换作 x x x表达式不变,则 ∬ D f ( x , y ) d σ = ∬ D f ( y , x ) d σ = 1 2 ∬ D f ( x , y ) + f ( y , x ) d x d y \underset{D}{\iint}f(x,y)d\sigma=\underset{D}{\iint}f(y,x)d\sigma=\frac{1}{2}\underset{D}{\iint}f(x,y)+f(y,x)dxdy D∬f(x,y)dσ=D∬f(y,x)dσ=21D∬f(x,y)+f(y,x)dxdy
积分次序的选择
积分次序的选择是指在将二重积分化为累次积分时先对哪个自变量进行积分,并且有一类题就是要求转换积分次序:
- 在直角坐标系下选择的标准为:根据被积函数对哪个自变量的积分难易程度决定。
- 如果被积函数对 x x x好积,那么就先对 y y y积分;
- 如果被积函数对 y y y好积,那么就先对 x x x积分;
- 在极坐标下:绝大多数情况下先对 θ \theta θ再对 r r r
积分区域的确认
确定好积分次序后就需要确认每个自变量的积分区域。
先看变量和先积变量
上文我们提到,若
f
(
x
,
y
)
f(x,y)
f(x,y)在区域
D
:
a
≤
x
≤
b
,
c
≤
y
≤
d
D:a\leq x\leq b,c\leq y\leq d
D:a≤x≤b,c≤y≤d上可积,其积分值与分割方法无关,那么可选用平行于坐标轴的两组直线来分割
D
D
D,则对区间
[
a
,
b
]
[a,b]
[a,b]中的任一点
x
x
x积分(一条垂直于
x
x
x轴的线):
F
(
x
)
=
∫
c
d
f
(
x
,
y
)
d
y
F(x)=\int^d_cf(x,y)dy
F(x)=∫cdf(x,y)dy
存在,
F
(
x
)
F(x)
F(x)也是
[
a
,
b
]
[a,b]
[a,b]上
x
x
x的可积函数,并且积分
∫
a
b
F
(
x
)
d
x
\int_a^bF(x)dx
∫abF(x)dx
也存在,因此二重积分可用累次积分进行积分,即
∬
D
f
(
x
,
y
)
d
σ
=
∫
a
b
d
x
∫
c
d
f
(
x
,
y
)
d
y
\underset{D}{\iint}f(x,y)d\sigma=\int_a^bdx\int_c^df(x,y)dy
D∬f(x,y)dσ=∫abdx∫cdf(x,y)dy
在这个表述中:
- x x x是先看变量, y y y是后看变量。
- y y y是先积变量, x x x是后积变量。
基本原则
在直角坐标系下:
- 先看变量的范围是数值范围: [ 最小值,最大值 ] [最小值,最大值] [最小值,最大值];
- 先积变量的范围是曲线范围: [ 小的一侧曲线,大的一侧曲线 ] [小的一侧曲线,大的一侧曲线] [小的一侧曲线,大的一侧曲线];
- 若先积变量的某一侧曲线不能统一写为一个表达式,则对先看变量分段处理,然后再在每一段确定先积变量的曲线范围。
在极坐标下和再直角坐标系下基本一致区别在于:
- 先看角度的数值范围:从 0 0 0度逆时针到 2 π 2\pi 2π,来看从小到大;
- 先看极径的数值范围:从原点,到外侧圆环来看从小到大;
穿线法确定先积变量的曲线范围
先看变量的数值范围就是积分区域能取到的先看变量的最大值最小值,先积变量的曲线范围可以使用穿线法确定:
- 在直角坐标系下:
- 先积 x x x的曲线范围:把 y y y看作常数,即做一条垂直于 y y y轴穿过积分区域的直线,直线进入和离开的边界曲线即为 x x x的曲线范围。
- 先积 y y y的曲线范围:把 x x x看看作常数,即做一条垂直于 x x x轴穿过积分区域的直线,直线进入和离开的边界曲线即为 y y y的曲线范围。
- 在极坐标下:
- 先积极径的曲线范围: 把角度看作常数,即从极点引一条直线穿过积分区域,直线进入和离开的边界曲线即为极径的曲线范围。
- 先积角度的曲线范围:把极径看作常数,即以极点为圆心做圆穿过积分区域,圆进入和离开的边界曲线即为角度的曲线范围。
常见的曲线
所有考研可能出现的复杂的积分区域如下,最好根据方程用描点画图法画一下。图片出自同济大学高等数学第七版上册附录Ⅲ:

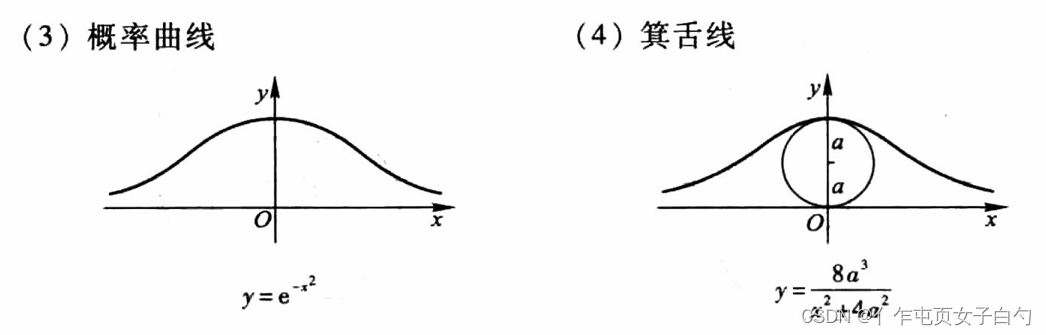
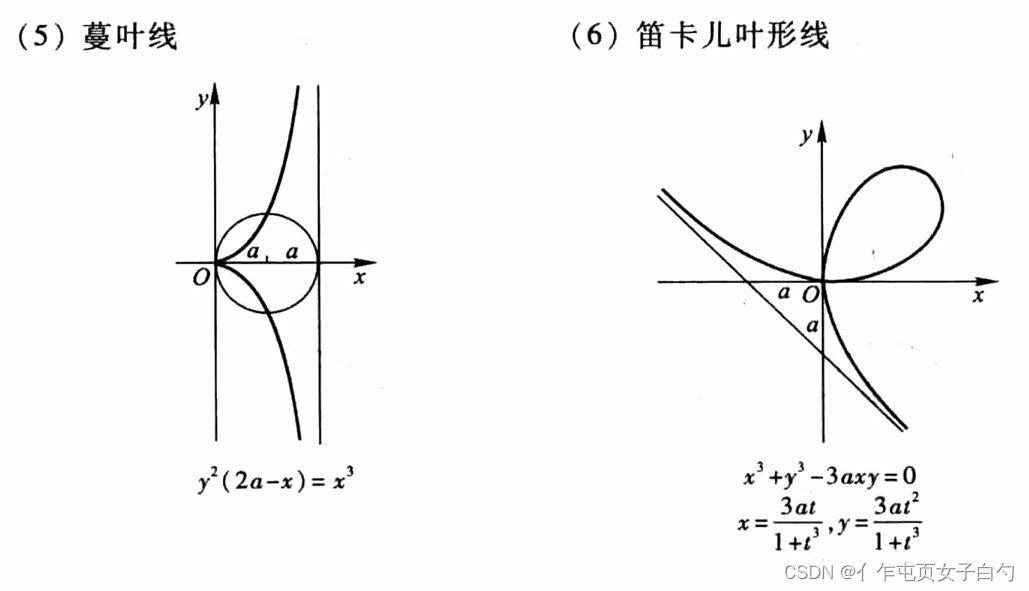
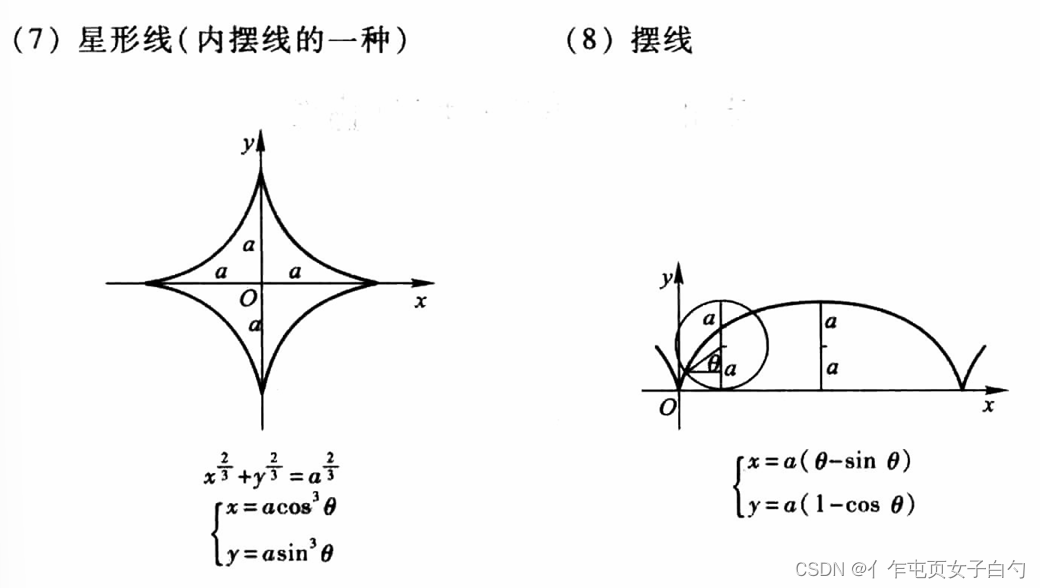

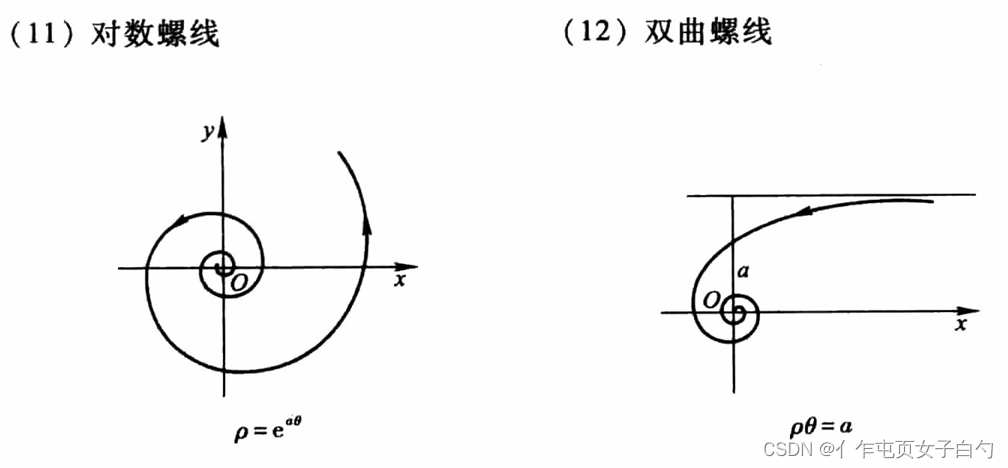
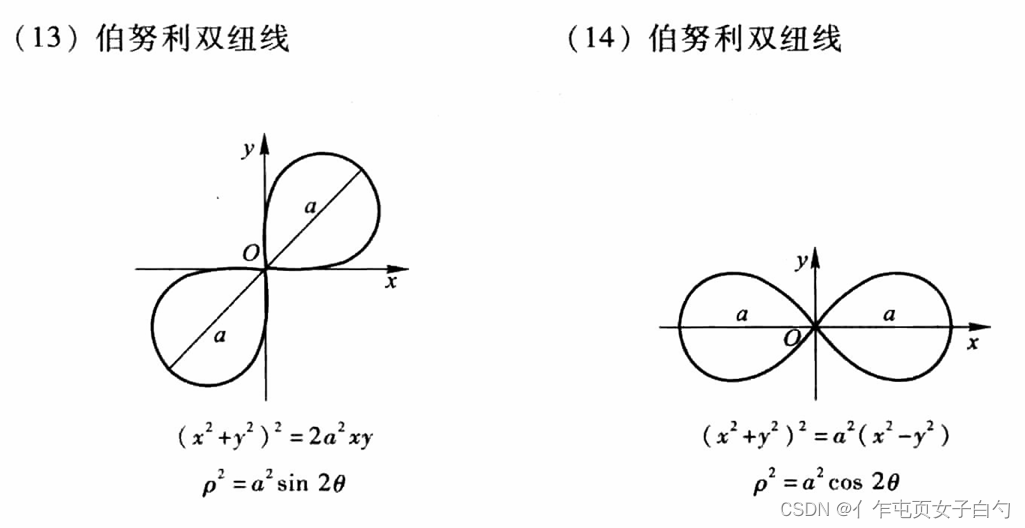
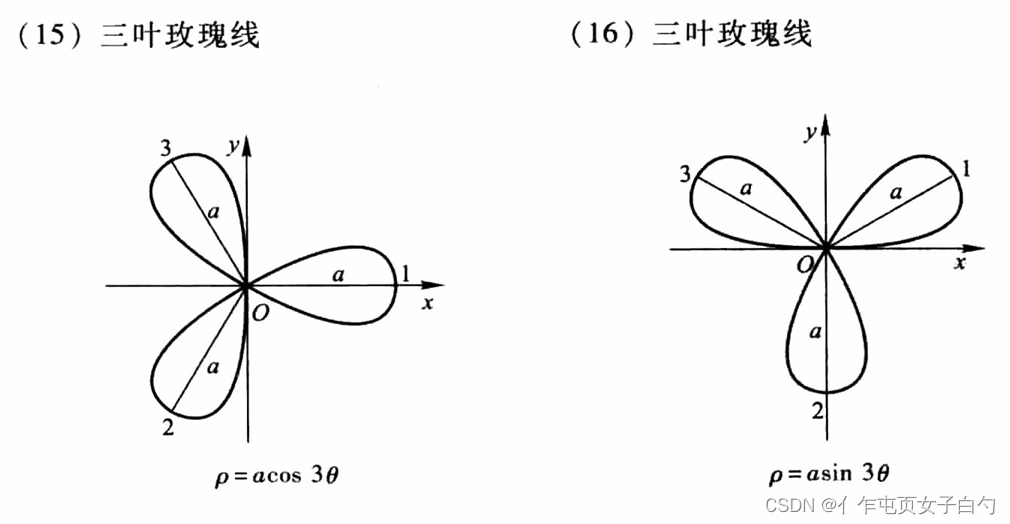
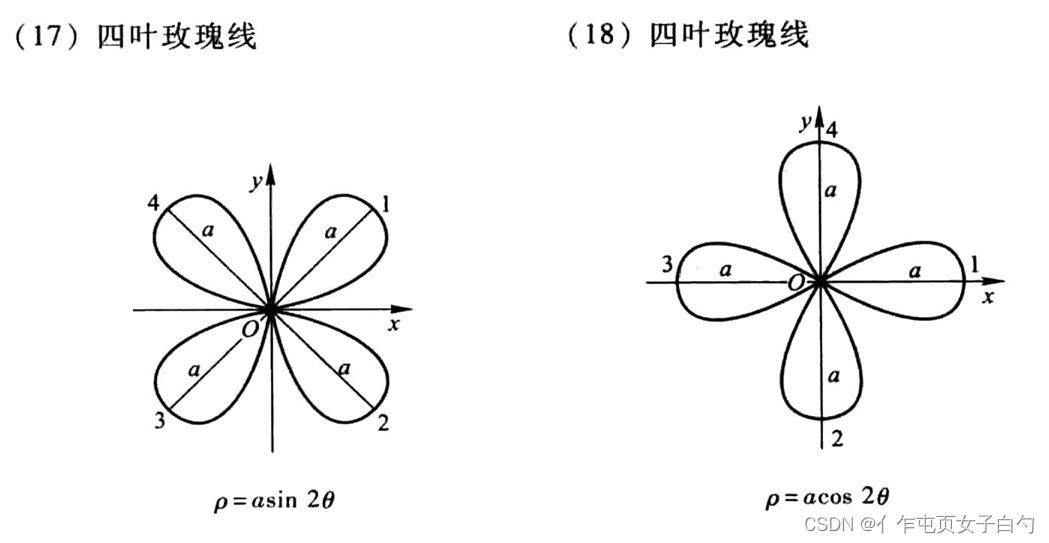
经典题目
不会的问我哦
- 定义类型:计算 lim n → ∞ ∑ i = 1 n ∑ j = 1 n 1 ( 1 + i n ) ( n 2 + j 2 ) \lim\limits_{n\to\infty}\sum_{i=1}^n\sum_{j=1}^n\frac{1}{(1+\frac{i}{n})(n^2+j^2)} n→∞limi=1∑nj=1∑n(1+ni)(n2+j2)1
- 复杂积分区域类型:计算 ∬ D y 2 d σ \underset{D}{\iint}y^2d\sigma D∬y2dσ其中 D D D由 { x = a ( t − s i n t ) y = a ( 1 − c o s t ) \begin{cases}x=a(t-sint)\\y=a(1-cost)\end{cases} {x=a(t−sint)y=a(1−cost) ( 0 ≤ t ≤ 2 π ) (0\leq t\leq2\pi) (0≤t≤2π),与 y = 0 y=0 y=0围成。
- 极坐标交换积分次序类型: I = ∫ − π 4 π 2 d θ ∫ 0 2 a c o s θ f ( r c o s θ , r s i n θ ) r d r I=\int_{-\frac{\pi}{4}}^{\frac{\pi}{2}}d\theta\int_0^{2acos\theta} f(rcos\theta,rsin\theta)rdr I=∫−4π2πdθ∫02acosθf(rcosθ,rsinθ)rdr