纯质数

题目：

思路：

一个最简单的思路就是枚举出所有的质数，然后再判断这个质数是否是一个纯质数。

1. 枚举出所有的质数：

   可以使用常规的暴力求解法，其时间复杂度为（$O(N\sqrt{N})$），而埃氏筛法的时间复杂度为($O(N\log \log n)$)，如果需要判断单个数是否为素数，试除法是更合适的选择；而如果需要求解一定范围内的素数，则埃拉托斯特尼筛法效率更高。这里我们使用埃氏筛法求解给定范围内的所有素数。

2. 判断纯质数：

   一个直接的思路是，遍历质数的每一位，判断该位置上的数是否为质数，因为对于每一位，如果是质数的话，那么这些数是固定的，即：2 3 5 7，我们可以将其写入到一个哈希表中，可以使用map库进行存储（map的查询操作的时间复杂度为($O(\log N)$)），也可以自定义一个哈希数组进行查找(哈希查找的时间复杂度为($O(1)$))

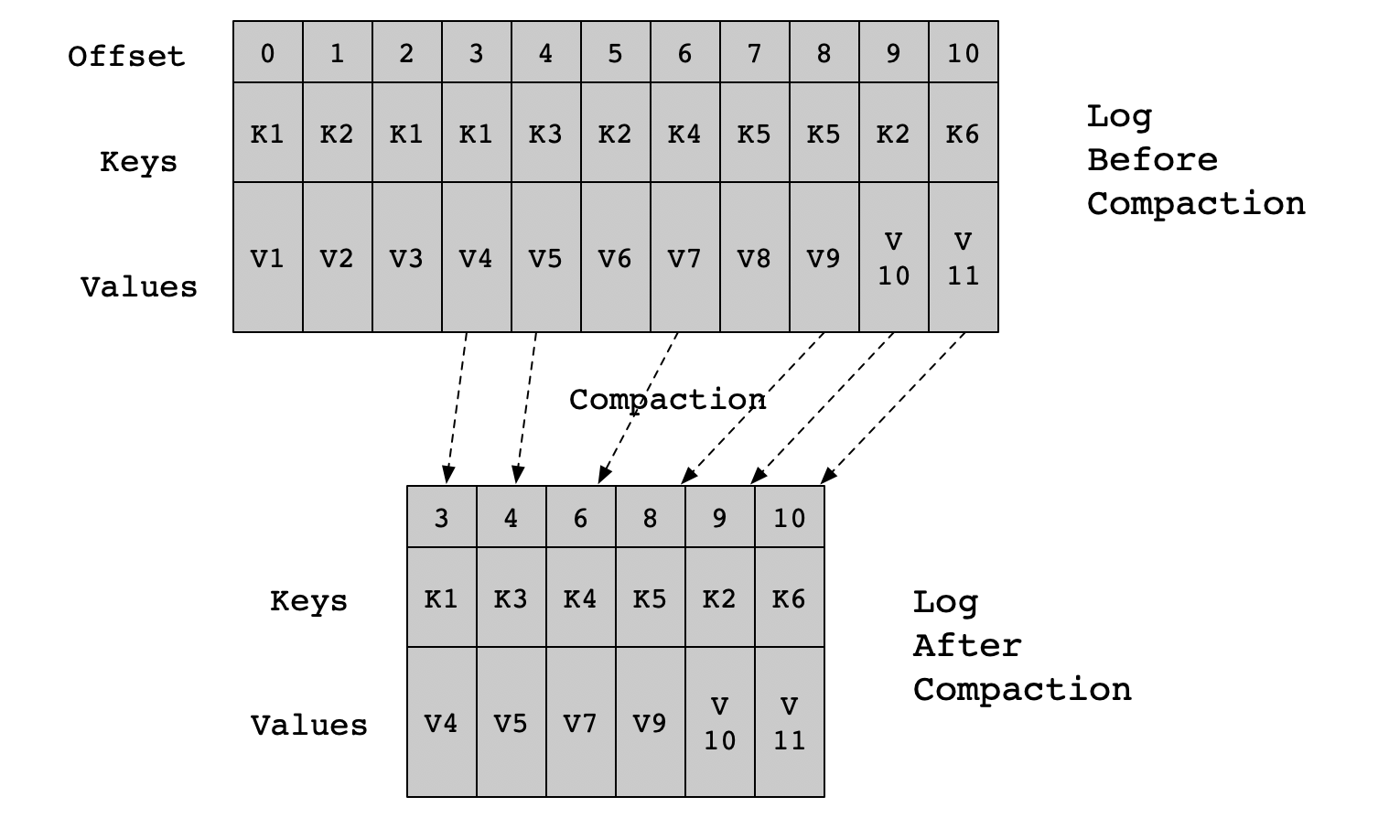
埃氏筛法：对一个给定的范围，求其中的质数，我们从2开始进行遍历，遍历到的每一个数，如果是质数，我们都将其进行添加到数组中，接着对数组中已经记录的所有质数进行乘积，如果得到的结果小于给定的范围，那么就标记这个值为合数，继续遍历下一个数，直到边界时停止。

---

例子：如果我们要求20以内的所有质数，我们首先设定一个标记数组cnt[20]，并令其初值都为0，表示目前的所有数都是一个质数，然后从2开始进行遍历，首先判断2是否是一个质数，可以知道2是一个质数，将2添加到质数数组ans中，然后遍历结果数组，得到2 * 2 = 4 < 20，标记4为一个合数（即：令cnt[4] = 1），接着进入下一个循环，判断3是一个质数，将3添加到ans中，遍历ans，3 * 2 = 6 < 20，标记6为一个合数，3 * 3 = 9 < 20，标记9为一个合数，进入下一个循环，判断4不是一个质数，直接进行遍历ans数组，2 * 4 = 8 < 20，3 * 4 = 12 < 20，4 * 4 = 16 < 20，分别将8，12，16进行标记，表示这些数是一个合数。依次类推知道遍历到最后即可得到所有的质数了（ans数组中记录的即是所有的质数）

GPT的一个解释：

代码：

1. 使用map进行判断是否是纯质数

// 纯质数
#include<iostream>
#include<vector>
#include<map>
#include<string>
using namespace std;
//为了方便找到纯质数，我们需要一个映射 

vector<int> primeNumbers(int lb, int rb){
	vector<int> PN;
	// 定义一个数组，用于标记是否是一个质数
	vector<int> cnt(rb + 10, 0);  // 初始的值设定为0，表示都为质数 
	for(int i = 2;i <= rb;i ++){
		if(!cnt[i]){  // 如果是质数就进行标记，并且添加到数组中
			PN.push_back(i);
			cnt[i] = 1; 
		}
		// 标记出不是质数的数
		for(auto v : PN){
			if(v * i > rb) break;
			cnt[v * i] = 1;  // 首先要判断是否越界
		}
	}
	// 最后得到一个质数的数组PN
	return PN; 
}

// 判单纯质数
map<int, int> smallPrimeNumber = {{2, 1}, {3, 1}, {5, 1}, {7, 1}};
bool purePrimeNumber(int num){
	int temp;
	while(num){
		temp = num % 10;
		if(smallPrimeNumber.find(temp) ==  smallPrimeNumber.end()) return 0;
		num /= 10;
	}
	return 1;
} 
void solve(){
	// leads:首先找到所有的质数，然后再进行寻找所有的纯质数
	const int lb = 1;
	const int rb = 20210605;
	int ans = 0;
	vector<int> ansPN = primeNumbers(lb, rb);
	
	for(auto v : ansPN){
		if(purePrimeNumber(v)) ans++;
	}
	cout<<ans<<endl;
	return ;
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	int t = 1;
	while(t--){
		solve();
	}	
	return 0;
}

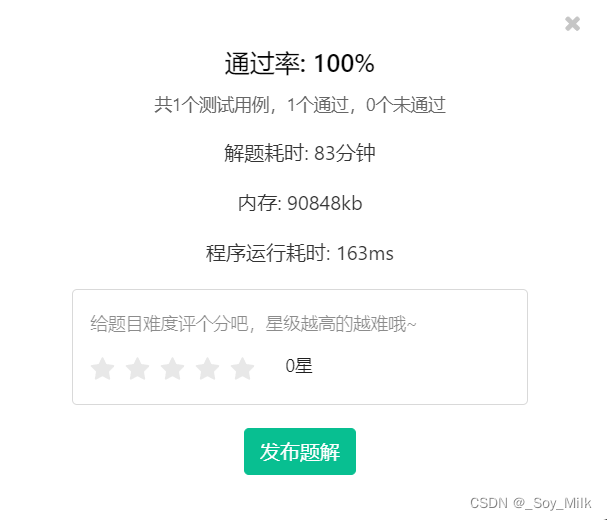
2. 使用一个哈希表判断是否是纯质数

// 纯质数
#include<iostream>
#include<vector>
#include<map>
#include<string>
using namespace std;
//为了方便找到纯质数，我们需要一个映射 
map<int, bool> PPNM; 

vector<int> primeNumbers(int lb, int rb){
	vector<int> PN;
	// 定义一个数组，用于标记是否是一个质数
	vector<int> cnt(rb + 10, 0);  // 初始的值设定为0，表示都为质数 
	for(int i = 2;i <= rb;i ++){
		if(!cnt[i]){  // 如果是质数就进行标记，并且添加到数组中
			PN.push_back(i);
			cnt[i] = 1; 
		}
		// 标记出不是质数的数
		for(auto v : PN){
			if(v * i > rb) break;
			cnt[v * i] = 1;  // 首先要判断是否越界
		}
	}
	// 最后得到一个质数的数组PN
	return PN; 
}

// 判单纯质数
int hashMap[10] = {0, 0, 1, 1, 0, 1, 0 ,1 ,0 ,0};
bool purePrimeNumber(int num){
	int temp;
	while(num){
		temp = num % 10;
		num /= 10;
		if(!hashMap[temp]) return false;
	}
	return true;
}

void solve(){
	// leads:首先找到所有的质数，然后再进行寻找所有的纯质数
	const int lb = 1;
	const int rb = 20210605;
	int ans = 0;
	vector<int> ansPN = primeNumbers(lb, rb);
	
	for(auto v : ansPN){
		if(purePrimeNumber(v)) ans++;
	}
	cout<<ans<<endl;
	return ;
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	int t = 1;
	while(t--){
		solve();
	}	
	return 0;
}