文章目录
- 动态规划的定义
- 动态规划的核心思想
- 青蛙跳阶问题
- 解法一:暴力递归
- 解法二:带备忘录的递归解法(自顶向下)
- 解法三:动态规划(自底向上)
- 动态规划的解题套路
- 什么样的问题考虑使用动态规划?
- 动态规划的解题思路
- 第14届JavaB组蓝桥杯“蜗牛”问题
动态规划的定义
动态规划(Dynamic programming,简称 DP),是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
”dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems.“
动态规划就是给定的一个问题拆成一个个子问题,直到子问题可以直接解决。把子问题答案保存起来,以减少重复计算。再根据子问题答案反推,得出原问题解的一种方法。
动态规划的核心思想
拆分子问题,记住过往,减少重复运算。
体现该思想的例子
- A : “1+1+1+1+1+1+1+1 =?”
- A : “上面等式的值是多少”
- B : 计算 “8”
- A : 在上面等式的左边写上 “1+” 呢?
- A : “此时等式的值为多少”
- B : 很快得出答案 “9”
- A : “你怎么这么快就知道答案了”
- A : “只要在8的基础上加1就行了”
- A : “所以你不用重新计算,因为你记住了第一个等式的值为8!动态规划算法也可以说是 ‘记住求过的解来节省时间’”
青蛙跳阶问题
问题:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法。
问题分析:
到达第10级,可以从第9级跳1级台阶,也可以从第8级跳2级台阶。
到达第9级可以从第8级跳1级台阶,也可以从第7级跳2级台阶。
到达第8级可以从第7级跳1级台阶,也可以从第6级跳2级台阶。
定义f(n)为跳到第n级台阶
f(10) = f(9)+f(8) f (9) = f(8) + f(7) f (8) = f(7) + f(6) ... f(3) = f(2) + f(1) 即通用公式为: f(n) = f(n-1) + f(n-2)
- 当只有2级台阶时,有两种跳法,第一种是直接跳两级,第二种是先跳一级,然后再跳一级。即f(2) = 2;
- 当只有1级台阶时,只有一种跳法,即f(1)= 1;
解法一:暴力递归
class Solution {
public int Ways(int n) {
if(n == 1){
return 1;
}
if(n == 2){
return 2;
}
return Ways(n-1) + Ways(n-2);
}
}
时间复杂度:
- 一个子问题时间 = f(n-1)+f(n-2),也就是一个加法的操作,所以复杂度是 O(1);
- 问题个数 = 递归树节点的总数= 2n-1,所以是复杂度O(2n)。
总结:
- 时间复杂度是指数级别,爆炸式增长,容易超时。
- 存在大量重复计算。
改进措施: 使用备忘录,将计算过的答案存下来。省去重复计算的耗时。
解法二:带备忘录的递归解法(自顶向下)
一般使用一个数组或者一个map集合充当备忘录。
static Map<Integer,Integer> map=new HashMap();
private static int ways2(int n) {
if(n==1) return 1;
if(n==2) return 2;
if(map.containsKey(n)) {
return map.get(n);
}else {
map.put(n,(ways(n-1)+ways(n-2)));
return ways(n-1)+ways(n-2);
}
}
时间复杂度:
子问题个数=树节点数=n,解决一个子问题还是O(1),所以带备忘录的递归算法的时间复杂度是O(n)。
解法三:动态规划(自底向上)
动态规划和带备忘录的递归解法基本思想是一致的,都是减少重复计算,时间复杂度也都是差不多。
- 带备忘录的递归,是从f(10)往f(1)方向延伸求解的,所以也称为自顶向下的解法。
- 动态规划从较小问题的解,由交叠性质,逐步决策出较大问题的解,它是从f(1)往f(10)方向,往上推求解,所以称为自底向上的解法。
动态规划有几个典型特征,最优子结构、状态转移方程、边界、重叠子问题。
在青蛙跳阶问题中:
- f(n-1)和f(n-2) 称为 f(n) 的最优子结构
- f(n)= f(n-1)+f(n-2) 称为状态转移方程
- f(1) = 1, f(2) = 2 是边界
- 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)是重叠子问题。
我们来看下自底向上的解法,从f(1)往f(10)方向,一个for循环就可以解决
private static int ways(int n) {
if(n==1) return 1;
if(n==2) return 2;
int a=1,b=2,temp=0;
for(int i=3;i<=n;i++) {
temp=a+b;
a=b;
b=temp;
}
return temp;
}
动态规划的解题套路
什么样的问题考虑使用动态规划?
如果一个问题,可以把所有可能的答案穷举出来,并且穷举出来后,发现存在重叠子问题,就可以考虑使用动态规划。
比如一些求最值的场景,如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等,都是动态规划的经典应用场景。
动态规划的解题思路
动态规划的核心思想就是拆分子问题,记住过往,减少重复计算。 并且动态规划一般都是自底向上的,动态规划的思路如下:
- 穷举分析
- 确定边界
- 找出规律,确定最优子结构
- 写出状态转移方程
★ 一道动态规划问题,其实就是一个递推问题。假设当前决策结果是f(n),则最优子结构就是要让 f(n-k) 最优,最优子结构性质就是能让转移到n的状态是最优的,并且与后面的决策没有关系,即让后面的决策安心地使用前面的局部最优解的一种性质。
第14届JavaB组蓝桥杯“蜗牛”问题
问题描述:
这天,一只蜗牛来到了二维坐标系的原点。 在 x 轴上长有 n 根竹竿。它们平行于 y 轴,底部纵坐标为 0,横坐标分别为 x1, x2,…, xn。竹竿的高度均为无限高,宽度可忽略。蜗牛想要从原点走到第 n 个竹竿的底部也就是坐标 (xn, 0)。它只能在 x轴上或者竹竿上爬行,在 x 轴上爬行速度为 1 单位每秒;由于受到引力影响,蜗牛在竹竿上向上和向下爬行的速度分别为 0.7 单位每秒和1.3 单位每秒。 为了快速到达目的地,它施展了魔法,在第 i 和 i + 1 根竹竿之间建立了传送门(0 < i < n),如果蜗牛位于第 i 根竹竿的高度为 ai 的位置 (xi , ai),就可以瞬间到达第 i + 1 根竹竿的高度为 bi+1 的位置 (xi+1,bi+1),请计算蜗牛最少需要多少秒才能到达目的地。 输入格式 输入共 1 + n 行,第一行为一个正整数 n; 第二行为 n 个正整数x1, x2, . . . , xn; 后面 n − 1 行,每行两个正整数 ai , bi+1。
输入格式
3
1 10 11
1 1
2 1
输出格式
4.20
样例说明
(0, 0) → (1, 0) → (1, 1) → (10, 1) → (10, 0) → (11, 0),花费时间为 1+1/0.7+0+1/1.3+1 ≈ 4.20
评测用例规模与约定
对于 20% 的数据,保证 n ≤ 15;
对于 100% 的数据,保证 n ≤ 105,ai , bi ≤ 104,xi ≤ 109
问题分析
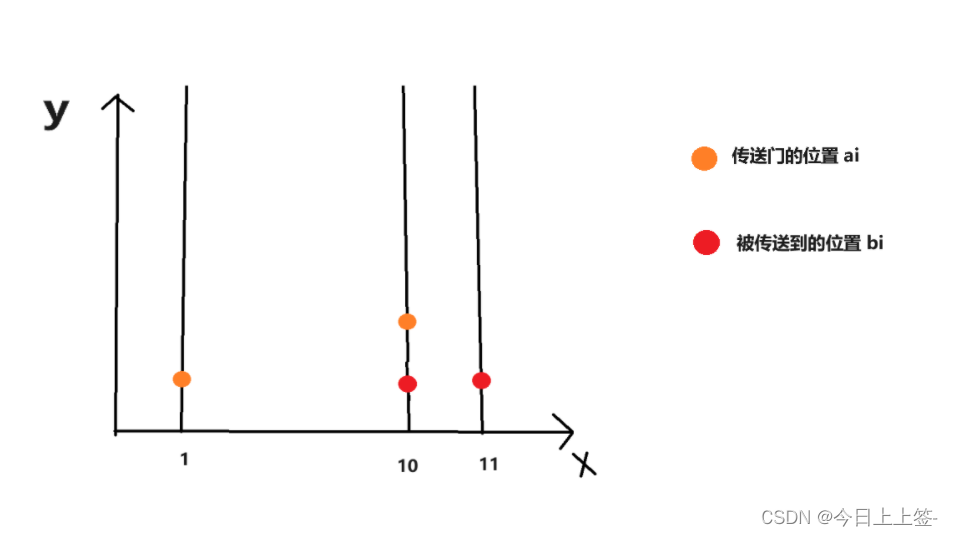
每根竹竿有两个出发点,从最底部出发和从传送门出发。自底而上,每次选取最短的路径。
采用动态规划
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//输入有几根竹竿
int n = sc.nextInt();
//将n个竹竿的横坐标存放在一个数组gan中.
//为了方便,0舍弃不用
int[] gan = new int[n + 1];
for (int i = 1; i <= n; i++) {
gan[i] = sc.nextInt();
}
//存放每个下标对应竹竿的传送门位置 ai
int[] a = new int[n + 1];
//存放每个下标对应的传送到的位置 bi+1
int[] b = new int[n + 1];
//为了方便,0舍弃不用。最后一根竹竿不需要设置传送门a
for (int i = 1; i < n; i++) {
a[i] = sc.nextInt();
b[i + 1] = sc.nextInt();
}
//新建一个二维数组用来存放,从每个竹竿有两个出发点出发,同样舍弃[0][0],[0][1]不用
double[][] dp = new double[n + 1][2];
//第一根竹竿出发点有两个
dp[1][0] = gan[1];
dp[1][1] = gan[1] + a[1] / 0.7;
//每行二维数组的第一个数存放从上一根竹竿的两个出发点出发到达这根竹竿底部的路径长短,
// 第二个数存放从上一根竹竿的两个出发点出发到达这根竹竿传送门的路径长短
for (int i = 2; i < n + 1; i++) {
dp[i][0] = Math.min((dp[i - 1][0] + gan[i] - gan[i - 1]), (dp[i - 1][1] + b[i] / 1.3));
//如果此竹竿的传送门比传送过来的位置高,则第二种出发点需要往上爬 对应/0.7
if (a[i] > b[i]) {
dp[i][1] = Math.min((dp[i - 1][0] + gan[i] - gan[i - 1] + a[i] / 0.7), (dp[i - 1][1] + (a[i] - b[i]) / 0.7));
} else {
dp[i][1] = Math.min((dp[i - 1][0] + gan[i] - gan[i - 1] + a[i] / 0.7), (dp[i - 1][1] + (b[i] - a[i]) / 1.3));
}
}
System.out.printf("%.2f", dp[n][0]);
}
}