题目描述

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。

示例 1：

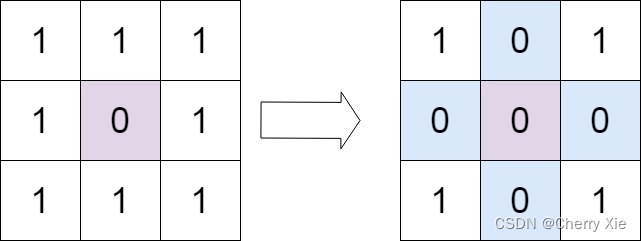
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]
示例 2：

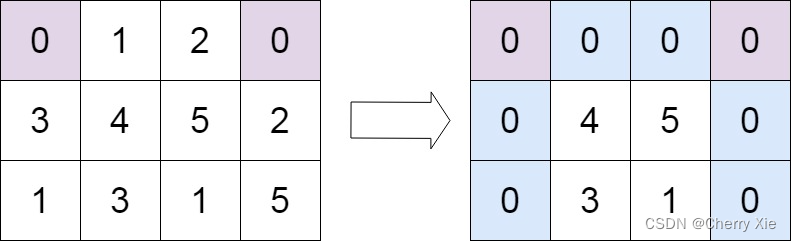
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -231 <= matrix[i][j] <= 231 - 1

进阶：

• 一个直观的解决方案是使用 O(mn) 的额外空间，但这并不是一个好的解决方案。
• 一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
• 你能想出一个仅使用常量空间的解决方案吗？

思路

根据题目描述，我们可以了解到：
1、遍历矩阵每一行，有0的行元素全部置零。
2、出现零的位置，即当前行的这个位置出现零，其他行的这个位置也得置零。
3、根据第一次遍历，我们可以得到哪些元素需要置零，剩下的便是开始置零：
（1）如果不考虑时间，可以直接第一时间替换，同时去重复
（2）如果考虑时间，那边可以先记录需要置零的位置，显然我们可以确保其不重复

OK，思考完毕，开整！

空间换时间解法

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        row = len(matrix)
        col = len(matrix[0])
        row_zero = set()
        col_zero = set()
        for i in range(row):
            for j in range(col):
                if matrix[i][j] == 0:
                    row_zero.add(i)
                    col_zero.add(j)
                    
        for i in range(row):
            for j in range(col):
                if i in row_zero or j in col_zero:
                    matrix[i][j] = 0