问题描述

什么是最大团？最大团的定义？

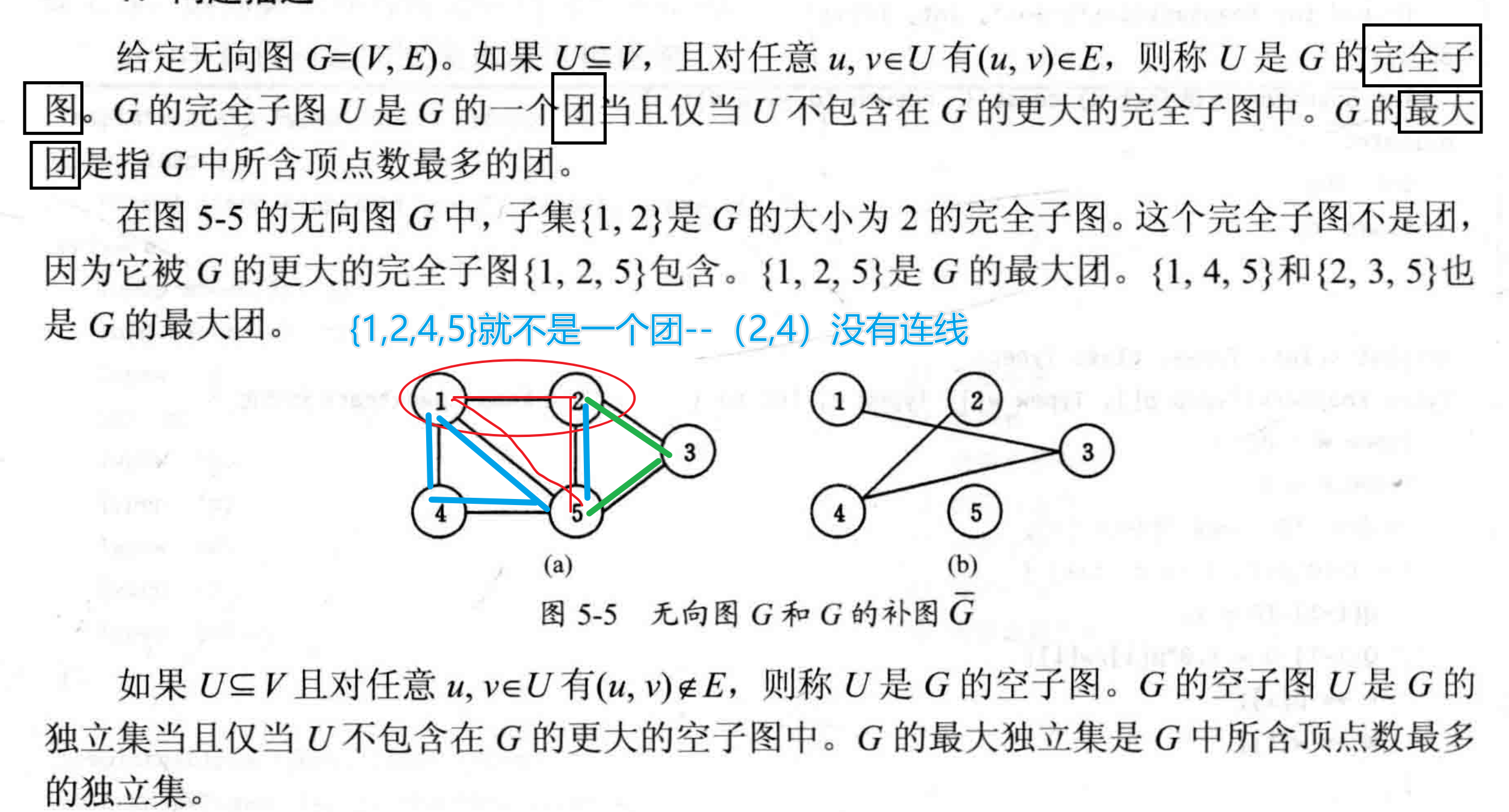
完全图：如果无向图中的任何一对顶点之间都有一条边，这种无向图称为完全图。

完全子图：给定无向图G=(V,E)。如果U⊆V，且对任意u，v⊆U 有(u，v) ⊆ E，则称U 是G 的完全子图。

团（最大完全子图）: U是G的团当且仅当U不包含在G 的更大的完全子图中

最大团：G 的最大团是指G中所含顶点数最多的团。

空子图：给定无向图G=(V,E)。如果U⊆V，且对任意u，v⊆U 有(u，v) ∉ E，则称U 是G 的空子图。G的空子图U是G的独立集当且仅当U不包含在G的更大空子图中。

独立集：对于给定无向图G=(V,E)。如果顶点集合V*⊆V，若V*中任何两个顶点均不相邻，则称V*为G的点独立集，或简称独立集。

最大独立集：G中所含顶点数最多的独立集。

无向图G的最大团问题和最大独立集问题都可以用回溯法在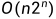 $\text{[math]}$ 的时间内解决。

图G的最大团问题可以看做是图G的顶点集V的子集选取问题

回溯法有两种模板--子集树和排列树。最大团问题就可以用子集树来表示问题的解空间。

问题分析

设当前扩展节点Z位于解空间树的第i层，进入左子树前（选取这个点i），必须确认从点i到已经选入的点集中的每一个点都有边相连。进入右子树前（不选择这个点i），必须确认还有足够多的可以选择的点，使得有可能在右子树中找到更大的团。

详细描述

思路：首先设最大团为一个空团，往其中加入一个顶点，然后依次考虑每个顶点，查看该顶点加入团之后仍然构成一个团，如果可以，考虑将该顶点加入团，或者舍弃两种情况，如果不行，直接舍弃，然后递归判断下一顶点。对于无连接或者直接舍弃两种情况，在递归前，可采用剪枝策略来避免无效搜索。

判断条件：为了判断当前顶点加入团之后是否仍是一个团，只需要考虑该顶点和团中顶点是否都有连接。

剪枝策略：如果剩余未考虑的顶点数加上团中顶点数不大于当前解的顶点数，可停止继续深度搜索，否则继续深度递归。

书上的伪代码是这样的：

首先定义一下初始的变量

回溯主函数：

还是很有回溯框架--子集树模板的样子，思考清楚进入左子树和进入右子树的条件，剪枝，（单层遍历逻辑）就可以轻而易举拿下了。

//最大团问题
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int maxnum = 101;
bool a[maxnum][maxnum]; //图的邻接矩阵
bool x[maxnum];         //当前解
int cn;                 //当前团的顶点数
int bestn;              //当前的最优解
int n;                  //图G的顶点数
int e;                  //图G的边数
void display(){
    for (int j = 1; j <= n; j++){
        if (x[j] == true) printf("%d ", j);
    }
    printf("\n");
}
void backtrack(int i){
    int j;
    if (i > n)//到达叶子节点
    {
        bestn = cn;//更新最优值
        printf("%d\n", bestn);//输出详细的信息
        display();
        return;
    }
    bool ok = true;
    for (j = 1; j < i; j++){
        if (x[j] && !a[j][i]) {// i与j不相连
            ok = false;
            break;
        }
    }
    //检查是否这个点与其他所有顶点都有边相连，符合条件，进入左子树
    if (ok){
        cn++;
        x[i] = true;
        backtrack(i + 1);//检查下一个顶点
        cn--;//还原现场
    }
    if (cn + n - i > bestn) //剪枝
    {
        x[i] = false;
        backtrack(i + 1);
    }
}

int main(){
    int i, u, v;
    //初始化
    memset(a, false, sizeof(a));
    memset(x, false, sizeof(x));
    scanf("%d%d", &n, &e); // 定点数，边数
    for (i = 0; i < e; i++)
    {
        scanf("%d%d", &u, &v);
        a[u][v] = true;
        a[v][u] = true;
    }
    cn = bestn = 0;
    backtrack(1);
    return 0;
}

/*
5 7
1 2
1 4
1 5
2 5
2 3
3 5
4 5
*/

又是一道回溯法的题目，和最优装载这个问题及其相似