题目
1700:八皇后问题
总时间限制: 10000ms 内存限制: 65536kB
描述
在国际象棋棋盘上放置八个皇后,要求每两个皇后之间不能直接吃掉对方。
输入
无输入。
输出
按给定顺序和格式输出所有八皇后问题的解(见Sample Output)。
样例输入
样例输出
No. 1
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
No. 2
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 1 0 0 0 0 0
No. 3
1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0
No. 4
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
No. 5
0 0 0 0 0 1 0 0
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
No. 6
0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0
No. 7
0 0 0 0 1 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0
No. 8
0 0 1 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
No. 9
0 0 0 0 1 0 0 0
1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0
…以下省略
提示
此题可使用函数递归调用的方法求解。
理解
1每一列都要尝试放置到每一行,
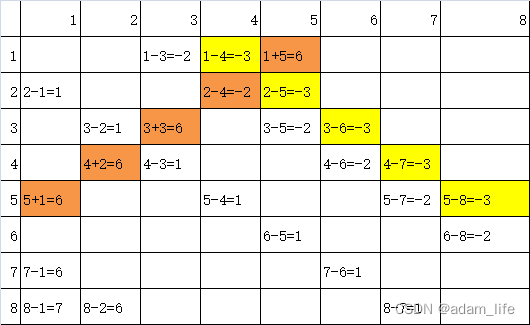
2只要该行、该斜行(行加列)、该反斜行(8+行-列)没标记就可以放置皇后
3标记放置该行、该斜行、该反斜行
4然后在下列递归
5直到能到达9就完成8皇后的放置,输出,并结束该次
6回溯,撤销该列行放置操作,该尝试下一行。
代码
#include <bits/stdc++.h>
using namespace std;
int m=1;
bool k[9][9],//皇后的位置
h[9],//某列有没有皇后
xk[16],//某斜列有没有皇后,8+行-列
fx[16];//某反斜列有没有皇后,行+列
void view(int x){
cout<<"No. “<<x<<endl;
for(int i=1;i<=8;i++){
for(int j=1;j<=8;j++)cout<<k[i][j]<<” ";
cout<<endl;
}
}
void go(int x){//几列
if(x==9){view(m++);return;}//8列都有皇后,就可以输出,并结束该方案
for(int i=1;i<=8;i++)//几行
if(!h[i]&&!fx[8+i-x]&&!xk[i+x]){//如果该行,反斜,斜都没有皇后
k[i][x]=1,h[i]=1,xk[i+x]=1,fx[8+i-x]=1;//i行x列设置皇后
go(x+1);//设置下列皇后
k[i][x]=0,h[i]=0,xk[i+x]=0,fx[8+i-x]=0;//回溯,撤销该列i行的皇后放置,改到i+1行
}
}
int main(){
go(1);//从1列开始
return 0;
}
小结
深搜,回溯,
能有符合条件的8列就可以,
否则撤销,尝试下一行。
没有上下左右搜索,
而是每列每行搜索。