一维数组不想更了，弄点二维数组！ 

1.新矩阵

思路

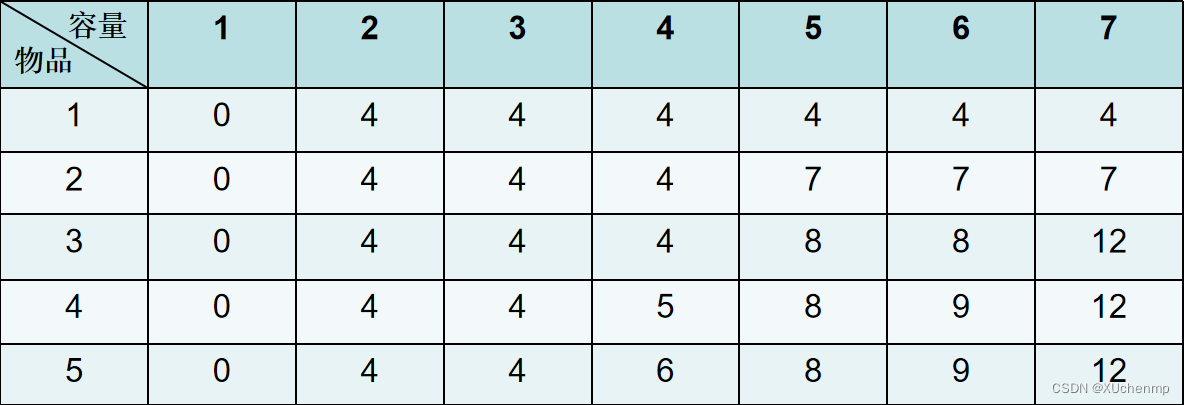
题目简单，6*6=36，可以得知有36个元素。数组就定义成a[7][7]，难点在与如何找出对角线上的元素。可以画图分析：

通过观察不难发现，元素1，可以表示为：i==j，那么对角线的特征就找到了，是循环i==j的时候就a[i][j]+=10；对角线还有一个特征：i+j==7，当这两个都出现的或者只出现一个特性的都是对角线上的元素。

 stew()函数

在做一些特殊题目是可能要用到stew()函数，stew函数有什么用呢？它的作用是控制输出长宽，可以用它来控制输出字符与空格，在二维数组的题目里经常用，例如：稀疏矩阵，杨辉三角.....都会用到，在字符串和字符数组中也十分常用！在这里我们不做深入探究毕竟它在打竞赛时很少出现！当然如果你想要用stew()函数就要声明该库：

#include<iomanip>

AC代码：

#include<iostream>
#include<iomanip>
using namespace std;//先声名一下，我是觉得可有可无！
int a[7][7];
int main(){
    for(int i=1;i<=6;i++){
        for(int j=1;j<=6;j++){
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=6;i++){
        for(int j=1;j<=6;j++){
            if(i+j==7||i==j){
                a[i][j]+=10;
            }
        }
    }
    for(int i=1;i<=6;i++){
        for(int j=1;j<=6;j++){
            cout<<stew(5)<<a[i][j];
            cout<<endl;
        }
    }
    return 0;
}

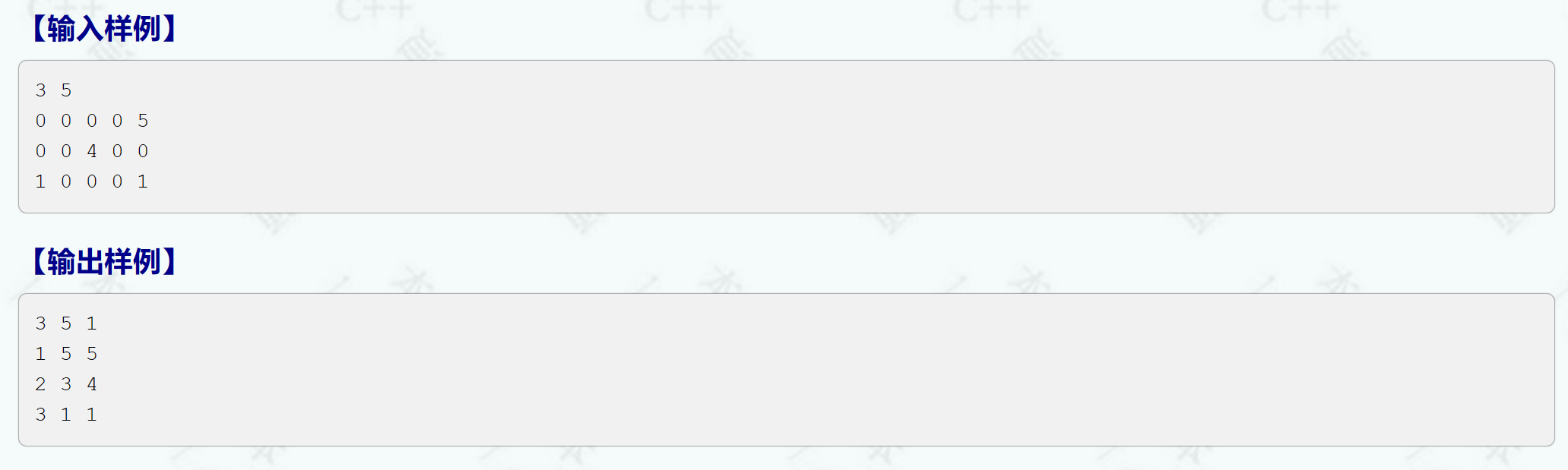
 2.稀疏矩阵

 思路

我们可以定义两个数组，一个a[4][6],一个b[102][4]。先读入a数组，然后我们可以定义一个变量k。当找到非0值的时候，就把k累加起来。那么k开始时是0，现在加1，表示第一行。每次累加都代表第几行。

总之，这题就是要找到非零值并且记忆位置，将原始矩阵存入a数组，再将转化后的矩阵传入b数组

AC代码：

#include<iostream>
#include<iomanip>
coust int n=3,m=5;
int a[n+1][m+1],b[101][4],k=0;
using namespace std;
int main(){
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(a[i][j]!=0){
                k++;
                b[k][1]=i;//i是行号
                b[k][2]=j;//j是列号
                b[k][3]=a[i]a[j];//元素
            }    
        }
    }
    for(int i=1;i<=k;i++){
        for(int j=1;j<=3;j++){
            cout<<stew(3)<<a[i][j];
            cout<<endl;
        }
    }
    return 0;
}